中学数学「連立方程式」の効果的な教え方③ 代入法

中２数学「連立方程式」の教え方、３回目です。

今回は代入法の教え方。

ここでつまずいている中学生にどう教えたらいいか、具体的な指導方法を載せるので参考にしてください。

[前の記事]中２数学「連立方程式」② 加減法

[次の記事]中２数学「連立方程式」④ 小数、分数

（数学指導法の記事一覧はまとめページへ）

前回までの記事の復習

いちおう、前回までのかんたんな復習をしておきます。

などがありました。

そして、連立方程式の指導順は

1. 復習をする（1次方程式、代入、式の加減）
2. 連立方程式とは何かの説明
3. 加減法の導入（たし算）
4. 加減法の導入（ひき算）
5. 加減法つづき（一方だけ係数をそろえる）
6. 加減法つづき（両方とも係数をそろえる）
7. 加減法まとめ

という7段階が、導入から加減法まででした。

今回はその続きとして、

8. 代入法の導入（\(y=\)単項式）
9. 代入法の導入（\(x=\)単項式）
10. 代入法つづき（多項式の場合）
11. 代入法の発展とまとめ

という4段階を、以下、くわしく解説していきます。

[関連記事]

• 中２「式による説明」
• 中２「連立方程式の文章題」①

 

代入法の導入（\(y=\)単項式）

さて、前回まで加減法という解き方を習ってきた。

しかし連立方程式には、もうひとつ解き方がある。

それが「代入法」だ。

解答を示してから、解説

\begin{eqnarray} \left\{ \begin{array}{l} y = 2x \ \large{\mbox{…①}} \\ 3x+y = 5 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}

この連立方程式の問題、①が \(y=2x\) の形になっている。

つまり \(y\) の正体は \(2x\) と言っている。

じゃ、②式の \(y\) のところ、代わりに \(2x\) にしてもいいよね。

つまり②式に \(y=2x\) を代入できるよね。

何をしたかわかるね。

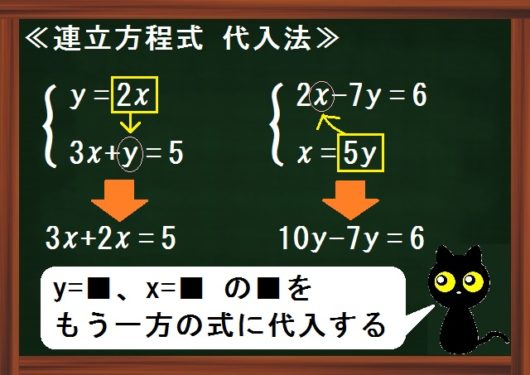
ようするに、\(y=\)■（または \(x=\)■ ）という形がどっちかにあれば、その■をもう一方の式に代入する。

そうしたら文字は1種類だけになるから、それを解く。

あとは加減法のときと同じ。

これが代入法の解き方だ。

 

書き写させてから、類題

理解したら、書き写そう。

書き写すときの注意点は加減法のときと同じ。

• どんな計算をしたのか、ことばを必ず書く。
• 式どうしの筆算のときや方程式を解くとき、＝を縦にそろえるときれい。
• 答えの形は教科書によっては \((x,y)=(1,2)\) などの場合もある。学校に従うこと。

何よりも、人に見せてもわかりやすい解答を書くことが大事やで。

書き写せたら、類題を解いてみよう。

\begin{eqnarray} \left\{ \begin{array}{l} 5x-y=-2 \\ y=4x \end{array} \right.\end{eqnarray}

（解答は\(x=-2,y=-8\) ）

（めんどいので途中式省略。生徒は必ず書くこと）

＞Amazonプライム・ビデオ『博士の愛した数式』

 

代入法の導入（\(x=\)単項式）

もちろん、\(y=\)●の形ばかりじゃない。

\(x=\)●の形もあるぞ。

解答を示してから、解説

\begin{eqnarray} \left\{ \begin{array}{l} 2x-7y=6 \ \large{\mbox{…①}} \\ x=5y \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}

これはこう解きます。

つまり、\(2x-7y=6\) の \(x\) を \(5y\) に入れかえたんだ。

ここで注意せなあかんのは、\(2\) と \(x\) ってかけ算でつながってるってこと。

だから代入したら \(2 \times 5y\) で、先頭は \(10y\) になる。

たまに足し算と勘違いする人がいるから、気をつけて。

 

書き写させてから、類題

もうひとつ、書き写しながら聞いてくれ。

学校によっては、こう書く先生もいる↓

最初の一行目、必要だと思う？

うん、おれもいらないと思う。

暗算でいけるやん。

つまり代入するのが単項式なら、かけ算は暗算でやってしまえばいいんだ。

一行目を書くことでよけいにごちゃごちゃするからね。

…では、類題。

\begin{eqnarray} \left\{ \begin{array}{l} x=-2y \\ 3x+y=5 \end{array} \right.\end{eqnarray}

（解答は\(x=2,y=-1\) ）

＞Amazonプライム・ビデオ『奇蹟がくれた数式(字幕版)』

 

代入法つづき（多項式の場合）

つづいて、多項式を代入する場合。

解答を示してから、解説

\begin{eqnarray} \left\{ \begin{array}{l} 8x-3y=9 \ \large{\mbox{…①}} \\ y=2x-1 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}

こんな問題のように、多項式を代入する場合は、代入したあとの式をちゃんと書いたほうがいい。

このように↓

つまり多項式を代入する際には、かっこをつけてあげること。

これがポイント。

 

書き写させてから、類題

たまーに、10人に1人くらい、多項式を代入するときにも暗算でやろうとする中学生がいる。

つまり \(8x-3(2x-1) = 9\) を書かずに

いきなり \(8x-6x+3 = 9\) と書こうとする人。

そういう生徒はだいたい \(8x-6x-3 = 9\) と間違えます。

だから数学の偏差値が70以下の生徒は、かっこをつけて代入した式を書くべきです。

もしあなたが、あるいは今教えている生徒が、全国模試でトップ層の成績なら、暗算でやってもよしとしましょう。

それ以外の生徒はちゃんとかっこを書きましょう。

…では、類題。

\begin{eqnarray} \left\{ \begin{array}{l} 2x-3y=5 \\ x=2y+4 \end{array} \right.\end{eqnarray}

（解答は\(x=-2,y=-3\) ）

＞Amazonプライム・ビデオ『真夏の方程式』

 

代入法の発展とまとめ

最後に、代入法の発展問題を紹介します。

代入法の発展問題

\begin{eqnarray} \left\{ \begin{array}{l} 3x+2y=17 \\ 2y=x+5 \end{array} \right.\end{eqnarray}

この連立方程式を代入法で解け、と言われたら、解き方は２つある。

この解き方は、②式をムリヤリ \(x=\)～ の形に変形してから代入したものです。

①式②式を見たときに、係数が１の文字が②の \(x\) だけだったので、そうしました。

こんなやり方もある、ということね。

んで、もうひとつの解き方はこう↓

この解き方は、\(2y\) の代わりに \(x+5\) をそのまま放りこんだものです。

①式に \(+2y\) があって、②式が \(2y=\)～ の形だったから、たまたまうまくいった。

こんな問題のように、たまたまうまくいく場合もある。

連立方程式を解くときは、まず問題の形をよく観察すること。

そしてどの方法で解けばいちばんラクできるかと、悩むこと。

こういう考え方を常にするようになると、連立方程式を解くのが得意になります。

 

まとめ

以上、代入法の解き方でした。

まとめると、

• \(y=\)～ , \(x=\)～ の形があったら代入して解けばいい。
• ～部分が多項式の場合は、かっこをつけて代入すること。
• \(y=\)～ , \(x=\)～ の形に変形してもっていけば、代入法は使える。
• たまに \(2y=\)～ 等のままでうまく代入できる場合がある。問題をよく見ること。

という４点がコツです。

 

さて、ここまでで連立方程式の解き方は「加減法」「代入法」と両方出そろった。

では仕上げに、以下の連立方程式を、加減法と代入法、両方の解き方で解いてみよう。

\begin{eqnarray} \left\{ \begin{array}{l} 3x+2y=-1 \\ x-3y=-15 \end{array} \right.\end{eqnarray}

あなたはどっちの解き方がいいと思う？

加減法？それとも代入法？

そう思った理由は？

連立方程式に限らずだけど、つねにこういう思考を頭の中でするといい。

もういちど言う。

連立方程式を解くときは、まず問題の形をよく観察すること。

そしてどの方法で解けばいちばんラクできるかと、悩むこと。

次回の応用問題でも、この心がけを忘れないように。

→中学数学「連立方程式」の効果的な教え方④ 小数・分数問題