中学数学「連立方程式」の効果的な教え方② 加減法のつづき

前回につづいて、中２数学「連立方程式」の教え方です。

わたしの考えるもっとも効率的な指導とは以下の順番でした。(導入～加減法まで)

1. 復習をする（1次方程式、代入、式の加減）
2. 連立方程式とは何かの説明
3. 加減法の導入（たし算）
4. 加減法の導入（ひき算）
5. 加減法つづき（一方だけ係数をそろえる）
6. 加減法つづき（両方とも係数をそろえる）
7. まとめ

今回は 4.加減法の導入（ひき算）からになります。

前回同様、ムダな指導は一切省いて、まず解答を示す→解説する→書き写させる→類題 という指導順でいきます。

連立方程式の指導に不安のある方はぜひ参考ください。

[前の記事]中２数学「連立方程式」導入

[次の記事]中２数学「連立方程式」代入法

（数学指導法の記事一覧はまとめページへ）

4.加減法の導入（ひき算）

では、以下の問題はどうやって解いたらいいだろう。

解答を示してから、解説

\begin{eqnarray} \left\{ \begin{array}{l} 7x+3y = 13 \\ 5x+3y = 11 \end{array} \right.\end{eqnarray}

こうやって解きます。

 

何をしたか、もうわかるね。

今度は式どうしをひき算したんだ。

なぜならこの問題は \(y\) の係数が数字も符号も同じだったから。

あとは前回と同様。

\(x=\)○ と出して、それを①式あるいは②式に代入して \(y\) も出す。

このように、加減法とは名前のとおり、式どうしを足したり引いたりして一方の文字をまず消去する方法です。

足すか引くかは、係数の、

• 数字が同じで符号が逆→たし算
• 数字も符号も同じ→ひき算

で判断しよう。

[前の記事] 「連立方程式」① 導入

 

書き写させてから、類題

理解したら、また書き写してもらう。

書き写すときの注意点はやはり３つ。

• どんな計算をしたのか、ことばを必ず書く。
• 式どうしの筆算のときや方程式を解くとき、＝を縦にそろえるときれい。
• 答えの形は教科書によっては \((x,y)=(2,4)\) などの場合もある。学校に従おう。

いいかい、ここで大事なのは人が見てもわかりやすい解答を書くことだ。

この「人が見てわかりやすい解答」を書けるかどうかで、これからも数学が得意になるかどうか決まるといっても過言じゃない。

ゆっくりでいいから、正確に書き写して。

 

では、類題を一緒に解いてみよう。

\begin{eqnarray} \left\{ \begin{array}{l} x-4y= 8 \\ 3x-4y = 0 \end{array} \right.\end{eqnarray}

 

指導上の注意点

ここまでで、指導者の方には４つ注意していただきたい点があります。

１つ。生徒がきちんと書き写せているかを見て、適宜指導を入れること。

２つ。類題を一緒に解く際には、\(x=\)○ と出た時点で「①と②どっちに代入する？」と発問し、生徒自身に考えさせる割合を増やしていくこと。

３つ。このあと \(x\) の係数がそろっている問題も出して、先に \(x\) が消える場合もあると示すこと。つまり、\begin{eqnarray} \left\{ \begin{array}{l} 2x+6y= -2 \\ 2x+3y = -1 \end{array} \right.\end{eqnarray} \begin{eqnarray} \left\{ \begin{array}{l} -8y+y= 1 \\ -8x-3y = -28 \end{array} \right.\end{eqnarray} などの問題です。
（答えは \(x=2 , y=-1\) と \(x=\frac{3}{4} , y=7\)）

４つ。最後に「答えの確かめができる」と示すこと。つまり出た答えの組を、代入していないほうの式に代入して、両辺が＝になるか。この確かめができると示すことでミスは少なくなります。

以上を終えたら、練習問題をさせてあげてください。

 

5.加減法つづき(一方だけ係数をそろえる)

つづいて、加減法の発展バージョン。

係数がそろってない問題の連立方程式の教え方を見ていきます。

解答を示してから、解説

\begin{eqnarray} \left\{ \begin{array}{l} 7x+6y = 8 \ \large{\mbox{…①}} \\ 2x+3y = 1 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}

この連立方程式の問題は、\(x\) の係数も \(y\) の係数もちがう。

だからこのままじゃ足しても引いても文字が消えない。

どうすればいいか？

\(6\) と \(3\) という \(y\) の係数に注目。

\(3\) を２倍すれば \(6\) だ。

だから②の式を２倍してやればいいんだ！

 

解答は以上のように書く。

つまり、まず②×２をして、その式を②’とすること。

そんで①と②’を筆算して、文字をひとつ消す。

あとは同じだ。③を①または②に代入してもう一方も出す。

これが、係数がそろっていない場合の連立方程式の解き方。

ようするに、係数をタテに見比べて、「上が下の２倍だ」とか「下が上の３倍だ」とかを発見すればいいわけ。

 

書き写させてから、類題

では解答を書き写して。

書き写しながら、耳だけ聞いてくれ。

何倍かするときは、必ず両辺にかけること。

左だけ、右だけ２倍しちゃうことがあるから注意して。

また、③の値は、②’に代入してもいい。

ただ元の①あるいは②に代入したほうが計算はかんたんだ。

何倍かしたあとの式は数字がでっかくなっちゃってるからね。

 

よし、書けたら類題を一緒に解こう。

\begin{eqnarray} \left\{ \begin{array}{l} 3x-2y= 8 \\ -7x+8y = -2 \end{array} \right.\end{eqnarray}

 

指導上の注意点

ここでも指導者は以下４つを注意してください。

1. ちゃんと書き写せているか手元を見る
2. 一緒に解く際には発問して生徒に考えさせる
3. このあと \(x\) の係数をそろえる問題も出す
4. 答えの確かめを示す

2.に関して、この段階からわたしは発問を増やします。

「\(x\) と \(y\) 、どっちの係数をそろえたらいい？」
「①と②、どっちを何倍する？」
「足し算と引き算、どっちしたらいい？」
「\(x=6\) は①と②どっちに代入する？」

とくにこの４つは必ずおこなう発問です。

生徒が自力でできるようになるために、こうした「判断ポイントでの発問」「応答が一言で済む発問」を、ジュウゴはつねに心がけています。参考になれば。

以上を終えたら、練習問題をさせてあげてください。

[関連記事]
「連立方程式」文章題① 立式のコツ

 

6.加減法つづき(両方とも係数をそろえる)

もうひとつ、加減法の発展バージョン。

これを終えたら連立方程式の加減法はおしまいです。

解答を示してから、解説

\begin{eqnarray} \left\{ \begin{array}{l} 5x-2y = 6 \ \large{\mbox{…①}} \\ 4x-3y = -5 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}

この連立方程式も、\(x\) の係数、\(y\) の係数ともにちがう。

そしてタテに見比べたとき、どっちかがどっちかの何倍になって……ない。

じゃあどうすればいいか？

たとえば、こう解きます。

あるいは、こう解きます。

つまり、前者の解き方は
\(y\) の係数 \(2 , 3\) を→ \(6\) にそろえた。

後者の解き方は
\(x\) の係数 \(5 , 4\) を→ \(20\) にそろえた。

このように、\(x\) か \(y\) の係数をそろえるために①②両方をそれぞれ何倍かする。

これが加減法の基本における、最後の知識だ。

 

書き写させてから、類題

じゃ、理解したら書き写して。

そのあいだ、耳だけ貸して。

この問題、\(x\) と \(y\) どっちの係数をそろえたほうが計算がラクかな。

うん、わたしも \(y\) のほうだと思う。

20より６のほうが数字が小さいもんね。

加減法のこういう問題では、「どっちの係数をそろえたほうが数字が小さくなるかな」と考えてから、より計算のラクなほうを選ぼう。ミスが減るよ。

 

では類題を一緒に解こう。

\begin{eqnarray} \left\{ \begin{array}{l} 8x-4y= 32 \\ 7x+6y = 9 \end{array} \right.\end{eqnarray}

 

指導上の注意点

「\(x\) と \(y\) 、どっちの係数をそろえる？」
「\(4 , 6\) をいくつにそろえる？」
「①×いくら？ ②×いくら？」
「足し算？or 引き算？」

など、ここでもやはり発問で生徒自身に考えさせましょう。

特に発問することで \(4 , 6\) を→ \(24\) にそろえる、というミスを防ぐことができます。そういう応答があったら、最小公倍数でそろえると指導してください。

（最小公倍数がパッと思い浮かばない生徒には以下の記事を参照）
中学数学「文字と式」でつまずく原因と解決法②
＊記事内の「途中式が書けない・分数計算ができない」項目の「注意点」に、最小公倍数の教え方があります。

 

また、きちんと書き写せているかの手元確認も、やはり大切です。

この段階でかなり解答が長くなるので、「③を②に代入して」ということばを書かなかったり、方程式の計算を余白にちいさく書いていたりする中学生はけっこういます。

記述式の解答を書ききる力を身につける。

この目標をつねに念頭において、ひとりひとり、丁寧に指導しましょう。

なお解答の前半は以下のように省略してもOKです↓

次は→中学数学「連立方程式」の効果的な教え方③ 代入法

 

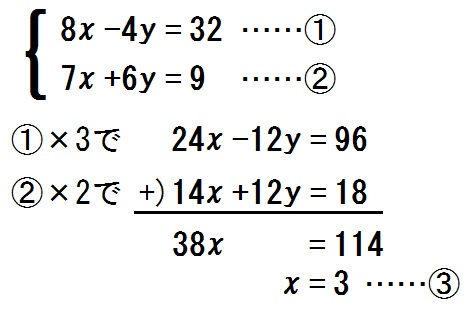
7.まとめ

以上、中２数学「連立方程式」導入～加減法の教え方でした。

２記事分の内容をまとめます。

 

次回は代入法の教え方を解説します。

指導のコツは同じですが、くわしくイメージしたいという教師・講師・保護者の方は参考にしてください。

それが終われば、小数・分数をふくむ連立方程式。

そして５回目以降に文章題を予定しています。

→中学数学「連立方程式」の効果的な教え方③ 代入法

（数学指導法の記事一覧はまとめページへ）