中1数学「平面図形」の5回目は、円とおうぎ形です。
ここではとくに、以下のような問題がわからないってなる、その原因と解決法を示します。
例3)半径 \(3\) cm、弧の長さ \(2 \pi\) cmのおうぎ形の中心角を求めよ。
例7)中心角120°、弧の長さ \(8 \pi\) cmのおうぎ形の半径を求めよ。
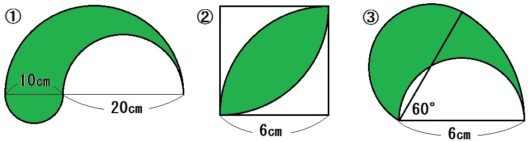
例10)下の図で、色をつけた部分の面積を求めよ。
つまり
- おうぎ形の中心角・弧・面積の求め方がわからない
- おうぎ形の半径の求め方って、どうしたらいいの?
- 円とおうぎ形の複合図形になるとチンプンカンプン
こうなる中学生へのアドバイスです。
先に結論を言っておきますね、
おうぎ形の公式は覚えなくていいから。
[中学数学「平面図形」の記事一覧]
円とおうぎ形の基本
まず、円とおうぎ形の基本を復習します。
なぜなら、おうぎ形の問題でつまずく原因は、基本をちゃんと理解していないことにあるからです。
つまずく原因
- 円周率「\(\pi\)」って「\(x\)」などと同じ文字だ、と思ってる
- おうぎ形とは何かをよく理解しないまま、ただ公式を丸暗記している
円とおうぎ形の単元でつまずく原因は、この2つです。
つまり、
- 「関数単元で習った \(x\) や \(y\) などと違って、\(\pi\) ってのはあるひとつの数字を表しているんだ」
- 「おうぎ形とは円の一部だから、そこから \(l = 2\pi r \times \frac{a}{360}\) とか \(S = \pi r^2 \times \frac{a}{360}\) とかの公式が出てくるんだな」
っていう理解が、ない。
これが円とおうぎ形問題でつまずく一番の原因なんです。
もし中学生が、
「途中式さ、両辺を \(\pi\) で割っていいの?」
「中心角を求める公式がないんだけど」
などと質問してきたら、そういう生徒はつまずいていることになります。
そこで、以下、円周率 \(\pi\) とは何か?
またおうぎ形とは何か?
きちんと理解していきましょう。
円周率 \(\pi\) とは
そもそも円周率とは直径と円周の比率のことです。
つまり
$$ \mbox{円周率} = \frac{\mbox{円周の長さ}}{\mbox{直径の長さ}}$$
で、ようするに、円周の長さって直径の何倍なの?っていう質問の答えのこと。
それが、どんな大きさの円であっても「およそ3.14」なんです。
つまり円周の長さって、かならず直径の約3.14倍なんです。
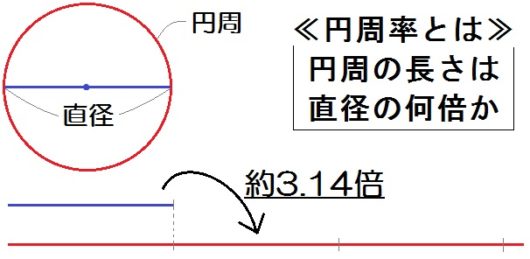
小学校まではこの円周率を「3.14」として計算してきました。
しかし、正確には3.14じゃありません。
円周率ってじつは無限につづく小数なんです。
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 ……
だから中学生になって、算数から数学になって、もっと正確な計算をしようとしたら、3.14では不十分です。
でも無限につづく小数を答案用紙に書くことはできません。一生かかってもムリ。
じゃどうするかというと、記号で置き換えようと。
それが「\(\pi\) (パイ)」。
ということで、\(\pi\) とは何かというと、3.14159265……と無限につづく小数を書ききれないから代わりに持ってきた記号。
そして円周率というひとつの数字を表している定数なのでした。
[参考記事]
比例と反比例② 関数の導入と用語の説明「変数と定数」
おうぎ形は円の一部
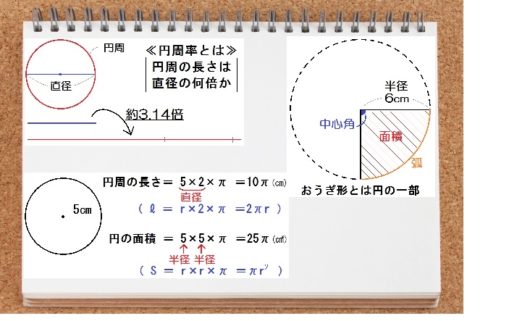
よって、小学校で習った円の公式は、以下のように言い換えられます。
円周の長さ=(直径)× \(\pi\)
( \(l=2 \pi r \) )
円の面積=(半径)×(半径)× \(\pi\)
( \(S= \pi r^2 \) )

それぞれの下に、記号による公式も書きましたが、覚える必要はありません。
ただ図をみて理解できればOKです。
さて。
ここまできたら、次におうぎ形とは何か理解しましょう。
おうぎ形とは円の一部のこと。
ようするに、ピザのひときれのことです。
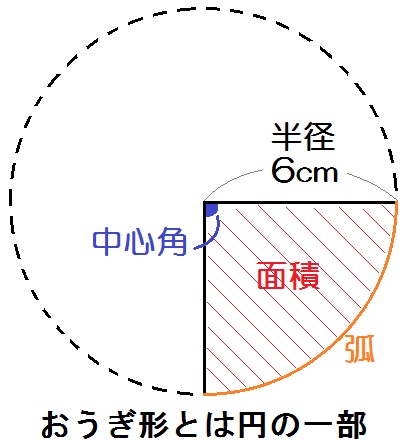
図では、円の \(\frac{1}{4}\) のおうぎ形を描いてみました。
このおうぎ形の
- 弧の長さ
- 面積
- 中心角
を求めてみましょう。
ポイントは「 \(\frac{1}{4}\) 」という割合です。
公式は覚えなくていい!
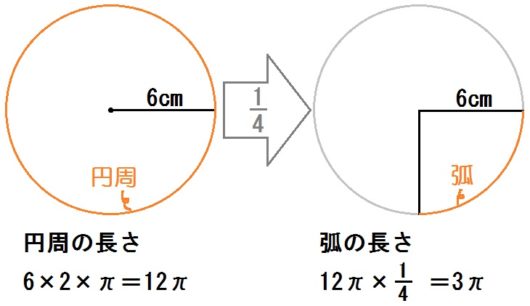
まず弧の長さ。
おうぎ形って円の一部だから、弧=円周の一部です。
だから(円周)× \(\frac{1}{4}\) をすればいい。
円周の長さは
$$ 6 \times 2 \times \pi = 12 \pi $$
よって、求める弧の長さは
$$ 12 \pi \times \frac{1}{4} = 3 \pi $$
答.\(3 \pi \) cm と出ます。
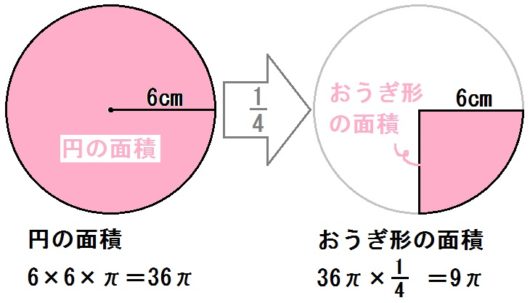
つぎに面積。
おうぎ形って円の一部だから、おうぎ形の面積=円の面積の一部です。
だから(円の面積)× \(\frac{1}{4}\) をすればいい。
円の面積は
$$ 6 \times 6 \times \pi = 36 \pi $$
よって、求めるおうぎ形の面積は
$$ 36 \pi \times \frac{1}{4} = 9 \pi $$
答.\(9 \pi \) ㎠ と出ます。
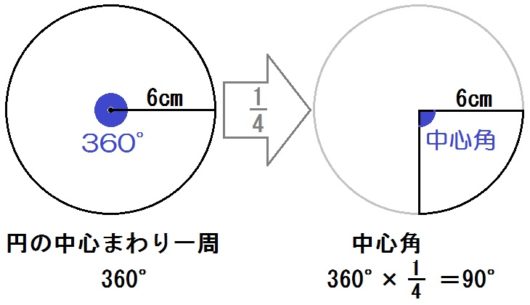
最後に中心角。
おうぎ形って円の一部だから、中心角=中心まわり(360°)の一部です。
だから(360°)× \(\frac{1}{4}\) をすればいい。
$$ 360 \times \frac{1}{4} = 90 $$
答.\(90\) ° と出ます。
このように、おうぎ形の問題はすべて、まず全体の円を求めてそれに割合をかけてやる。
そうすればどんな応用問題でも解けます。
だから公式を覚える必要はないんです。割合さえ出しちゃえば。
以下では、例題とともに、このことを見ていきましょう。
[参考記事]
・中学数学「1次方程式」文章題の解き方⑧【割合の問題】
中心角・弧・面積の求め方

おうぎ形における中心角・弧・面積という3点セット。
これらの求め方は今言ったように、
- どれか1つから \(\frac{\mbox{おうぎ形}}{\mbox{円全体}}\) という割合を出す
- 円全体を求める
- それに割合をかける
という手順です。具体的に見ていきましょー。
中心角から割合を出す
この例題1は、中心角・弧・面積のうち「中心角 \(60\) °」がわかってます。
よって割合は
$$ \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{\mbox{60°}}{\mbox{360°}} = \frac{1}{6} $$
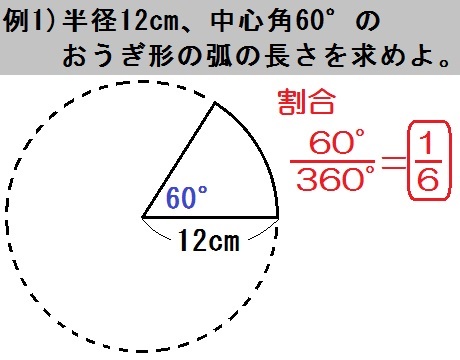
また、求めるものは「弧の長さ」なので、まず円全体の円周を出すと
$$ \mbox{(円周)} = 12 \times 2 \times \pi = 24 \pi $$
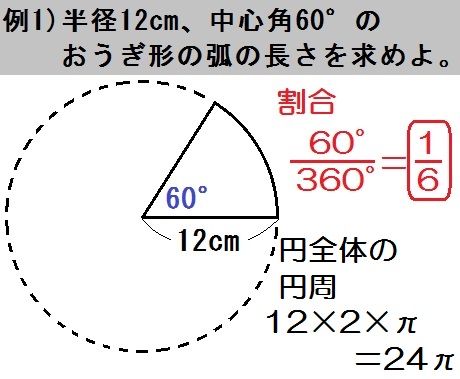
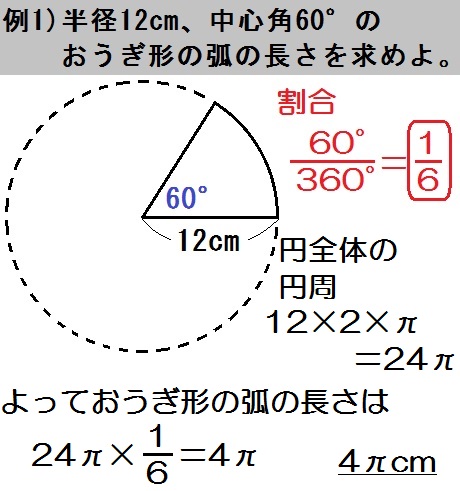
よっておうぎ形の弧の長さは
$$ 24 \pi \times \frac{1}{6} = 4 \pi $$
答.\(4 \pi\) cm と出ます。
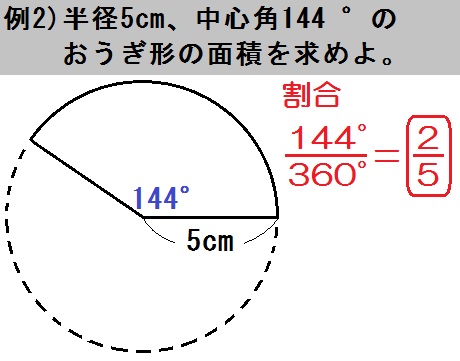
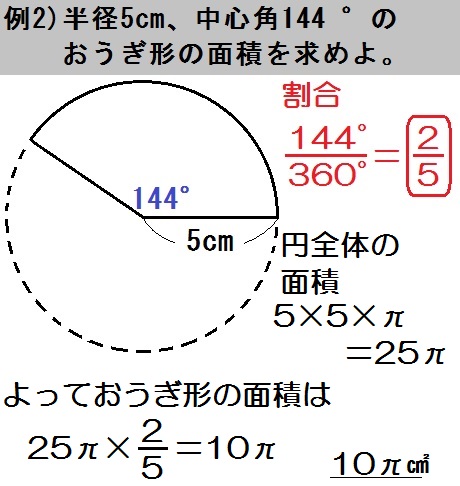
例題2も中心角・弧・面積のうち「中心角 \(144\) °」がわかってます。
よって割合は
$$ \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{\mbox{144°}}{\mbox{360°}} = \frac{2}{5} $$
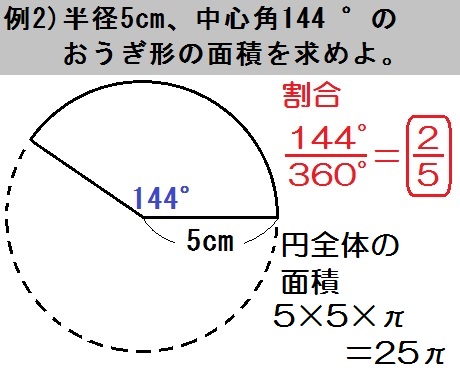
また、求めるものは「面積」なので、まず円全体の面積を出すと
$$ \mbox{(円の面積)} = 5 \times 5 \times \pi = 25 \pi $$
よっておうぎ形の面積は
$$ 25 \pi \times \frac{2}{5} = 10 \pi $$
答.\(10 \pi\) ㎠ と出ます。
弧の長さから割合を出す
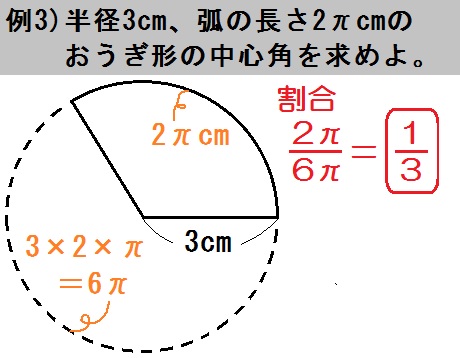
この例題3は、中心角・弧・面積のうち「弧の長さ \(2 \pi\) cm」がわかってます。
そんで半径 \(3\) cmの円全体の円周は \(3 \times 2 \times \pi = 6 \pi\) (cm)です。
よって割合は
$$ \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{2 \pi}{6 \pi} = \frac{1}{3} $$
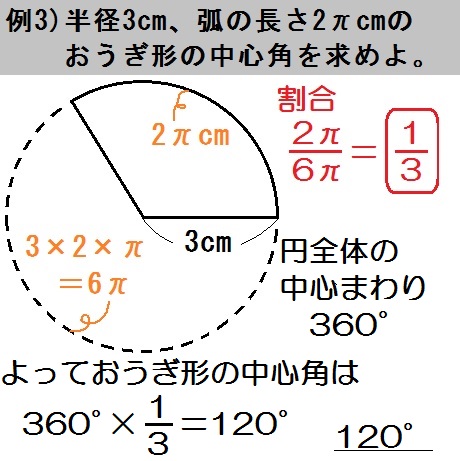
また、求めるものは「中心角」なので、まず円全体の中心まわりは \(360\) °
よっておうぎ形の中心角は
$$ 360 \times \frac{1}{3} = 120 $$
答.\(120\) ° と出ます。
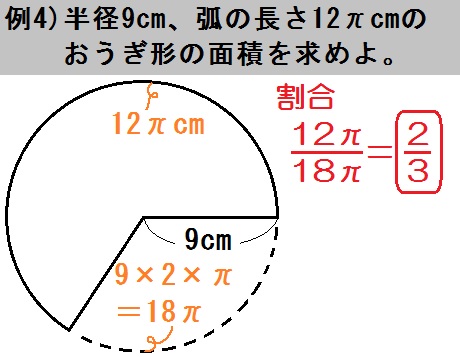
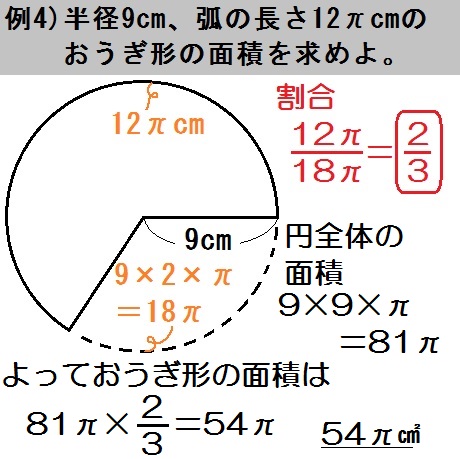
例題4も中心角・弧・面積のうち「弧の長さ \(12 \pi\) cm」がわかってます。
そんで半径 \(9\) cmの円全体の円周は \(9 \times 2 \times \pi = 18 \pi\) (cm)です。
よって割合は
$$ \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{12 \pi}{18 \pi} = \frac{2}{3} $$
また、求めるものは「面積」なので、まず円全体の面積を出すと
$$ \mbox{(円の面積)} = 9 \times 9 \times \pi = 81 \pi $$
よっておうぎ形の面積は
$$ 81 \pi \times \frac{2}{3} = 54 \pi $$
答.\(54 \pi\) ㎠ と出ます。
面積から割合を出す
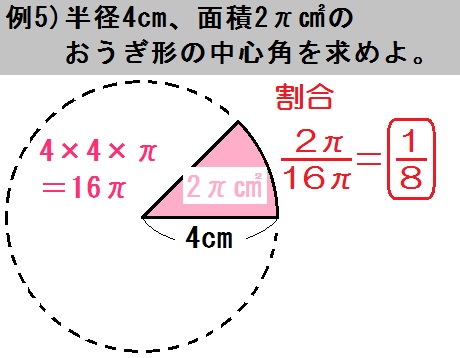
この例題5は、中心角・弧・面積のうち「面積 \(2 \pi\) ㎠」がわかってます。
そんで半径 \(4\) cmの円全体の面積は \(4 \times 4 \times \pi =16 \pi\) (㎠)です。
よって割合は
$$ \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{2 \pi}{16 \pi} = \frac{1}{8} $$
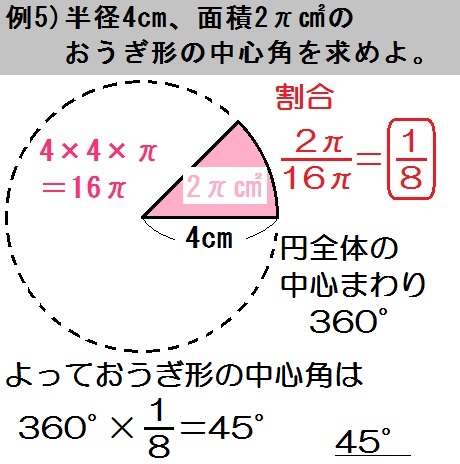
また、求めるものは「中心角」なので、まず円全体の中心まわりは \(360\) °
よっておうぎ形の中心角は
$$ 360 \times \frac{1}{8} = 45 $$
答.\(45\) ° と出ます。
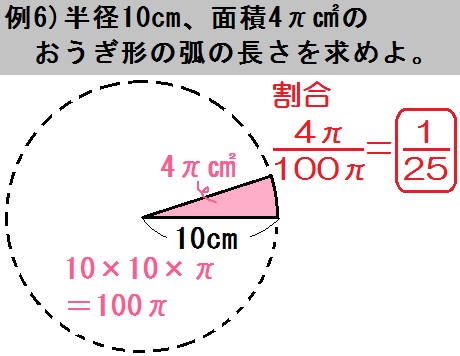
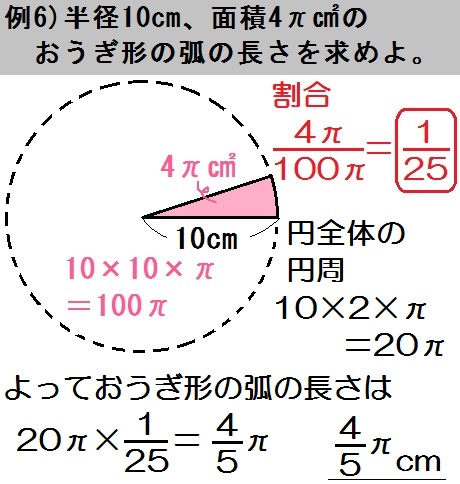
例題4も中心角・弧・面積のうち「面積 \(4 \pi\) ㎠」がわかってます。
そんで半径 \(10\) cmの円全体の面積は \(10 \times 10 \times \pi =100 \pi\) (㎠)です。
よって割合は
$$ \frac{\mbox{おうぎ形}}{\mbox{円全体}} = \frac{4 \pi}{100 \pi} = \frac{1}{25} $$
また、求めるものは「弧の長さ」なので、まず円全体の円周を出すと
$$ \mbox{(円周)} = 10 \times 2 \times \pi = 20 \pi $$
よっておうぎ形の弧の長さは
$$ 20 \pi \times \frac{1}{25} = \frac{4}{5} \pi $$
答.\(\frac{4}{5} \pi\) cm と出ます。
[関連記事]
空間図形④ 表面積の問題のコツ
練習問題
以上のように、おうぎ形の問題では、
- 中心角・弧・面積のうち、わかっている1つから \(\frac{\mbox{おうぎ形}}{\mbox{円全体}}\) という割合を出す
- 円全体を求める
・「中心角を求めよ」なら、まず円全体の中心まわり(=360°)
・「弧の長さを求めよ」なら、まず円全体の円周
・「面積を求めよ」なら、まず円全体の面積 - (円全体)×(割合)をする
これが中心角の求め方・弧の長さの求め方・面積の求め方のすべてです。
公式を覚える必要ないでしょ。
そして公式を丸暗記するより、ちゃんと理解してるから、応用範囲が広いっしょ。
では以下、練習問題を解いて、「わかる」を「できる」に変えていってください。
解答は末尾に記載、質問はコメント欄からどうぞ。
問1)次のようなおうぎ形の弧の長さと面積を求めよ。
- 半径6cm、中心角30°
- 半径5cm、中心角72°
- 半径4cm、中心角315°
問2)半径8cm、弧の長さ \(6 \pi\) cmのおうぎ形の中心角を求めよ。
問3)半径10cm、弧の長さ \(5 \pi\) cmのおうぎ形の面積を求めよ。
問4)半径12cm、面積 \(12 \pi\) ㎠のおうぎ形の中心角を求めよ。
問5)半径6cm、面積 \(27 \pi\) ㎠のおうぎ形の弧の長さを求めよ。
1-1:弧の長さ \(\pi\) cm、面積 \(3 \pi\) ㎠
1-2:弧の長さ \(2 \pi\) cm、面積 \(5 \pi\) ㎠
1-3:弧の長さ \(7 \pi\) cm、面積 \(14 \pi\) ㎠
2:135° 3:\(25 \pi\) ㎠ 4:30° 5:\(9 \pi\) cm
次は応用問題として
- おうぎ形の半径の求め方
- 円とおうぎ形の複合図形
を解説します。
[中学数学「平面図形」の記事一覧]




コメント
問9の3の周りの長さの解説お願いします。
直径24cmの円周ひとつぶん+直径12cmの円周ひとつぶん
式をつなげて書く、というのは、地味に大事だと思います。
理由としては、上に挙げられている、計算が楽、のほか、
個々に計算した後、足したり引いたりすると、
足すのを忘れたり、引くのを忘れたり、ということが往々にしてあるので、
最初につなげて書くことで、それを防げる、ということも言えるかと思います。