数学の証明とは何か?
いつ・誰が・どのように考え出したのか?
どうしてこんなにめんどくさいのか?
なぜ私たちは数学の証明を勉強させられるのか?
これ、ジュウゴにはずっと疑問でした。
絶対値のように「はあっ!?」と叫ぶことはなかったんですが、教育に携わってきたので、嫌でも生徒のこうした疑問に向き合わなければなりませんでした。
証明単元になるたび、子どもは言います。
「できない・難しい・わからない・めんどくさい」と。

このうち「できない・難しい」は指導技術の向上で解決しました。
でも「(そもそもなんでこんなことするのか)わからない」、「(ここまで厳密にやることが正直)めんどくさい」という後者2つの声には、十分に答えられなかったのです。
そこでこのコラムでは、いろいろ調べた結果ジュウゴが得た知識をもとに、数学の証明がもつ意味・意義を解説していきます。
学力に余裕のある中3生や高校生、また講師や家庭教師、保護者の方向けの、ちょっと深い話になります。
(証明の指導方法については中学数学の指導の連載で解説する予定です)
数学の証明とは何か?

まず数学における証明とは何か、確認しましょう。
数学でいう「証明」とは一般的な「説明」とはちがいますし、「科学的証明」ともちがいます。
何がどうちがって数学の証明になるんでしょう?
「演繹」と「一般化」
数学の証明とは、以下2点の特徴をもつものをいいます。
- 数ある推論方法のなかでも「演繹」だけを使う
- すべての場合に当てはまるように「一般化」をしなければいけない
1.から説明します。
人間が未知の事柄を予想する手段というのはいろいろあります。
- 経験(ひとりの女にだまされた→女には気をつけねばならない)。
- 類推(チンパンジーは共同で狩りをする→初期人類もそうだったにちがいない)。
- 仮説形成(会社の売り上げが悪い→接客が原因だと仮説を立てる)。
- 帰納的推論(ある遺伝子異常をもつ100人がみな同じ病気だった→この遺伝子異常が病気の原因である)
- 演繹的推論(人間はみんな死ぬと仮定する→ジュウゴは人間である→よってジュウゴは死ぬ)
わたしたちは日頃、これらの予想手段を区別することなく使っています。
しかし数学の証明においては、演繹的推論以外は「不確実な手段だ」として切り捨てるのです。
類推による証明
演繹以外の手段がどうして不確実なのか、実際に証明方法を比べることで見てみましょう。
たとえば「三角形の内角の和は180°である」という事柄を、「類推」「帰納的推論」「演繹的推論」の3通りで証明してみます。
≪類推による証明≫
問題)三角形の内角の和は180°であることを証明せよ。
証明)図のように、正三角形を書いて角度を測ったらすべて60°だった。
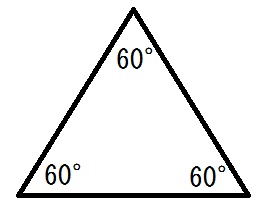
\(60+60+60=180\) なので、正三角形の内角の和は180°である。
三角形はみな、正三角形と似たようなものである。
よって、三角形の内角の和は180°である。
この証明に納得できますか?できませんね。「三角形はみな正三角形と似たようなものである。よって……」の部分が、つっこみどころ満載ですもんね。
だから類推による証明は、いくらでも反論可能ということです。
科学的証明(帰納)
次に、帰納的推論で証明してみましょう。
この帰納的推論をつかった証明がいわゆる科学的証明というやつです。
≪科学的証明≫
問題)三角形の内角の和は180°であることを証明せよ。
証明)三角形をランダムに1万個作って角度を測ったら、その内角の和はすべて180°だった。
証拠は十分である。
よって、三角形の内角の和は180°である。
この証明はどうでしょう?たいていの人は納得するかもしれません。
しかし疑り深い人が「1万1回目は180°じゃないかもしれない」と言い出すかもしれません。
じゃあ10万回試したところで、10万1回目は?となってしまいます。
このように、科学的証明というのは「絶対にそうだ」とは言えない証明なんです。
「見たかぎり、試したかぎりではそうだった」としか言えないんです。
これが帰納という推論方法の限界です。
[関連記事]
科学の歴史の流れを超簡単にまとめてみた① 18~20世紀
数学的証明(演繹)
最後に演繹的推論による証明、つまり数学的証明を見てみましょう。
≪数学的証明≫
問題)三角形の内角の和は180°であることを証明せよ。
証明)図のように平行線を引き、またそれぞれの角度を \(a\) , \(b\) , \(c\) とする。
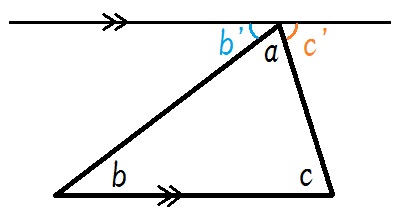
平行線公理を認めれば、平行線の錯角は等しいので、
$$ b=b’ \ , \ c=c’ \quad \mbox{…①} $$
また一直線は180°なので、
$$ a+b’+c’=180 \quad \mbox{…②} $$
①②より
$$ a+b+c=180 $$
よって、三角形の内角の和は180°である。
いかがですか?
この証明だけが、なぜ三角形の内角の和は180度になるのかを説明していますね。
つまり演繹という方法は「なぜそうなるのか」という理由を既知の事柄にさかのぼってちゃんと説明できるんです。
だから数学の証明では、演繹だけを使うのです。
そして、この数学的証明だけが、「どんな角度であっても必ずそうだ」といえる内容にもなっています。
類推も、科学的証明も、まだ試していない三角形が無限にあるので、「必ずそうだ」とは断言できません。
これはなぜかというと、文字を使って角度を一般化していないからです(文字による一般化については後半で詳述します)。
どんな場合にも当てはまるように、一般化すること。
これが数学の証明だけがもつ、もうひとつの特徴なのです。
数学の証明とは
- 数ある推論方法のなかでも「演繹」だけを使う証明のこと
- すべての場合に当てはまるように「一般化」をしなければいけない
[関連記事]
中2数学「式による説明」のコツと練習問題
いつ・誰が・どのように考え出したのか?

では、なぜ数学の証明はこんな特徴をもつようになったのか?
いつ・誰が・どんな目的で「推論には演繹だけを使わなきゃいけない」「一般化して証明しなきゃいけない」としたのか?
結論をいえば、紀元前6~3世紀の古代ギリシア人たちが「絶対確実な真理」を求めたためでした。
数学から道具の役割を奪ったギリシア人
古代ギリシア人というのは歴史上でみてもかなり変な人たちです。
それまで数学というのは帳簿をつけるための道具、田畑の面積を測るための道具、ピラミッドを建てるための道具として使われてきました。
なのに、ギリシア人はその数学から道具という役割を取り除きました。
そして具体例から離れて、数それ自体を研究していくのです。
つまり「家族3人」「畑3㎡」「高さ3フィート」などという具体から「3」という概念を切り出して、抽象的に扱いはじめたのです。
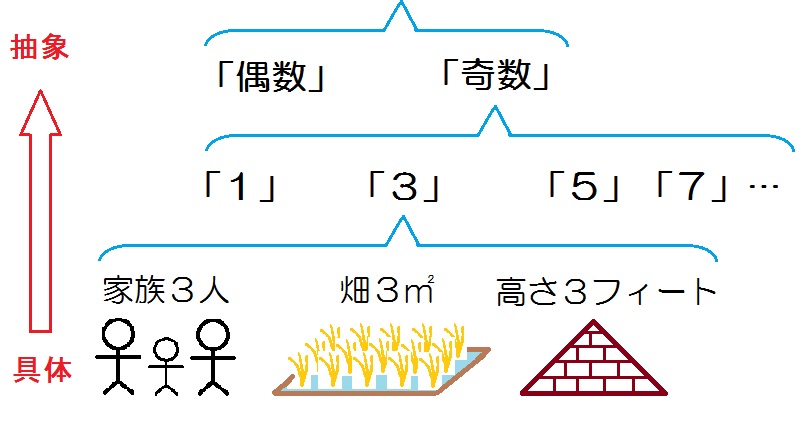
なぜギリシア人は数学を道具として使うことをせず、数学それ自体に価値を見出したのか?
かれらは具体よりも抽象が、現実よりも理想が、経験よりも論理が、そして変化よりも永遠が大好きだったからです。
これはかれらの社会形態と関係しています。
奴隷がいたから演繹のみとなった
古代ギリシア社会の市民たちは多くの奴隷を保有していました。
上層市民であるほど奴隷の数は多く、家事や育児、商売や医療まで、およそ生きるためのほとんどすべての活動を奴隷任せにすることができました。
この結果、上層市民である学者や芸術家は、雑事を、手作業を、生活を、現実を嫌い、日々思索に没頭するようになったんです。
ピタゴラスもプラトンもアリストテレスもアルキメデスも、商売なんかする奴は卑しい、道具としての数学など価値がない、純粋な知識のみが最高であると放言しています。
こういう日々を送る哲学者・数学者にとって、経験などは予想手段として論外です。
また日々の経験がないから、仮説形成という推論方法も重要とは思えません。
そして手作業を嫌うから、何回も実験する帰納的推論など、もってのほかです。
こうして古代ギリシア人にとって確実な推論方法は「演繹のみ」となったのでした。
抽象の世界で真理を求めたから一般化
また、生きることにあくせくせず、思索にふける毎日を送ると、人はこの世の無常を感じるようになります。
家族もいつか死んでしまう、田畑もやがて無くなってしまう、堅牢な建造物も永遠ではない……。何かひとつでも、絶対確実な永遠不変の真理というものはないだろうか……。
こうした思いから、古代ギリシアの学者たちは先述したように、具体よりも抽象の世界にのめりこんでいったのでした。
抽象的に考えることは、具体的に考えるより難しい思考です。
一般的な三角形について論じるより、具体的なあるひとつの三角形を考えたほうがイメージしやすいのは、数学の証明問題に悩まされてきたすべての人が感じるところでしょう。
でも古代ギリシア人たちは、やっぱり抽象的に考えるほうを選んだ。なぜなら絶対確実な永遠不変の真理は、このうつろいやすい現実世界にはなく、抽象的に考えた理想の世界にしかないからです。
こうして数学の証明もまた、抽象的に、つまり一般化して考えるものとなりました。
- 点とは大きさのない位置である
- 線とは幅のない長さである
- 面とは長さと幅のみをもつものである……
具体的イメージをもたない、極度に抽象化・一般化された定義や、証明のしかた。
古代ギリシア人たちの一風変わった性向によって、これが出来上がったのでした。
数学の証明はなぜ「演繹」と「一般化」という特徴をもつのか
- 数学から道具としての役割を取りのぞいてひとつの学問に仕立てた古代ギリシア人が
- 奴隷をいっぱい持っていたため現実を軽視し、経験や帰納などの推論を嫌ったから
- また抽象の世界で絶対確実な永遠不変の真理を求めたから
[関連記事]
世界三大宗教の本質を簡単にまとめてみた1 キリスト教とイスラーム教
どうしてこんなにめんどくさいのか?

このようにして、数学で何かを証明するときには、「あらゆる場合に当てはまる」と一般化して述べないといけなくなりました。
では、数や長さや角度など、具体的な値をどうやったら一般化できるのか。
文字を使えばいいんです。
そしてこの文字の使用が、数学の証明をあれほどめんどくさくしている原因でもあります。
文字を使って無限をカバーするから
中2「式による説明」のコツでもちょっと書きましたが、証明で文字を使うメリットは、無限をカバーできる点にあります。
たとえば以下の問題↓
問題)偶数と奇数の和は奇数になる。このわけを証明せよ。
証明)\(m\) , \(n\) を整数とすると、
偶数は \(2m\) 、奇数は \(2n+1\) と表せる。
\begin{eqnarray} & & 2m+(2n+1) \\ &=& 2m+2n+1 \\ &=& 2(m+n)+1 \end{eqnarray}
\(m+n\) は整数なので、\(2(m+n)+1\) は奇数である。
よって、偶数と奇数の和は奇数になる。
なぜ、こんなにめんどくさく書くのか?
\(m\) と \(n\) という文字を使えば、\(m\) と \(n\) にはどんな整数を入れてもいいので、あらゆる偶数・あらゆる奇数がぜんぶカバーできるからです。
逆にいえば、あらゆる偶数・あらゆる奇数をぜんぶカバーするために、わざわざ偶数と奇数を\(m\) 、\(n\) という文字を使って表すんです。
「\(2+3=5\) 、ほら、成り立つよ」なんて言っても、これじゃひとつの例しか試してないですもんね。
なんで証明方法は今でも変わらないの?
文字を使って一般化して証明する。
これは古代ギリシア人の特殊な性格から来ている。
ここまではOKだと思います。
しかし、なんで現代のわたしたちまでそんなめんどくさい方法に従わなければいけないのか?勝手にやってろよ!
こんな疑問(というか不満)も出てきます。
この疑問にたいする回答は3つです。
- いちど一般化して証明すれば、あらゆる現実に対応可能だから。
- そんな便利さのため、17世紀以降、数学が近代科学の土台となったから。
- そして21世紀の現代社会も、近代科学文明の延長にあるから。
最後に、この3点を見ていきましょう。
[関連記事]
科学の歴史の流れを超簡単にまとめてみた① 18~20世紀
なぜ私たちは数学の証明を勉強するのか?

図形の証明をはじめ、中学・高校数学でわたしたちは嫌というほど証明を勉強します。
これには、紀元前から連綿とつづく人類の知識の歴史に、その理由がありました。
エウクレイデス(ユークリッド)の『原論』
紀元前300年頃、古代ギリシア人であるエウクレイデス(ユークリッド)が『原論』という本を書き、数学の証明というスタイルを完成させます。
エウクレイデスはわずかな定義と公理から出発して、400以上の定理を証明しました。
そこには「三平方の定理」のように先人たちの業績も多くありましたが、それらをまとめて体系化したのがエウクレイデスだったのです。

エウクレイデス
(Wikipediaより)
演繹と一般化によって証明された事柄は、定義と公理を認めるかぎり、疑いようがありません。
だから例えば、
$$ \mbox{(円錐・角錐の体積)} = \mbox{(底面積)} \times \mbox{(高さ)} \times \frac{1}{3}$$
のような『原論』中の定理は、安心して、あらゆる円錐・角錐に使えます。
[関連記事]
中学数学「平面図形」③ 体積の問題のコツ
この確実さ、応用の広さ、ついでに美しいほど論理的な記述によって、『ユークリッド原論』は時代をこえて読み継がれました。
ヨーロッパでは中世の大学で教科書となり、イスラーム世界では『原論』をもとにさらに数学が発展しました。
こうして、古代ギリシア風の証明スタイルは、難しいけれど確実で、しかもいろんな現実に応用可能なすげー知識として、1000年以上受け継がれていったのです。
科学を支える数学、数学を支える証明
1096~1270年の十字軍によって、中世ヨーロッパはイスラーム世界の発展した知識に触れます。
そこからルネサンス、宗教改革を経て、17世紀には近代科学が本格的に誕生してきました。
近代科学とは簡単にいうと、それまでの世界観をいったん捨てて、新たな枠組みで世界をとらえなおそうという試みでした。
では、それまでの目的論的世界観や信仰に代わる、新たな枠組みの土台は何にすべきか?
デカルト、ガリレイ、ニュートンたちが選んだのが、数学だったのです。
(近代科学とは何か、近代科学において数学はどんな役割なのか、詳しくは以下の連載で解説しています↓)
こうして数学が近代科学の土台となりました。
世界を数量的にとらえる近代科学と数学の相性はバッチリで、これ以降、科学の発展に数学はなくてはならないものとなります。
同時に、科学が確実な知識であるためには、土台である数学もまた確実性を求められました。
こうして17世紀以降、数学の証明の重要性がふたたびクローズアップされたのです。
そして日本の教育でも
ヨーロッパの近代科学文明はその後、19・20世紀にかけて、世界中を覆い尽くします。
すでに産業革命を経たヨーロッパの科学が、黒船や大砲となって出現すると、日本もたまらず開国、積極的に科学文明を取り入れていきます。
(ヨーロッパが世界を覆う過程は、以下の記事で詳しく解説しています↓)
こうして明治以降、日本の公教育に、数学の証明が入りました。
科学の土台は数学であり、数学の土台は証明であるということで、富国強兵をめざす日本においては数学の証明も必須の知識となったのです。
ちなみにそれまでの日本は和算が主流でしたが、そろばんの伝統以外はすべてすたれていきました。
たとえば明治40年(1907年)の入試には、こんな証明問題があります(時間のある方はどうぞ)。
ある円上の点Pにおける接線と、他の2つの平行な接線との交点をそれぞれA,Bとするとき、この円の半径はAP-PB間の比例中項となる。このことを証明せよ。
東京高等商業高校 明治40年 博究社HPより
こうした流れが、21世紀の現代にまで続いている。
わたしたちが学校で数学の証明を習うのは、以上のような理由だったのです。
[関連記事]
ヨーロッパの歴史の流れを超簡単にまとめてみた
まとめ

○数学の証明とは何か?
- 数ある推論方法のなかでも「演繹」だけを使う証明のこと
- すべての場合に当てはまるように「一般化」をしなければいけない
○いつ・誰が・どのように考え出したのか?
- 数学から道具としての役割を取りのぞいてひとつの学問に仕立てた古代ギリシア人が
- 奴隷をいっぱい持っていたため現実を軽視した
- また抽象の世界で絶対確実な真理を求めた
- それで「演繹」と「一般化」という特徴をもつ証明が生まれた
○どうしてこんなにめんどくさいのか?
- 文字を使って無限をカバーするから
○なぜ私たちは数学の証明を勉強するのか?
- 数学の証明は確実で、広く応用できるから、エウクレイデスの『原論』を通じて受け継がれた
- 17世紀には数学が近代科学の土台となったため、証明にふたたびスポットライトが当たった
- この近代科学文明が世界中を覆い、いまでもそうだから、21世紀の日本でも数学の証明が学ばれる
以上、数学の証明にはどんな意味があるのかのコラムでした。
最後にふたつほど。
ひとつ。「証明ができない、難しい、わからない、めんどくさい」という中高生に、このコラムの内容を話してもムダです。
かれらに必要なのは証明する意味を伝えることじゃなくて、なんのためかよくわからんけどとにかく問題が解けるようになることですからね。
正負の数② 乗除・累乗の記事でも書きましたが、証明問題が解けない生徒には、まずびしっと解き方を習熟させる。ここの話を語るのはそれからにしてください。
習熟のさせ方については中2「平行と合同」単元にいずれアップする予定です。
ふたつ。数学の証明ができると何かいいことがあるの?
こういう「お皿洗いしたから服買って」的な質問にも、いちおうの答えを考えてみました。
ジュウゴの回答は、ひとつ挙げるなら、
- 逆説的に人間の多様性を知るきっかけになる
というものです。
世界には、物を盗んだだけで腕を切られたり、奴隷を所有していたり、クジラを食べたりと、じつにさまざまな考え方・習慣があります。
そういう多様性に富んだ人類が、唯一「たしかにそうだ」と全員納得できるのが、数学の証明なんです。
だから逆にいえば、あれだけ厳密化しないと人間みなが納得できるものとはならない。他人に何かをわかってもらう・他人と共通の理解に達するということは簡単なようでじつはとっても大変なことなんだ。
そんな意識の萌芽に、数学の証明は役立つと思います。
特に「おれが正しいと思うことはみんな正しいと思うはず」「わたしの気持ち、わかって当たり前でしょ」って人ほど、共通理解の難しさに触れるという点で、効果的ではないでしょうか。
人格が固定する前の中高生段階で数学の証明を学ぶ意義は、ここにもあるように感じます。












コメント
とても素晴らしい記事です!ありがとうございます! ただ、数式部分が [Math Processing Error] となって表示されていませんでした。