近代科学の特徴その2。いろんな副産物と、数学のはたした役割

こんにちは、重悟（ジュウゴ）です。
前回につづいて、近代科学の特徴を解説していきます。

前回は近代科学の特徴が「現象の量れるところだけ量って、問題を数学におきかえる」ってところにあることを解説しました。

今回はこうした特徴によって、近代科学が他にもいろんな特徴をもつようになったこと、そして数学の果たす役割がおおきくなったことを見ていきます。

このページを最初に開いた方は、まず前回の記事から読んでみてください。

近代科学の副産物その1：あたらしい量の概念

近代科学は量に注目するんでしたね。

石が落ちるという現象を説明しようとするとき、なぜ石が落ちるとか、石の質感とか、石の存在理由とかは置いといて、石の重さや、落ちる時間や距離や速さといった「量で表せるもの」だけに注目してとにかく量る。

これが近代科学の特徴でした。

 

新しい「量」が生み出される

こうした態度がすすむと、「もっとほかに量れるものはないか」と探す人が出てくるのも当然です。

それで長さとか、温度とか、体積、密度、圧力なんてものまで量るようになります。

 

この態度がさらにすすむと、「あたらしい量もつくっちゃおう」という動きが出てきます。

それで17世紀以降、新しい量の概念がつぎつぎと生み出されていきました。

つまり、質量、力、加速度、運動量といった概念のことです。

これらの概念はただ便利という理由で生み出されたのですが、おかげで物理を学ぶ生徒はいまでも苦労するわけです。

質量、加速度、力とは何か

ひとつひとつの量についてくわしく説明はしませんが、質量や力といった言葉はいまではふつうに使われるようになりました。

ただ厳密に「質量とは何か」を話し出すと、とてもむずかしい話になってしまいます。

かんたんにいえば、質量とは物質固有の動かしにくさを量で表したもので、重さとはちがいます。

 

また加速度とは速度の変化の割合のことで、前回の記事で紹介した「16」に当たります。

そして力とは質量×加速度を計算したもので、式にすると

F=ma（Fが力、mが質量、aが加速度）
となります。

これを定義したのがニュートンです。

あの『自然哲学の数学的原理』という本のなかで言い出しました。

いまでは物理の基本法則になっていて、理工系の学生にとってはなじみ深い式でもあります。

「おいおい、こっちは文系出身なんだ。急に数式とか出すんじゃねえ」という方。

すいません。わたしも文学部出身です。

背伸びしちゃいました、ごめんなさい。

でもじつは、こうした数式が科学で使われるようになったというのが、近代科学の2つめの副産物でもあるのです。

 

近代科学の副産物その2：量の関係を表す関数式

現象のいろんな量をはかるようになると、つぎに考えるのは、量と量のあいだになにか関係はないだろうかということです。

つまり石の落ちる「時間」と「距離」とのあいだには、なにか関係はないものか、いやきっとあるはずだと、ガリレイやそれ以降の学者たちは考えるようになりました。

 

量どうしの関係を表す「関数」

そこで学者たちが使ったのが、関数という数学の分野です。

関数とは2つの量の関係を表した式やグラフのことです。

中学で習った比例・反比例とか2次関数とかの、あれです。

ちなみに関数という分野を整備したのはガリレイと同時代人であるルネ・デカルト。

あの「われ思う、ゆえにわれ在り」とつぶやいたおっさんですね。

この関数というあたらしい数学分野をつかって、学者たちは量どうしの関係を式で表していきました。

たとえば、前回のガリレイの実験で、石の落ちる「時間」と「距離」との関係はつぎの式で表せます。

d=16t²（dは石の落ちた距離、tは石の落ちた時間）

この式で、時間と距離との関係をすべて表したことになります。

たとえば1秒後の石の落ちた距離は16×1²で16m、2秒後の距離は16×2²で64m、3秒後の距離は16×3²で144m、4秒後の距離は16×4²で256mと、はかった距離とすべてぴったり合っています。

関数の利用が数学と科学をむすびつけた

こうして「石が落ちる」という現象を、たったひとつの式で表せるようになりました。

このことが当時の人たちにとっては衝撃でした。

「ひょっとして、この世界のあらゆる現象はすべて数式で表せるんじゃないか？」

こうして学者たちはいろんな現象の量をはかって、そして量の関係を関数の式で表そうとしはじめるのです。

この特徴が現代にまでずっとつづいているんですね。

たとえばアインシュタインが特殊相対性理論の付録として発表した「E=mc²」という式も、エネルギーと質量という2つの量の関係を表したものです。

 

量の関係を関数で表すことができる。

この発見によって、科学のなかで数学のはたす役割は大きくなりました。

それまでは自然の研究と数学とはまったく別の学問でしたが、17世紀以降、2つの学問は相思相愛、離れられない仲になるわけです。

ちなみに関数という数学分野も発展を遂げて、微積分から解析へとすすんでいきますが、このあたりの話はまたいつか数学コラムのほうでまとめる予定です。

 

「現象を関数で表すようになったのはわかった。でもそれってただ学者たちの自己満足なんじゃないの。なんかいいことでもあんの？」と思ったあなた、するどい指摘です。

じつはとってもいいことがあります。未知の内容を予測できちゃうんです。

＞Amazonプライム・ビデオ「未知との遭遇 ファイナル・カット版」

 

近代科学の副産物その3：わからないことが予測できちゃう

未来の出来事が予測できちゃう

たとえばガリレイの「石が落ちる」という現象を表した以下の式。

d=16t²（dは石の落ちた距離、tは石の落ちた時間）

これを使えば、10秒後に石がどこにいるかを予測することができます。

tに10を入れて計算すればいいんですから（塔がめっちゃ高ければという条件付きですが）。

これは「10秒後という未来の出来事を、数学をつかって予測できちゃう」例です。

万有引力の公式で予測できちゃう

また、もっとすごい威力をもった式を紹介しましょう。

ニュートンの発表した「万有引力の公式」というやつです。

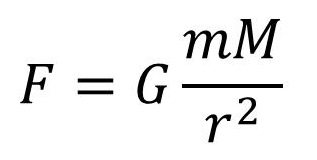
（Fは力つまり万有引力、rは2つの物体間の距離、mとMは2つの物体のそれぞれの質量です。またGは決まった数ですがとっても小さい数なので、「引力（gravitation）」の頭文字で表しています。）

この式もまたニュートンが『自然哲学の数学的諸原理』という本のなかで、「おそらくどんな物体のあいだにも、この万有引力の式が成り立つよ」と発表したものです。

そしてニュートンやそれにつづく学者たちはこの式を使って、いろんなことを予測しちゃいました。

 

たとえば地球の質量

Fは地上の物体にはたらく力を計れば出てくるので、リンゴでもなんでもいいから落っことして計ります。

rはこの場合、地球の半径だから、すでに古代ギリシア人が測っています。（地球の半径の測り方はこちら）

mにはリンゴの質量を入れます。

するとわかっていないのはM、つまり地球の質量だけ。

こうして計算すると、地球の質量がだいたい6000000000000000000000トンと予測できちゃうわけです。

地球と月のあいだの引力

rに地球と月との距離を、mに月の質量を、Mにさっきの地球の質量を入れて計算すれば、Fが出てきます。

こうして地球と月とのあいだにはたらく引力がわかって、ついでに潮の満ち引きなんかも説明できちゃうわけです。

 

彗星の軌道

ニュートンと同時代人のエドモンド・ハレーという人は、万有引力の公式とニュートンの考え方をつかって、彗星がつぎにいつ地球に近づくかを予測して、みごと的中しました。

こうして当てられた彗星には「ハレー彗星」という名前がつけられたわけです。

 

ほかにも予測できることはたくさん

ほかにも、数式によって予測できることは数限りなくあります。

「E=mc²」という式からは原子爆弾の威力が予測されて、じっさいに使われちゃったわけですし。

わからないことが数式によって予測できるようになったことで、近代科学はその威力がみんなに認められていくのです。

 

ただ、数式がまちがっていたら元も子もありません。

「ごめん、d=16t² じゃなくて d=15t² だった、てへ」なんてまちがいをしていたら、10秒後の石の位置がぜんぜんちがってくるわけですから。

つまり、予測のもととなる数式はじっさいの現象とぴったり合っていなきゃいけないんですね。

そこで、ガリレイやいろんな学者の考えた数式が本当に合っているかどうか、確かめる必要が出てきます。

この確かめる方法というのが、実験です。

 

近代科学の副産物ラスト：実験がさかんになる

科学の実験はみなさんも学校でさんざんやらされたやったのでおなじみですね。

薬品をまぜて出てきた物質を量ったり、台車を斜面でころがして時間ごとの移動距離を測ったりといったものです。

ちなみに顕微鏡で細胞をのぞいたりアサガオを育てたりというのは、実験ではなくて「観察」です。

こんな実験がひろくおこなわれるようになるのが、17世紀の近代科学誕生からなんです。

 

実験をするのは数式（仮説や理論）を確かめるため

なぜ実験をするかというと、さきほども述べたように、その数式（より一般的にいえば仮説や理論）が本当に正しいかどうか確かめるためです。

ガリレイのやったのと同じ方法で、石を落して時間と距離を測り、本当に d=16t² という数式に当てはまるかどうかを確認するのです。

もし当てはまるなら、その数式は正しいことになります。

もし当てはまらないなら、その数式がまちがっているか、あるいは実験のどこかに不備があるといえます。この場合は条件をいろいろたしかめて何度も再実験をします。

 

このようにして、数式はその正しさを検証することができます。

実験をすることでだれでもその理論の正しさを確認できる。

これもまた、近代科学とそれ以前の科学とのちがいなんです。

近代科学以降、実験がさかんになった

たとえばアリストテレスの理論の正しさを確かめようとしても、だれもできません。

「土は地球の中心を本来の居場所とする。だから土のかたまりである石は地球の中心にむかって運動するのだ」と言われても、「へー、そー」としか言いようがないです。

でもガリレイが「1秒後に石は16m落ちる。2秒後には64m、3秒後には144mだ。だから時間をt、落ちる距離をdとすると d=16t² という数式が成り立つ」と言ったら、確かめることができます。「ホンマかいな、いっちょやったろか」と、追従実験をすることができます。

これができるのも、近代科学が「現象の量だけはかる」という本質をもっているからです。

時間や距離や速さや重さだったら、だれでもあとからかんたんに確かめられますもんね。

 

というわけで、17世紀以降の科学は実験がさかんにおこなわれるようになりました。

加速器なんて何百億円もする実験設備を作っちゃうのも、もとをたどれば近代科学のこうした特徴に端をはっするわけです。

 

 

まとめ

以上、近代科学の副産物を4つみてきました。
ここまでの内容をまとめます。

• 近代科学の特徴は「現象について量れるところだけを量ること」
• いろんな量がもてはやされて、あたらしい量もたくさん生まれた
• 量どうしの関係を表すために、数学、とくに関数が使われはじめた
• 関数をつかえばいろんな予測が可能になった
• 実験によって理論の正しさを確かめることもできるようになった

これらの特徴をもっていたおかげで、近代科学はやがて一大学問分野へと発展していくわけです。

そして19世紀以降には技術とむすびついて「科学技術」となり、人間の生活を劇的に変えていくんです。

 

次回は近代科学にまつわるたくさんの誤解について、書いていく予定です。

NEXT→近代科学の特徴その3。近代科学について書かれたものには誤解がいっぱい！