中学数学「比例と反比例」の教え方④　反比例の式を求める

中１数学「比例と反比例」の教え方４回目。

今回は反比例の式を求める問題の指導方法です。

前回と流れは同じなので、前置きは無しにして、いきましょう。

反比例の式を求める

 

指導案（前半）

１．前回までに、\(y= \mbox{(xを使った式)}\) が関数の式、

その中でも、\(y=ax\) の形を比例という、と習った。

今回習うのはこんな形↓

$$ y= \frac{10}{x} \qquad y=-\frac{3}{x} \quad \ldots $$

つまり \(y= \frac{a}{x}\) （ \(a\) には数字が入る）の形の関数を反比例という。

んで、こういう形の関数式なら「 \(y\) は \(x\) に反比例する」という。

逆に、\(y\) が \(x\) に反比例するなら、式の形は「 \(y= \frac{a}{x}\) 」ってこと。

（ちなみに \(a\) に入る数字は反比例の場合でもやっぱり「比例定数」という。）

[前の記事]→「比例と反比例」③　比例の式を求める

 

２．では、反比例の式を求める問題も解いてみよう。

例６）\(y\) は \(x\) に反比例し、\(x=3\) のとき \(y=-8\) である。\(y\) を \(x\) の式で表せ。

比例のときと同じく、\(a\) に入る数字（＝比例定数）さえわかればいい。

そして比例のときと同じように、求め方も２通りある。

ひとつは「代入」を使ったやり方だ。つまり、

\(y= \frac{a}{x}\) の \(x\) と \(y\) に数字を代入して \(a\) を求める方法。

ようするに \(x\) の代わりに \(3\) 、\(y\) の代わりに \(-8\) を当てはめてやる。選手交代だ。

 

３．\(a\) の方程式になった。

分数があるけど、解けるよね。

\(a\) が \(-24\) だとわかったので、最後、式に当てはめて、

$$ y= -\frac{24}{x} $$

これが答え。

ちなみに \(y= \frac{-24}{x}\) じゃ形がヘンなので、マイナスは分数の前に出しておくこと。

（分数まじりの方程式が解けない場合はこちらの記事を参照↓）

中１「１次方程式」でつまずく原因と解決法①　導入

 

４．おなじ方法で、例題７も解いてみよう。

例７）\(y\) は \(x\) に反比例し、\(x=4\) のとき \(y= \frac{7}{2}\) である。\(y\) を \(x\) の式で表せ。

解）\(y= \frac{a}{x}\) に \(x=4\) 、\(y= \frac{7}{2}\) を代入して、

\begin{eqnarray} \frac{7}{2} &=& \frac{a}{4} \\ \frac{a}{4} &=& \frac{7}{2} \\ a&=& 14 \end{eqnarray}

$$ y= \frac{14}{x} $$

このように、反比例の式に代入して比例定数 \(a\) を求める。

これがひとつめの方法。

 

 

指導案（後半）

５．そして、比例定数を求める方法はもうひとつある。

ヒントはこれ。

例６）\(x=3\) 、\(y=-8\) ⇒比例定数 \(a=-24\)

例７）\(x=4\) 、\(y=\frac{7}{2}\) ⇒比例定数 \(a=14\)

気づいた？

$$ a=xy $$

これが反比例で、\(a\) を求める裏ワザ。

 

６．この裏ワザを使って、例題８を解いてみよう。

例８）\(y\) は \(x\) に反比例し、\(x=\frac{5}{6}\) のとき \(y= \frac{12}{5}\) である。\(y\) を \(x\) の式で表せ。

解）

$$ a= \frac{5}{6} \times \frac{12}{5} = 2 $$

$$ y= \frac{2}{x} $$

早いでしょ？

イッパツで出るでしょ。

この例題８を、もし代入する方法でやろうと思ったらタイヘンだ。

だから、この裏ワザ、どんどん使いましょう。

 

７．ここまでをまとめよう。

反比例の式を求める問題では、

○ \(y= \frac{a}{x}\) の \(x\) と \(y\) に数字を代入して \(a\) を求める。

○ \(a=xy\) を使って \(a\) を求める。

この２つの方法があるということ。

そしてふたつめの方法がおすすめだということ。

 

じゃ、たくさん問題を解いて「わかる」を「できる」にしていこう。

 

 

注意点

比例の式を求める場合とおなじく、ひとつめの注意点は、

「逆に、\(y\) が \(x\) に反比例するなら、式の形は『 \(y= \frac{a}{x}\) 』」

この一言を忘れないことです。

両方がともに必要十分条件であることを示してはじめて、問題を解くことが論理的に可能になるからです。

学校の先生も、塾講師や家庭教師の方も、この一言は意外と忘れがちです。

というか、中１数学の教科書にもこの一言は載っていません。

文科省と各出版社の手落ちじゃないか…。

 

もうひとつの注意点は、

「 \(a=xy\) を使って \(a\) を求める。」

この方法もきちんと薦めることです。

なぜならこっちの方法を使うことではじめて、例題８のような、つまり分数が出てくるような問題も解けるようになるからです。（ちなみに公立中学では繁分数を習わない）。

とくに、次のような問題が出たときには \(a=xy\) を使うしかありません。

類題）\(y\) は \(x\) に反比例し、\(x=\frac{1}{6}\) のとき \(y= \frac{1}{5}\) である。\(y=2\) のときの \(x\) の値を求めよ。

解）

$$ a= \frac{1}{6} \times \frac{1}{5} = \frac{1}{30} $$

よって、 \(a=xy\) に \(a= \frac{1}{30}\) 、\(y=2\) を代入して

\begin{eqnarray} \frac{1}{30} &=& 2x \\ 2x &=& \frac{1}{30} \\ x &=&  \frac{1}{60} \end{eqnarray}

この問題は、次で解説する応用問題のさらに発展版ともいえるものです。

詳しくは語りません、みてわかるとおりです。

\(a=xy\) を知っていればかんたんに解けるんです。

 

だからこそ、反比例における比例定数の求め方は２通りとも指導する。

現行の教科書では必修知識でないけれど、\(a=xy\) の方法もちゃんと教える。

これが後々、生徒のためになると私は考えます。

 

 

反比例の式を求めてさらに…

 

指導案

１．では、反比例の式を求める問題の応用編。

例９）\(y\) は \(x\) に反比例し、\(x=4\) のとき \(y=-12\) である。\(x=16\) のときの \(y\) の値を求めよ。
（2017山梨県公立高校入試問題）

コツは、比例のときと一緒だ。

問題を前半と後半に分ければいい。

つまり、

例９の前半： \(y\) は \(x\) に反比例し、\(x=4\) のとき \(y=-12\) である。（ \(y\) を \(x\) の式で表せ。 ）

例９の後半：（出てきた式において、） \(x=16\) のときの \(y\) の値を求めよ。

 

２．例９の前半を解くとこうだ。

んで、例９の後半を解くとこうだ。

このように、問題を前後半で分ければぜんぜん難しくない。

 

３．んで、じつは、反比例の式を求める問題の応用編には、もうひとつ解き方がある。

ほとんど同じ解き方なんだけど、ちょっとちがう。

どこがちがうか、よーく見て気づいて。

例９）\(y\) は \(x\) に反比例し、\(x=4\) のとき \(y=-12\) である。\(x=16\) のときの \(y\) の値を求めよ。
（2017山梨県公立高校入試問題）

別解）

$$ a=4 \times (-12) = -48 $$

よって、\(a= xy\) に \(a=-48\) 、\(x=16\) を代入して、

\begin{eqnarray} -48 &=& 16y \\ 16y &=& -48 \\ y &=& -3 \end{eqnarray}

答．\(y=-3\)

\(a=-48\) と求めるところまでは同じだね。

ちがうのはそのあと。

反比例の式 \(y= – \frac{48}{x}\) に \(x=16\) を代入するんじゃなくて、

\(a=xy\) って式、つまり \(-48=xy\) に \(x=16\) を代入する。

つまり \(a=xy\) の式だけ使うやり方。

前半で比例定数を求めるときと、後半で代入するとき、あわせて２回とも \(a=xy\) を使うやり方。

 

この方法のメリットは、分数が出てこない点。

反比例の式って、もともと分数で、しかも分母に \(x\) があるやん？

それ、なんかイヤって人には、こっちの方法がおすすめです。

 

４．じゃ、例10を２通りの方法で解いてみるね。

まず最初の方法で解くと、こうだ。

例10）\(y\) は \(x\) に反比例し、\(x= \frac{10}{3}\) のとき \(y=- \frac{12}{5}\) である。\(x=\frac{1}{2}\) のときの \(y\) の値を求めよ。

解）

$$ a=\frac{10}{3} \times \left( -\frac{12}{5} \right) = -8 $$

よって \(y= – \frac{8}{x}\) に \(x=\frac{1}{2}\) を代入して、

\begin{eqnarray} y &=& -\frac{8}{\frac{1}{2}} \\ y &=& -8 \div \frac{1}{2} \\ y &=& -8 \times 2 \\ y &=& -16 \end{eqnarray}

答．\(y=-16\)

途中、分数のなかに分数が出てきた。

「は？何コレ！？」ってなるけど、分数は上÷下に直せたよね。

$$ \frac{7}{4}= 7 \div 4 $$

この考え方を使って乗り切りました。

ただまぁ、式はごちゃごちゃする。

 

５．次に、例10をもうひとつの方法で解くと、こうだ。

例10）\(y\) は \(x\) に反比例し、\(x= \frac{10}{3}\) のとき \(y=- \frac{12}{5}\) である。\(x=\frac{1}{2}\) のときの \(y\) の値を求めよ。

別解）

$$ a=\frac{10}{3} \times \left( -\frac{12}{5} \right) = -8 $$

よって、\(-8= xy\) に \(x=\frac{1}{2}\) を代入して、

\begin{eqnarray} -8 &=& \frac{1}{2}y \\ \frac{1}{2}y &=& -8 \\ y &=& -16 \end{eqnarray}

答．\(y=-16\)

これが \(a=xy\) の式だけを使うやり方。

（途中の日本語で、\(a=-8\) はもう代入しといた）。

別解のほうがラクだと先生は思うけど、自分が「確実だ」と思うほうの方法で、解きましょう。

 

６．これで応用問題も終わり。

まとめるよ。

○コツはやはり問題を前半と後半に分けること。

○後半は２通りの方法がある。

$$ y=\frac{a}{x} \mbox{の式に代入する} $$

$$ a=xy \mbox{の式に代入する} $$

以上が、反比例の式を求める応用問題の、解き方のコツ。

ではたくさん問題を解いて「わかる」を「できる」にしていくこと。

 

 

注意点

「応用問題でも解法を２通り教えるのか。生徒の負担にならないか」。

こんな疑問を抱く方もあるかもしれません。

結論をいうと、生徒の負担にはぜんぜんなりません。

むしろ子どもというのは解き方をたくさん知れば知るほど喜んで使います。

だって、たくさん解き方を知るほど解ける問題が増えるから。

何百人、何千人の生徒と接するうち、負担に思っていたのは大人であるわたしのほうだったと気づきました。

かんたんに解ける方法があって、その方法に頼ることがのちの学習の妨げにならないなら、使わない手はない。

だから数学が苦手な子も、偏差値60以上の高校をねらう子も関係ありません。

解き方はちゃんと全部伝えてあげましょう。

 

もうひとつの注意点は、比例の記事からくりかえし言ってきましたが、

「 \(y= – \frac{48}{x}\) に \(x=16\) を代入して」

「 \(-8= xy\) に \(x=\frac{1}{2}\) を代入して」

こうした一文を書かせること。

そして、比例定数の求め方は

$$ a=xy $$

こっち優先で使わせることです。

理由は、やはり比例の記事のくりかえしになりますが、こんな問題が正確に・スラスラと解けるようにするためです。

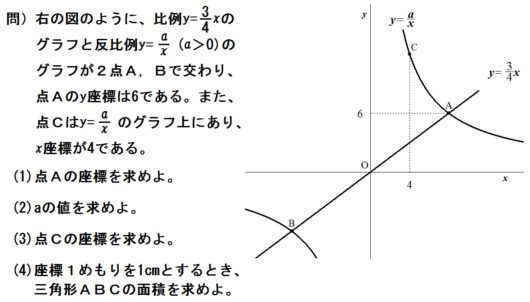
(1)A（8,6）  (2) a=48  (3)Ｃ（4,12）  (4)72㎠

(4)の解き方は「比例と反比例」⑤　参照

なので、「比例と反比例の式を求める」単元すべてにおける指導上の注意点。

それは

• 代入という操作を正しくできるように、解法途中の日本語も書かせる。
• 比例定数のかんたんな求め方をちゃんと教える。

この２点であるといえます。

 

 

まとめ

以上、反比例の式を求める問題の指導方法と注意点でした。

 

この記事のまとめ

反比例の式を求める問題ができない・わからない原因もやはり３つ。

①反比例の式 \(y=\frac{a}{x}\) をおぼえていない

②代入という操作が正しくできない

③ \(a=xy\) を知らない

 

よってまず反比例の式をいろいろ示す。

そして、\(y\) が \(x\) に反比例するなら式の形は「 \(y=\frac{a}{x}\) 」だとも付け加える。

 

こうした基本問題を解く方法は２つ。

① \(y=\frac{a}{x}\) の \(x\) と \(y\) のところに数字を代入して \(a\) を求める。

② \(a=xy\) を使って \(a\) を求める。

方法①を使う際には「…に～を代入して」という一文を書かせること。

 

こうした応用問題では、問題を前半と後半に分けることがコツ。

前半は \(a=xy\) を使ってパッと解くこと。

そして後半では、

$$ y=\frac{a}{x} \mbox{の式に代入する} $$

$$ a=xy \mbox{の式に代入する} $$

という２通りの方法があることを伝える。

 

 

余談ながら…

ジュウゴの経験上、比例・反比例の単元というのは簡単な部類に入ります。

つまずく生徒はほとんどおらず、問題もよくできていく。

ただ中２、中３から指導する生徒のなかに、この比例・反比例でつまずいたという中学生が多い。

これは学校での教え方がまずいためと考えています。

何がまずいのか？

上記３点の原因を解決することなく、「比例・反比例の意味」をやたら考えさせたり、いきなり具体例の難問を与えて「自分で考える姿勢を身につけさせよう」としすぎることです。

これは学校の先生が悪いのではなく、指導要領がそうなっているから。

そして指導案の素材を考える人が現場を知らない大学教授だからです。

 

さいわい、2021年度から全面実施される中学の新学習指導要領では、すこし改善されます。

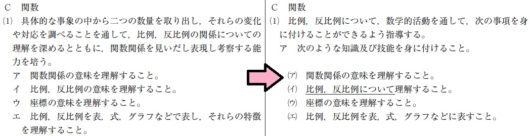
新指導要領の「第１学年 関数」では、以下の文面が削除されます。

そして、身につけるべき力も以下のように変更になります。

 

 

 

何が言いたいのかというと、数学の指導でいちばん大切なのは問題を解けるようにすることだって言いたいのです。

意味とか、理解を深めるとか、考える姿勢だとか、よくわからない漠然とした概念に教育者は囚われがちです。

とくに大学で教育論を学んで新卒で入った学校教員ほど、その傾向が強くあります。

子どもがいちばん喜ぶのはどんなときか？

よーく子どもを観ていればおのずとわかります。

もし、この記事を読んでいる教員がおられたら、気に留めていただきたい。

現場を知らない大学教授がつくる指導案よりも、目の前の子どもからの気づきをいちばん大切にしてください。

子どもはきっと、問題が解けたとき、そこでほめられたとき、いちばんヤル気になって目を輝かせるはずです。

そうした子どもの変化こそ、教師にとっていちばんの学びなんです。

 

経験豊富な教師・講師の方には釈迦に説法だったかもしれません。

比例と反比例の単元では、とくにこういう傾向があるので、言わずにおれませんでした。

視力検査とランドルト環の関係？コンタクトとメガネどっちがオシャレか、そっちのほうが大切だ！

ガソリンと走行距離？それよりこの宿題が解けるように教えてくれ！

…

次の座標とグラフでも、子どもから教わった視点で解説していきます。

→中学数学「比例と反比例」⑤　座標とグラフ