中1数学「1次方程式」文章題。
4回目は平均問題の解き方について。
応用や難問になると途端にわからなくなる…
テストの平均点問題が解けない…
こんな中学生に活用ください。
[関連記事]
○文章題④【平均の問題】
まずはじめに、方程式の平均問題でつまずく原因から述べます。
つまずく原因は主に2つ。
ひとつは、平均の公式2つを覚えていない(自由に使えない)こと。
つまり以下の公式を2つとも使えてはじめて平均問題は解けるようになります。
特に、(合計)=(平均)×(数)という公式②を覚えてない生徒が多い。
どちらも覚えて使っていけば、それだけで平均問題の立式はかんたんにできます。
忘れた!という人はいま覚えてください。
つまずく原因のもうひとつは、方程式文章題の手順の最初をとばしているというもの。
つまり「求めるものを \(x\) とする」と、解答の一行目にきちんと書かないせいです。
これがないために、\(x\) を含んだ等式をつくることができなくなっているんです。
文章題は特に応用・難問になるほど、「わからない数量があるけどとりあえず文字で表してみる」という姿勢が重要になります。そうすることで、公式に当てはめたら式が立った!等ということが多々あるからです。
スポンサーリンク
平均の公式を2つとも自由に使えること。
まず最初に未知数を \(x\) と表すこと。
この2点に注意しながら、平均問題をやっつけていきましょう。
*連立方程式の平均問題はこちら
平均問題 基本その一

まずは例題1から。
こんな問題ではそれぞれの値が具体的にわかってます。
よって求めるものを \(x\) とし、あとは平均の公式①に当てはめるだけです。
方程式を立てるときのコツ
例題1)平沢君の数学のテストの点数は、今までの3回が76点、54点、61点だった。次に何点を取れば、4回の平均が65点になるか?
「次に \(x\) 点を取るとする。」
最初に書くべきはこの一文です。
なにはともあれ、求めるものを \(x\) でおくことを、方程式文章題では忘れてはいけません。
意外と中3になってもできていない生徒がいるので、「たまに書き忘れるかも」という中学生は気をつけてください。
さて、4回目が \(x\) 点だったとしたら、点数の合計は
\(76+54+61+x\) です。
また回数はとうぜん \(4\) 回です。
んで4回の点数の平均が \(65\) 点です。
あとはこれらを平均の公式①に当てはめるだけですね。
$$ \frac{76+54+61+x}{4} =65 $$
これが例題1の方程式になります。

あとは方程式を解いて、確かめて、単位をつけて答えを書く。
最後までやると以下のとおりです。
解)次に \(x\) 点を取るとする。
\begin{eqnarray} \frac{76+54+61+x}{4} &=& 65 \\ 76+54+61+x &=& 65 \times 4 \\ x &=& 260-191 \\ x &=& 69 \end{eqnarray}
答.69点
以上のように、それぞれの値が具体的にわかってる問題では、平均の公式①に当てはめてやるだけで方程式が立ちます。
かんたんですね。
練習問題
では練習問題を2つほど載せます。
解答は末尾に記載、質問はコメント欄からどうぞ。
なお方程式文章題の手順は文章題1回目の記事を参照ください。
問1)A、Bの2人の身長はそれぞれ154cm、159cmである。これにCが加わると、3人の身長の平均が155cmになるという。Cの身長を求めよ。
問2)コロッケ4個の重さを量ったらそれぞれ67g、72g、64g、75gだった。あと1個たして、コロッケ5個の重さの平均を70gにしたい。何gのコロッケをたせばいいか。
問1) 152cm
問2) 72g
平均問題 基本その二

次に例題2です。
この問題は例題1と違って、増川君と直井君と升君それぞれの具体的な値がわかりません。
ただ3人の平均は55kgとわかっています。
これを使えば、平均の公式②に当てはめることで、3人の合計が出ます。
そこから方程式を作っていくんです。
方程式を立てるときのコツ
例題2)増川君、直井君、升君3人の体重の平均は55kgである。これに藤原君が加わると4人の体重の平均は53kgになる。藤原君の体重を求めよ。
「藤原君の体重を \(x\) kgとする。」
何度も言いますがこの一文を忘れずにね。
つぎに方程式を立てていきますが、増川君、直井君、升君それぞれの具体的な体重がわかりません。
しかし3人の体重の平均は55kgとわかってます。
ここで平均の公式②を使うわけです。

3人の体重の合計は \(55 \times3\) と出ます。
よって藤原君を加えた4人の合計は
\(55 \times3 +x\) と表せます。
また人数は \(4\) 人、その平均は \(53\) kgです。
これらを、平均の公式①に当てはめることで、方程式が立つ。
つまりこれ。
$$ \frac{55 \times3 +x}{4} =53 $$
あとはこの方程式を解いて、確かめて、単位をつけて答えを書くだけですね。
解)藤原君の体重を \(x\) kgとする。
\begin{eqnarray} \frac{55 \times3 +x}{4} &=&53 \\ 165+x &=& 53 \times4 \\ x &=& 212-165 \\ x &=& 47 \end{eqnarray}
答.47kg
以上のように、それぞれの具体的な値がわからないけど平均はわかっている場合、公式②を使って部分的な合計が出せる。
あとは公式①にそれぞれ当てはめて方程式をつくる。
こうして段階をふんで立式していくといいでしょう。
問題の解釈としては、「増川君、直井君、升君みんな55kgとみなしていい」ってことです。
それが平均の意味でもあるからね。
練習問題
では練習問題です。
質問はコメント欄からどうぞ。
問3)A、B、C3人の走り幅とび記録の平均は4.2mだった。次にDがとんだら、4人の記録の平均が4.5mになった。Dは何mとんだか。
問4)秦君はこれまで何回か数学のテストを受けて、いままでの平均点が75点だった。もし次のテストで90点をとれば、平均点は80点になるという。秦君はいままで何回のテストを受けてきたか。
問3) 5.4m
問4) 2回
平均問題 応用

最後に、平均問題の応用・難問でもっともよく出題されるものを。
いわゆる「クラスでのテストの平均点問題」です。
この平均点問題もいままでの知識を応用するだけで解けますが、なにがなにやら整理できず頭の中がごっちゃになって解けないという中学生を多くみかけます。
そこで、平均点問題が出てきたら表を書いて整理することをおススメします。
*連立方程式の平均点問題はこちら
方程式を立てるときのコツ
例題3)あるクラスで数学のテストをしたら、男子24人の平均点は71点、クラス全体の平均点は73点だった。女子16人の平均点を求めよ。
「女子16人の平均点を \(x\) 点とする。」
まずはこれを書きます。忘れずにね。
つぎに方程式をつくりますが、それぞれの人数と平均点を整理するために表を書くといいでしょう。
たとえばこんなの↓
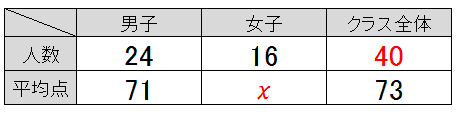
ようするに、男子・女子・クラス全体それぞれの人数と平均点、計6項目を整理する表が作れればいい。
問題文に書いてない項目は計算して埋めるか、あるいは \(x\) を使って表します。
こうして6項目すべてが埋まれば、まず男子の合計点と女子の合計点が出ます。
平均の公式②を使って、
男子の合計点:\(71 \times24\)
女子の合計点:\(x \times16\) です。
ということは、クラス全体の合計点は \(71 \times24 + x \times16\) 。
またクラス全体の人数は \(40\) 人、クラス全体の平均点は \(73\) 点。
よって、これらすべてを平均の公式①に当てはめれば、
$$ \frac{71 \times24 + x \times16}{40} = 73 $$
こうして方程式が立つんです。
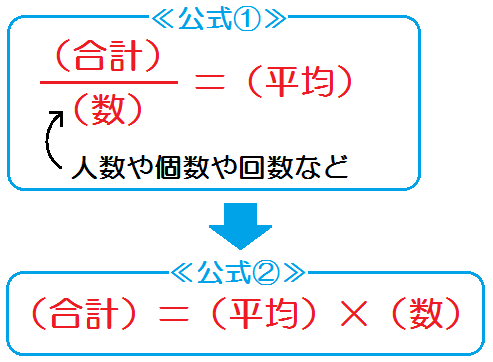
平均の公式
(例題3を最後まで解くと以下のとおり)
解)女子16人の平均点を \(x\) 点とする。
\begin{eqnarray} \frac{71 \times24 + x \times16}{40} &=& 73 \\ 1704 + 16x &=& 73 \times40 \\ 16x &=& 2920-1704 \\ 16x &=& 1216 \\ x &=& 76 \end{eqnarray}
答.76点
同様にして、例題4も求めることができます。
例題4)32人のクラスがある。数学のテストの平均点は男子64点、女子80点、クラス全体では73点だった。男子の人数を求めよ。
まず、男子の人数を \(x\) 人とする。
次に表を埋めて、そんで方程式を立てる。
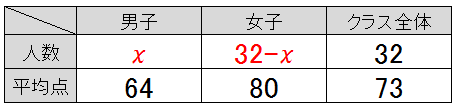
$$ \frac{64 \times x + 80 \times(32-x)}{32} = 73 $$
あとは解いて、確かめて、答えを書く。
\begin{eqnarray} 64x +80(32-x) &=& 73 \times 32 \\ 64x +2560 -80x &=& 2336 \\ 64x -80x &=& 2336 -2560 \\ -16x &=& -224 \\ x&=&14 \end{eqnarray}
答.14人
このように、計6項目の表を書いて整理すれば、クラスの平均点問題もすべて解くことができます。
ちなみに、この例題のような未知数2つの問題は「代金と個数」の記事でやりました。「合計で○ならば一方を \(x\) 、もう一方は ○\(-x\) と表せる」でしたね。
忘れた人は過去記事を参照してください↓

練習問題
「クラスでのテストの平均点問題」は応用範囲が広く、いろんな難問が出題されます。
しかしどの応用問題も、6項目のうちどれかを求める問題にすぎません。
上のように表を書いて整理すれば必ずやっつけられます。おそれず、チャレンジしてみてください。
では練習問題をどうぞ。
(解答は末尾、質問はコメント欄から)
問5)女子が男子よりも2人少ないクラスがある。数学のテストの平均点は男子75点、女子60点、クラス全体では68点だった。男子の人数を求めよ。
問6)男子16人、女子20人のクラスで数学のテストをしたら、クラス全体の平均点は59点で、女子の平均点は男子の平均点より9点高かった。女子の平均点を求めよ。
問5) 16人
問6) 63点
まとめ
≪方程式文章題における平均問題のコツ≫
まず求めるものを \(x\) とおくこと。
これをしないでできない・わからないとなってる中学生も多い。
「わからないけどとりあえず文字で表す」姿勢が数学では重要。
それぞれの値が具体的にわかってる場合は、平均の公式①に当てはめるだけ。
また、具体的な値がわからないけど平均はわかる場合、平均の公式②を使って部分的な合計を出す。
それから公式①に当てはめて方程式を立てる。

平均の公式
クラスの平均点問題もやりかたは同様。
そして整理が難しいときは、表を書いて6項目すべて埋めればいい。
ちなみに未知数2つの問題では一方を \(x\) 、もう一方を \(x\) を使った式、で表す(詳しくは方程式文章題1回目の記事を参照)。

さて、次回は中1方程式文章題の鬼門のひとつ、「過不足の問題」について解説します。
過不足問題をまとめてやっつけるコツがあるんで、ご期待ください。
それが終われば残すは「速さ」「割合」「図形」の3つ。
年内に比例・反比例までいけるんだろか…
[関連記事]





コメント
申し訳ありませんが、問6の問題の答えがどうしても63になりません。
方程式を教えて下さい。お願いします。
平均の問題は、私が教えている生徒の教科書、ワークには出てこないので、教えていないのですが、
もしやったら、彼らのレベルからすると、例題2以降は苦戦しそうです。
それ以前に、公式2を使えないでしょうね。
「3人の体重の平均は55kgである。3人の体重の合計は何kgか求めよ。」
このあたりからやる必要がありそうです。
反転の仕方わかりました〜
ありがとうございます
練習問題の問4の解き方を教えて頂けますか?
下のコメントに対する回答をご覧ください。
ドラッグして反転とはどうすればいいのでしょうか?
女子が男子よりも2人少ないクラスがある。数学のテストの平均点は男子75点、女子60点、クラス全体では68点だった。男子の人数を求めよ。
の答えを教えてください
答えは問題文の一行下をドラッグ・反転させると見えます。
夜分遅くに申し訳ございません。
問5の式を作成する時の場合分母はどうしたら良いでしょうか?
ななしのさん
男子の人数をx人とすると、
女子はx-2(人)なので、
合計人数は合わせて2x-2(人)。
これが分母になります。
つまり方程式は
75x+60(x-2) / 2x-2 =68
両辺に 2x-2をかけて
75x+60(x-2) =68(2x-2)
・・・
ただ厳密には分母が0にならないよう
x≠1とx=1とで場合分けが必要ですが、
中学数学ではそこまでしなくてもOKです。
平均の基本その二の練習問題 問4 の答えが2回とありましたが
その答えになるまでの式がどうしてもわかりません。
教えていただけませんでしょうか。よろしくお願いします。
以下の式になります。
秦君はいままでx回のテストを受けてきたとする。
(75x+90)/(x+1)=80
(左辺は分子が75x+90、分母がx+1)
75x+90=80(x+1) でもOKです。
(x+1)では何故1が付くのですか?
そのままxだけをかけるのではダメなんですか?
夏期講習のため全然ブログに目を通せませんでした、失礼しました。
>けんこさん
たとえば、今まで5回のテストを受けていたら、次のテストを受けたら合計が
5+1
の6回となるからです。