中1数学「空間図形」の4回目。
今回は表面積の求め方を解説します。
流れとしては
- まず基本として、表面積の求め方を確認
- そのなかで円柱と球の表面積もやっちゃう
- つぎに円錐の表面積の求め方をくわしく解説
- 考え方さえマスターすれば、応用問題もできることを共有
- 最後に高校入試から、難問を2つほど
という構成です。
とくに円錐の表面積は中学生がつまずきやすいところなので、わかりやすいコツをお伝えします。
ではいきましょー。
基本:表面積の求め方
立体の表面積とは、表側にある面の面積をすべて足したものをいいます。
イメージとしては、空気にふれてる面ぜんぶってこと。
だから、基本となる求め方は展開図をかいて求めるというものです。
以下、例題とともに見ていきましょう。
角柱の表面積
例題1)下の図は、AB=3cm、BC=4cm、AC=5cm、∠ABC=90°の直角三角形ABCを底面とし、AD=BE=CF=2cmを高さとする三角柱である。この三角柱の表面積を求めよ。
2019 神奈川県公立高校入試問題 6-ア
まず、ノートや余白にこんな展開図をかきます↓
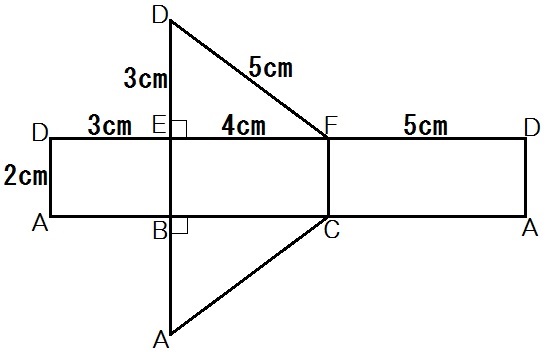
頂点は書いても書かなくてもいいですが、長さはかならず書き込みましょう。
かけたら、5つの面があるとわかりますね。
直角三角形が上下に2つ、中ほどに長方形が3つ。
これらそれぞれの面積を求めます。
暗算でいけるよね!?
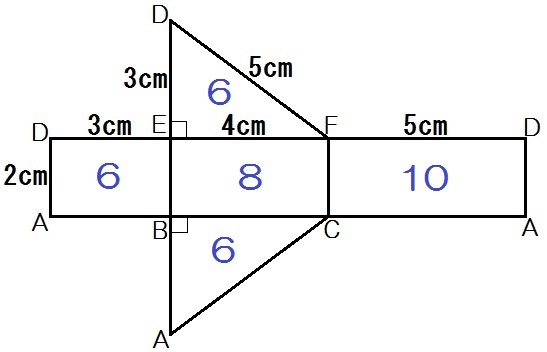
よく間違えるのは、三角形の面積を
\begin{eqnarray} 3 \times 5 \times \frac{1}{2} &=& \frac{15}{2} \quad \mbox{(×)} \\ 4 \times 5 \times \frac{1}{2} &=& 10 \quad \mbox{(×)}\end{eqnarray}
などとしちゃうこと。
底辺&高さって3cm&4cmだから!気を付けて!
さて、それぞれの面積が出たらあとは足すだけです。
\begin{eqnarray} & &6+6+6+8+10 \\ &=& 36 \end{eqnarray}
もちろん、「同じ三角形が2つ」だから×2としてもいいし、中ほどの長方形をひとつの横にながーい長方形とみて求めてもいい。
\begin{eqnarray} & &6 \times 2 \ + \ 2 \times (3+4+5) \\ &=& 12 + 24 \\ &=& 36 \end{eqnarray}
いずれにしても
答.36㎠ と出ます。
*展開図がかけない人はこちらの記事中の「展開図のコツ」を参照↓
空間図形② 位置関係・展開図・回転体のコツ
なお、展開図でなく、面をそれぞれ描く方法もあります。
こんなの↓
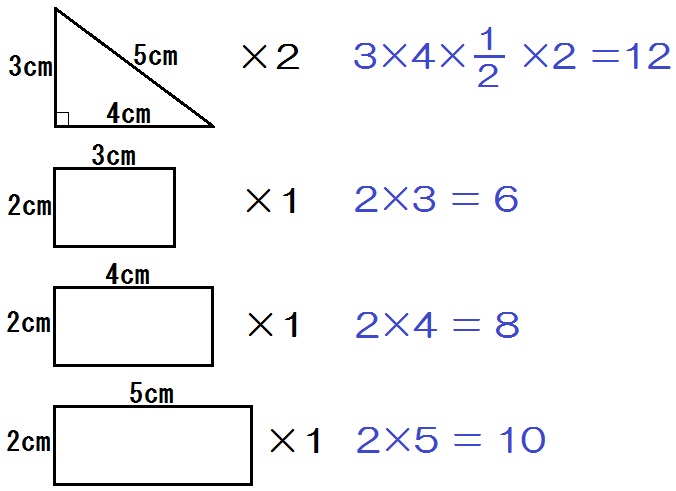
つまり、何種類の面があるか書き出して、それぞれ面積を求めて足すんです。
この方法のメリットは
- 展開図がどんな形かと考えなくていい
- 組み合わせた立体の表面積でも求めやすい
という点があります。ただデメリットとして
- 展開図でやったような計算の工夫ができない
- 数えもれの可能性がある
- 辺どうしのつながりがわからない
という点もある。
とくに3点目は円柱や円錐で大切なので、この記事では展開図をかく方法でいきます。
いずれにしても、表面積の求め方の基本は表側の面をぜんぶ描くということです。
[関連記事]
空間図形① 苦手になる原因と解決方法
角錐の表面積
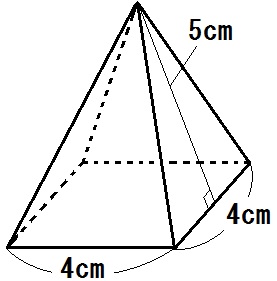
では角柱につづいて、角錐の表面積も求めてみましょう。
やりかたは同じです。
展開図は、たとえばこんなかんじ↓
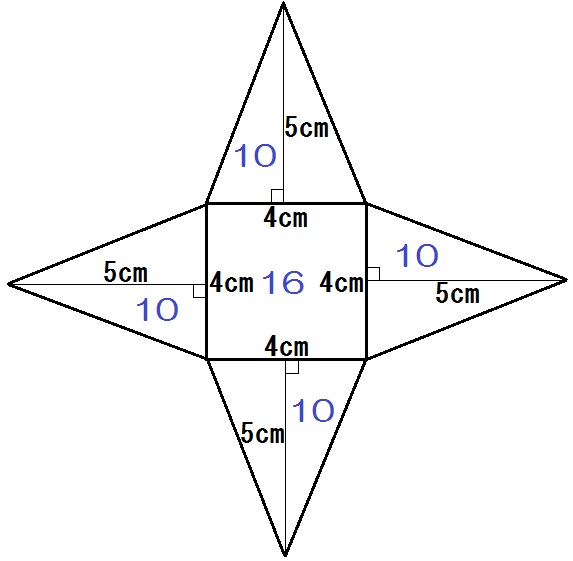
ちなみに、面をそれぞれかく場合はこう↓
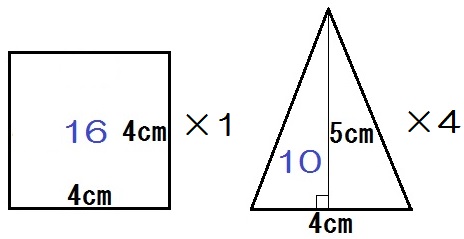
いずれにしても
\begin{eqnarray} & &16 \ + \ 10 \times 4 \\ &=& 56 \end{eqnarray}
答.56㎠と出ます。
表面積の問題は、表面の図をちゃんと描けばむずかしくありません。
さて、ここでちょっと余談。
中1の後半になり、空間図形の体積・表面積問題まですすんできて、気づきましたか?
あるていどの暗算力が求められることに。
たとえば例題2では
$$ 4 \times 5 \times \frac{1}{2} = 10 $$
が暗算でできることが望ましい。
また前回の記事の例題6で
$$ 36 h = 216 – 36 \pi $$
という方程式が出てきましたが、これも \(216 \div 36\) が暗算でできないと、パッと解けません。
中1前半の計算単元でジュウゴがしつこいくらい計算力を強調してきたのは、こういうわけなんです。
もし、いま教えている生徒やお子さんが体積・表面積問題を解くとき、よこにかんたんな計算式を書いているなら、その子はすでに学力が不足していることになります。
ぜひ春休みなどを活用して、暗算力の強化をおこなってください。
ジュウゴも毎年そうしてます。
円柱の表面積
例題3)下の図は、底面の半径が3cm、高さが9cmの円柱である。この円柱の表面積を求めよ。
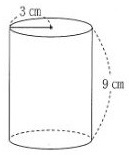
2019 奈良県公立高校入試問題 1-5
つづいて円柱の表面積の求め方です。
まずはやはり展開図をかいてみましょう。
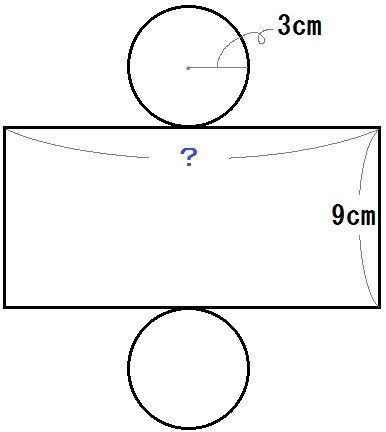
同じ大きさの円が上下に2つと、中ほどに長方形が1つできます。
円の面積は、半径3cmなので、すぐ求まります。
しかし、長方形の横の長さがわからない。
どうしよう?
ここで、展開するまえ、長方形の横の辺はどこと接していたか考えてみてください。
そう、円周ですね。
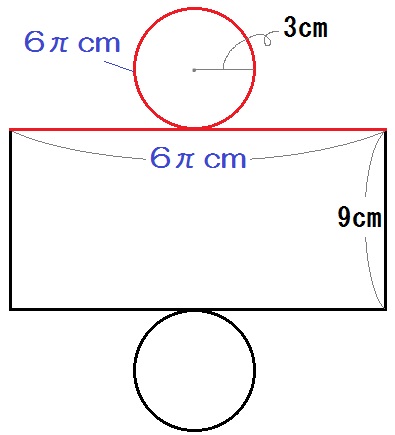
よって長方形の横の長さは、直径×円周率で、\(6 \pi\) cmと出ます。
あとは面を足していくだけ。
\begin{eqnarray} & & 3 \times 3 \times \pi \times 2 \ + \ 9 \times 6 \pi \\ &=& 18 \pi \ + \ 54 \pi \\ &=& 72 \pi \end{eqnarray}
答. \(72 \pi\) ㎠と出ます。
いちおう、式はていねいに書きましたが、円と長方形の面積はもう暗算でいけますね。よって
\begin{eqnarray} & & 9 \pi \times 2 \ + \ 54 \pi \\ &=& 72 \pi \end{eqnarray}
くらいの式でもOKです。
ということで、円柱の表面積もやっぱり展開図をかくこと。
そして円柱の場合「長方形の横の長さ」=「円周の長さ」というところがポイントです。
球の表面積
表面積の求め方の基本、さいごは球の表面積です。
例題4の立体は半径 \(\frac{3}{2}\) cmの球になります。
ただ球の表面だけは、展開図のように平らに伸ばすことができません(ミカンの皮を一回でむいてテーブルに置いても、しわくちゃになる)。
そこで公式の出番。
球の表面積 \(S\) は
$$ S = 4 \pi r^2 $$
覚え方は「心配あるある」または「心配ある事情(二乗)」。
球の体積の公式とあわせて丸々おぼえちゃってください。
さて、例題4の解答は以下のとおり。
\begin{eqnarray} & & 4 \pi \times \frac{3}{2} \times \frac{3}{2} \\ &=& 9 \pi \end{eqnarray}
答. \(9 \pi\) ㎠
≪「空間図形」の記事一覧≫
以上、表面積の求め方の基本でした。
- 展開図をかいて求める
- 球だけは \(4 \pi r^2\) に当てはめる
この知識をもとに、円錐の表面積や高校入試の難問をやっつけていきます。





コメント
円錐では、円周と円弧が等しい、という考え方が大切なのはその通りだと思いますが、それを理解した上で、Θ=r1/r2×360゚は使えるようにした方がよいと思います。計算を簡単にするために。
最後のコップを転がす問題も、単純に、9回回転して一周(360゚)するのだから、単純に、360゚×1/9でよいのでは。
なお、最後のコップの問題は、実際には続きがあるんですよね?
上の問題では使わない条件があるので、惑わされる人がいるのではと思いました。
円錐の側面積 半径×母線×π ←これはいい
円錐の表面積 半径×(半径+母線)×π ←混乱します。
単純に
表面積=(側面積)+(底面積)
=(半径×母線×π)+(半径の二乗×π)
で解く方法ではいけないのでしょうか?
混乱するならその方法でもいいと思います。
この記事でジュウゴが言いたかったことは「公式に頼っていては円錐の応用問題が解けない」ということなので、ぶっちゃけ公式などどうでもいいんですが、いちおうの流れで公式っぽく単純な形にして紹介したまででした。