中学数学「1次方程式」の3回目。
今回から2回にわたり、かっこ、小数、分数のある計算問題について解説します。
[関連記事]
それぞれの解き方はむずかしくありません。
かっこのある方程式は、分配法則でかっこを外し、あとは基本の計算です。
\begin{eqnarray} 2x-3(4x-5) &=& x-7 \\ 2x-12x+15 &=& x-7 \\ 2x-12x-x &=& -7-15 \\ -11x &=& -22 \\ x &=& 2 \end{eqnarray}
小数のある方程式は、両辺に10倍、100倍…して小数をなくし、あとは基本の計算です。
\begin{eqnarray} 1.2x-3 &=& 0.45x+6 \\ 120x-300 &=& 45x+600 \\ 120x-45x &=& 600+300 \\ 75x &=& 900 \\ x &=& 12 \end{eqnarray}
分数のある方程式は、両辺に最小公倍数をかけて分数をなくし、あとは基本の計算です。
\begin{eqnarray} \frac{1}{2}x -\frac{2}{3} &=& \frac{3}{4}x +\frac{5}{6} \\ 6x-8 &=& 9x+10 \\ 6x-9x &=& 10+8 \\ -3x &=& 18 \\ x &=& -6 \end{eqnarray}
……と、ここまではよくある解説ですが、この記事を読んでいる人はこういうのを求めてるわけじゃないですよね。
「やりかたはわかってる、でも実際に解こうとするとできないんだ」
「かっこや小数や分数があると、どうしても計算ミスしてしまうんだ」
こういう生徒に出くわしたとき、どう解決してあげればいいか。
それを具体的に提案するのがこの連載です。

そこで、「わかるけど、できない」という子にはどんな原因があるのか?
また、その原因を取り除くためにはどんな指導法がいいのか?
かっこ・小数・分数と3つそれぞれ解説していきます。
数学教員の方、塾講師や家庭教師の方、また中学生をもつ保護者の方。
子どもが以下のどのパターンに当てはまるのかを思い返しつつ、参考にしていただければ幸いです。
スポンサーリンク
かっこのある問題でつまずく
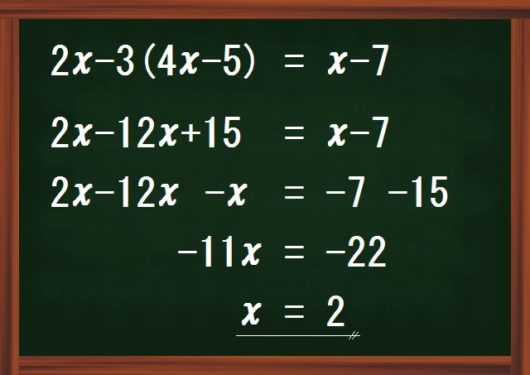
中学数学「1次方程式」のかっこの問題でつまずく原因は、次の2つです。
- 文字式の分配法則の計算ができない
- 3つ以上の項の加減計算ができない
それぞれ具体例と解決案を提示していきます。
分配法則でミス
分配法則でかっこを外すとき、たとえばこんな計算ミスをする中学生がいます。
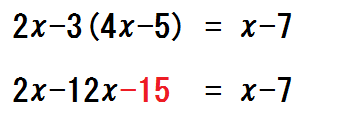
分配法則のミス
こうした計算ミスには、2つの原因が考えられます。
- 「\(-3\)」をかたまりとして捉えられていない
- 符号決定と数字のかけ算の同時処理が苦手
そこで、こんな計算ミスをする生徒には、以下のように指導するといいでしょう。
①式に印を書く
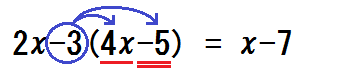
図のような印を書き加えて、符号と数字はひとかたまりだとイメージさせる。
よく間違える生徒には、自分で解くときも印を書くように指導する。
慣れるまで、継続すること。
なお「+」「-」は必ず「プラス」「マイナス」と読ませること。
②符号→数字→文字の順で計算
先生「\(-3 \times 4x\) 、符号はどっち?」
生徒「マイナス」
先生「数字はいくら?」
生徒「\(12\)」
先生「最後に文字を付ける。つまり?」
生徒「\(-12x\)」
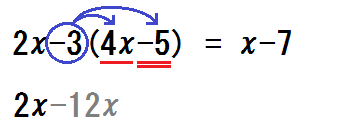
先生「次に \(-3 \times -5\) 、符号はどっち?」
生徒「プラス」
先生「数字は?」
生徒「\(15\)」
先生「つまり?」
生徒「\(+15\)」
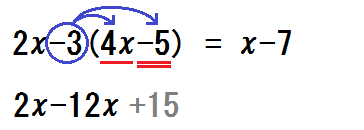
このように「符号→数字→文字」の順で決定していくことを意識させる。
慣れるまでは、発問してあげること。
また生徒が自分で解くときにも意識するように指導すること。
③文字式の分配計算を復習
①②でもダメなら、「文字と式」単元の分配法則を使った計算問題を復習する。
なお、文字式の分配法則の指導については過去記事を参照↓

3つ以上の項でミス
かっこは正しく外せる。
移項もだいじょうぶ。
でも3つ以上の項の加減計算でミスをする中学生もいます。
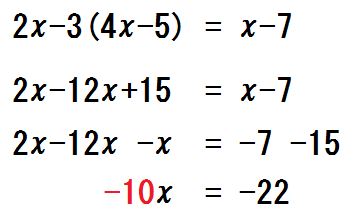
3つ以上の項でミス
考えてみたら、文字式の導入でも、1次方程式の基本でも、3つ以上の項の計算がある問題というのはあまり出題されません。
正負の数:加減で中1の5月頃に習ったきり、という中学校もあるでしょう。
それが夏休みを終えて2学期になって、方程式の応用問題としてかっこを外したら、3つ以上の項の計算がいきなり出てくる。
「どう計算するんだっけ?」と忘れている生徒がいても仕方ありません。
そこで、3つ以上の項の加減で計算ミスをする生徒には、やり方をカンタンに復習するといいでしょう。
〇方法1:前から順番に
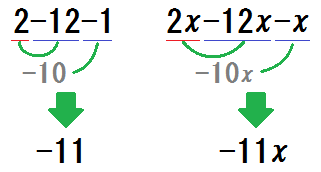
類題として
\(9-45-90\) 、
\(-10x+x-10x+x\) なども。
〇方法2:同符号を先にまとめる
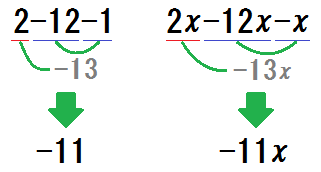
類題として
\(9-45-90\) 、
\(-10x+x-10x+x\) なども。
なお、学校や問題集によっては、かっこのある方程式でも、3つ以上の項の計算問題が出題されない場合があります。
$$4(2x-3)=5(x-6)$$
こんな問題なら、計算する項は2つずつだからです。
しかし、ここであえて3つ以上の項計算をさせておいたほうがいい。
なぜなら、このあとの文章題で以下のような問題が出てくるからです。
→詳しくは1次方程式文章題③「整数・自然数」を参照
文章問題なのに、式を立てたあとの解き方でつまずく。
そんなことのないように、ここで3つ以上の項計算もできるようにしておきましょう。
小数のある問題でつまずく
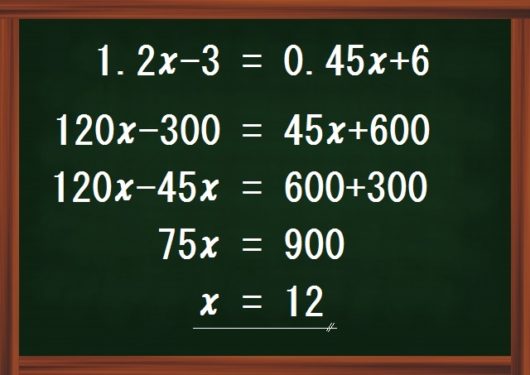
次に、小数のある問題でつまずく原因とその解決法について。
中学数学「1次方程式」の小数の問題でつまずく原因は、以下の3つです。
- 項すべてに10倍、100倍…することを忘れる
- 10倍、100倍…するときに、位をまちがえる
- 「小数×かっこ」だと、両方に10倍、100倍…してしまう
順に見ていきましょう。
10倍、100倍…忘れのミス
とくに小数と整数がまじった方程式の場合、こんな計算ミスをする中学生がいます。
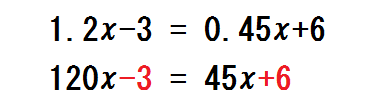
10倍、100倍…忘れのミス
これは、整数項を100倍することを忘れているというミスです。
このように項すべてに10倍、100倍…することを忘れてしまう場合はどうすればいいか?
横に何倍するかをちいさく書かせる。
そして項すべてに下線を引かせるといいでしょう。
①何倍するかを横に書く
両辺を何倍したらいいか聞き、「100倍」と生徒が答えたら、方程式の横に小さく「\( \times 100\)」と書く。
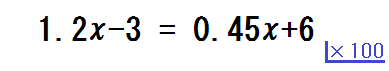
慣れるまで、このように書いてもいいと伝える。
②項すべてに下線を引かせる
次に、方程式の項すべてに下線を引かせる。
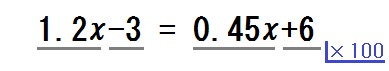
そして「4つぜんぶに \( \times 100\) をする」と伝え、発問しながら次の式の項をひとつひとつ書かせていく。
先生「\(1.2x \times 100\) ?」 生徒「\(120x\)」
先生「\(-3 \times 100\) ?」 生徒「\(-300\)」
先生「\(0.45x \times 100\) ?」 生徒「\(45x\)」
先生「\(+6 \times 100\) ?」 生徒「\(+600\)」
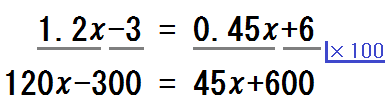
③念押し
とくに整数は10倍、100倍…するのを忘れやすい。
だから間違えなくなるまで、横に何倍するかを書く。
位をまちがえるミス
以上のようなミスは、小数のある方程式ではかなり見かけます。
そして以下のような計算ミスも、同様にかなり見かけます。
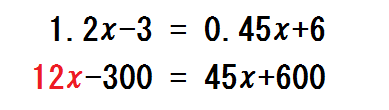
つまり \(1.2x \times 100=12x\) と位をまちがえるミスです。
他にも
$$0.3x \times 100=3x \qquad 4.56 \times 1000=456$$
など、(小数)×10、100…の計算で位をまちがえてしまう。
これは、小数点の位置にたいする不注意が原因です。
そこで、ここでも、何倍するかを横にちいさく書かせること。
そして、小数点の位置がいくつずれるかビジュアルで示すこと。
この2つを意識した指導をおこなうといいでしょう。
①何倍するかを横に書く
両辺を何倍したらいいか聞き、「100倍」と生徒が答えたら、方程式の横に小さく「\( \times 100\)」と書く。
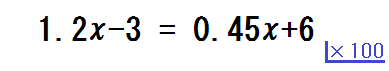
慣れるまで、このように書いてもいいと伝える。
②小数点の位置をビジュアルで示す
余白に「\(1.2\)」と書き、「100倍したら小数点は何個ずれる?」と聞く。
生徒が「2個」と答えたら、以下のように書きくわえる。
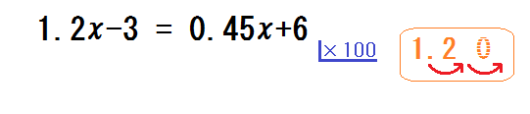
先生「じゃ、\(1.2x\) の100倍は?」
生徒「\(120x\)」
以下同様にして、項をひとつずつ100倍していく。
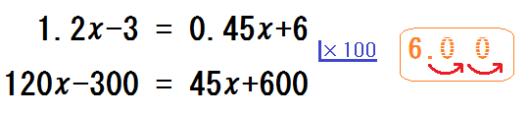
なお、慣れてきたら余白にはもう書かせずに暗算させること。
また、項を意識させるため、上で述べたように下線を引かせてもいい。
![]()
「小数×かっこ」の項でミス
最後に、「小数×かっこ」の項がある問題での計算ミスについて。
\begin{eqnarray} 0.2(3x-4) &=& 0.5x+1.6 \\ 2(30x-40) &=& 5x+16 \end{eqnarray}
このように、「\(0.2(3x-4)\)」を「\(2(30x-40)\)」と、どちらも10倍してしまう。
こんな計算ミスをする中学生もいます。
\(0.2(3x-4)\) はこれでひとつの項です。
よって、\(0.2\) か \( (3x-4) \) 、どちらか片方だけ10倍すると伝えましょう。
ただ、こう伝えると、以下の疑問を抱く生徒もいます。
「なぜ片方だけしか10倍しちゃだめなのか。なんでかっこの中を10倍しないのか」。
これは数学の基本計算にかかわる、とてもいい疑問です。
そこで、こんな疑問を抱いた中学生には、なぜ片方だけ10倍するのかの説明をするといいでしょう。
ちなみにジュウゴは以下のような教え方をします。
説明方法はいろいろありますが、とにかくかけ算でつながったひとつの項を10倍、100倍…するときには片方だけにかけること。
これが腑に落ちたら、以下のような問題も解けるようになるはずです。
$$ 0.7(1.3x-0.4) = 0.2x-0.5 $$
この両辺を10倍しただけでは、かっこの中の小数が消えません。
$$ 7(1.3x-0.4) = 2x-5 $$
よって、さらに両辺10倍して、今度は \( 7(1.3x-0.4) \) のかっこの方にかける。
$$ 7(13x-4) = 20x-50 $$
これでやっと小数が消えるんです。
慣れてきたら、いきなり両辺に100倍して小数を消してもかまいません。
いちおう、頭からおしまいまでの解法はこんな感じですね。
\begin{eqnarray} 0.7(1.3x-0.4) &=& 0.2x-0.5 \\ 7(13x-4) &=& 20x-50 \\ 91x-28 &=& 20x-50 \\ 91x-20x &=& -50+28 \\ 71x &=& -22 \\ x &=& -\frac{22}{71} \end{eqnarray}
こうした問題は難問の部類に入りますが、できなくてよい問題ではありません。
偏差値50以上の高校であれば、高1の段階から「できて当たり前」と扱われるでしょう。
よって、よほど数学につまずいている生徒でない限り、中学生のうちにできるようにしてあげてください。
次の記事→中学数学「1次方程式」④ 分数
まとめ

以上、中学1次方程式のかっこ・小数でつまずく場合の原因と指導法でした。
まとめます。
≪かっこのある方程式でつまずく≫
分配法則でかっこを外すときにミスする場合…
〇式に印を書き加えて、符号と数字はひとかたまりだとイメージさせる
〇「符号→数字→文字」の順で計算することを徹底
*それでもダメなら、文字式の分配計算を復習する。
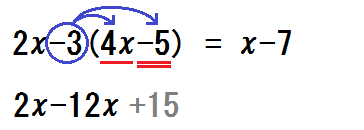
3つ以上の項の加減計算でミスする場合…
〇方法1:前から順番に
〇方法2:同符号を先にまとめる
*このあとの文章題も見据えて、ここはできるようにしておく。
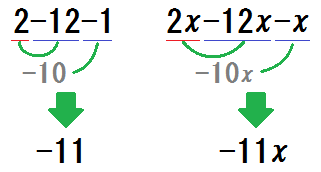

≪小数のある方程式でつまずく≫
整数項に10倍、100倍…することを忘れる場合…
〇横に何倍するかを小さく書く
〇項すべてに下線を引く
*間違えなくなるまで、生徒自身にさせること。
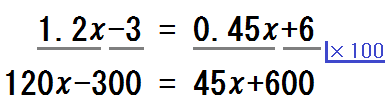
10倍、100倍…したときに位をまちがえる場合…
〇何倍するか書く、項すべてに下線を引くはここでも有効
〇加えて、小数点がいくらズレるかビジュアルで示す
*間違えなくなったら、暗算に移行すること。
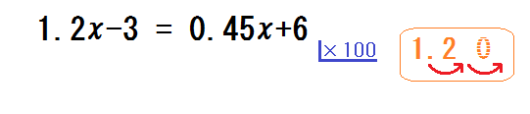
「小数×かっこ」の項を両方10倍してしまう場合…
〇ひとつの項なので、どちらか片方だけ10倍する
〇なぜ片方だけか疑問に思う場合はわかりやすく説明
*偏差値50以上の高校を狙う生徒には、応用として、以下のような問題もできるようにしておくこと。
$$ 0.7(1.3x-0.4) = 0.2x-0.5 $$
次回はこの続きとして、分数のある方程式でつまずく場合の教え方を解説します。
分数まじりの1次方程式でつまずく原因は、主に5つあります。
ひとつひとつ、具体的な解決法があるので、ご参考ください。
それが終わればいよいよ文章題の予定です。
(数学指導法の記事一覧はまとめページへ)



コメント
ありがとうございます!
これを見つけておかんに見せたら
丁寧に教えてくれるように
なりました!
今回も大変参考になりました。
式に印を書く、横に何倍するのか書く、といった工夫を生徒に紹介するのですが、
書くのが面倒くさいのか、なかなか実践してくれません(そして、計算ミスをします)。
私自身は、とても良い方法だと思うのですが、
その効果を、生徒にも実感させることが課題です。
>書くのが面倒くさいのか、なかなか実践してくれません(そして、計算ミスをします)。
いますね、こんな子(-_-;)
解決策としては、くりかえし手元指導する。
正解したら即座にほめる、などでしょうか。
それでも定着しない子は、ジュウゴは放っておきます。
あまりしつこいとヤル気が損なわれるので。
「この子の選んだ決断だ」と、本人の人格を尊重したほうが、結果としてうまくいく場合が多いようです。
ヤル気の仕組みについては以下の記事でも書きましたのでご参考になれば。
→[関連記事]高校受験を控えたわが子に、親ができる4つのこと