中学数学「文字と式」でつまずく原因と解決法⑤　規則性の問題

中１数学「文字と式」の５回目。

今回は文字式単元の最後に、規則性の問題について解説します。

「規則性の見つけ方がわからない」

「なにかうまいコツはないのか」

そんな中学生向けに、規則性の問題がイッパツで解ける方法を紹介します。

ここでつまずいている生徒の指導に、お役立てください。

[関連記事]

○文字と式①：計算の導入

○文字と式②：途中式と分数、かっこ外し、分配法則

○文字と式③：分数まじりの複雑な計算

○文字と式④：数量の表し方

 

こんな規則性の問題は、さまざまな教え方があって、講師の側もどのように指導したらいいのか悩みます。

しかし安心してください。

規則性の指導法は、大別すると３つだけです。

それぞれの方法がどのようなものか？

そして、どんな生徒にどの方法が適しているのか？

つまずく原因とあわせて、くわしく見ていきましょう。

裏ワザのようにイッパツでできてしまう方法も、２つめと３つめに紹介します。


スポンサーリンク

規則性の問題の解き方

規則性の問題は、中学数学ではじめて出あう難問ともいえます。

できるようになるために、たくさん練習するのはもちろんですが、その前に「どのように解いたらいいのか」の道筋（ルート）を知ることが肝心です。

ルートはぜんぶで３つ。

①図を分ける→式を書き出し、\(n\) との関係を見出す

②表をかく→公式を使って式をつくる

③表をかく→つじつまを合わせて式をつくる

以下、くわしく解説していきます。

 

つまずく原因

• 規則性が見つからない
• \(n\) を使って表すことができない

文字式の規則性問題でつまずく原因は、このどちらかです。

このうち「規則性が見つからない」場合の解決策は２つあります。

1. 図を分けて考える
2. 表をかく

 

また、規則性は見つかったけどそのあと「\(n\) を使って式を表すことができない」場合、解決策は３つあります。

1. ひとつひとつ式を書き出して、\(n\) との関係を見出す
2. 公式にあてはめる
3. つじつまを合わせる

 

以上の解決策を組み合わせると、規則性問題を解く方法はおおきくわけて以下の３つになります。

 

これらの方法のうち、応用範囲のいちばん広いのは①です。

まぁだから学校ではこの方法で教えるわけです。

逆に②と③は、応用できない問題もたまにあるけど、コツさえつかめば超簡単に解ける方法です。

よってまずは方法①を、それでダメなら②または③を試してください。

おそらく、学力上位者ほど方法①がしっくりくるはずです。

逆に「数学は苦手」という生徒には②や③がいいでしょう。

 

では、それぞれの方法の中身を具体的に見ていきましょう。

 

 

方法①…学校の教え方

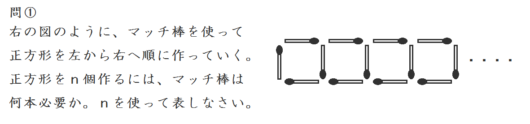
１．図を分けて考えて、規則性をみつける

マッチ棒が何本ずつ増えているかを、図を分けて考える。

以下のように分けると、「３本ずつ増えている」とわかる。

 

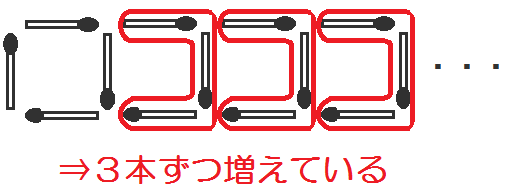
２．ひとつひとつ式を書き出す

規則性をもとに、ひとつずつ、マッチ棒の本数を求める式を立ててみる。

はじめの４本に、３本が追加されていくから、以下のような式になる。

 

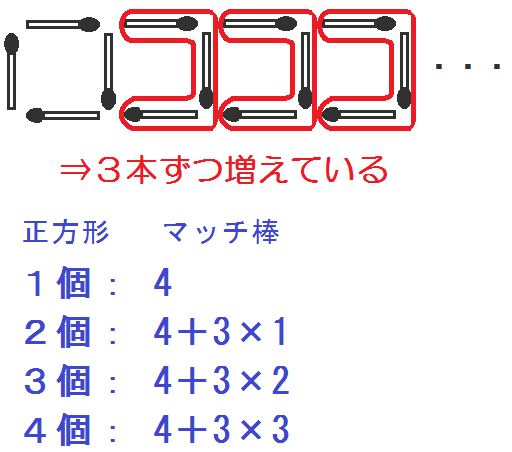
３．変化する数と \(n\) との関係を見出す

式中の変化する数に注目する。

正方形が３個のとき、変化する数は２。

正方形が４個のとき、変化する数は３。

じゃあ正方形が \(n\) 個のとき、変化する数は…\(n-1\) ！

 

４．\(n\) 個目の式を表す

よって \(4+3 \times (n-1) \) と式が立つ。

あとは計算して、おしまい。

答えは \(3n+1\) (本)。

 

 

方法②…裏ワザその１

１．表をかいて、規則性をみつける

上段に正方形(個)、下段にマッチ棒(本)として、表をかいていく。

マッチ棒の本数は実際に数えたらいい。

４つくらい書けば、「３本ずつ増えている」という規則性がみつかるはず。

 

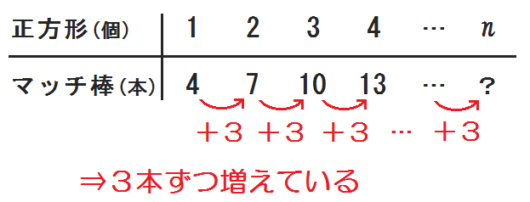
２．\(n\) 個目のマッチ棒の本数は…

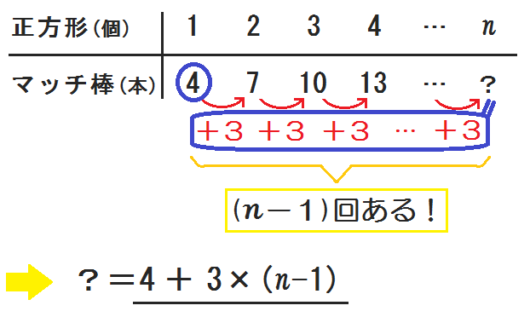
はじめの本数「\(4\)」と、増えている数「\(+3 \ +3 \ +3 \ldots +3\)」に注目。

\(n\) 個目のマッチ棒の本数は、

$$4+(3+3+3+ \ldots +3)$$

で求めることができる。

 

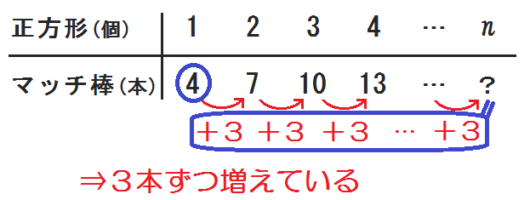
３．増えている数は \( (n-1) \) 回ある

\(+3\) は何回あるか？

正方形３(個)のとき \(+3\) は２回。

正方形４(個)のとき \(+3\) は３回。

じゃあ正方形 \(n\) (個)のとき… \(+3\) は \( (n-1) \) 回！

 

４．\(n\) 個目の式を表す

よって \(4+3 \times (n-1) \) と式が立つ。

あとは計算して、おしまい。

答えは \(3n+1\) (本)。

 

５．公式の紹介

以上のことから、以下の公式が成り立つ。

次からは、この公式を使って解いてもいい。

 

 

方法③…裏ワザその２

１．表をかいて、規則性をみつける

上段に正方形(個)、下段にマッチ棒(本)として、表をかいていく。

マッチ棒の本数は実際に数えたらいい。

４つくらい書けば、「３本ずつ増えている」という規則性がみつかるはず。

（ここまでは方法②と同じ）

 

２．\(3n +\) ■という形は決まり

増えている数が「\(3\)」の時点で、\(3n +\) ■ という形は決まり。

あとは■に入る数字を探すだけ。

 

３．つじつまを合わせる

どこでもいいが、表のいちばん最初に注目しよう。

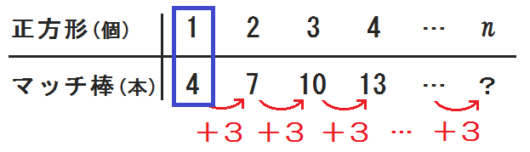
正方形が \(1\) のとき、マッチ棒は \(4\) 。

そこでこんな式がつくれる。

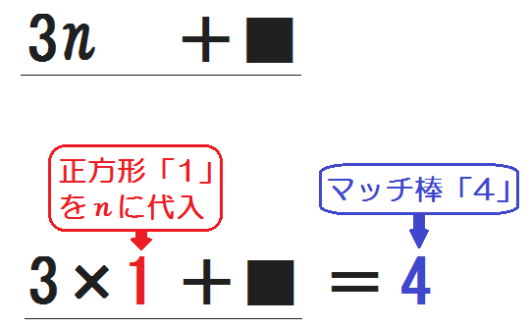
あとは、このつじつまを合わせるために、■に入る数字を考える。

 

４．式を表す

■に入る数字は「\(1\)」。

よって答えは \(3n+1\) (本)。

 

 

注意点

以上３つの方法を紹介しました。

どの方法を使っても、規則性の問題はほぼ解くことができます。

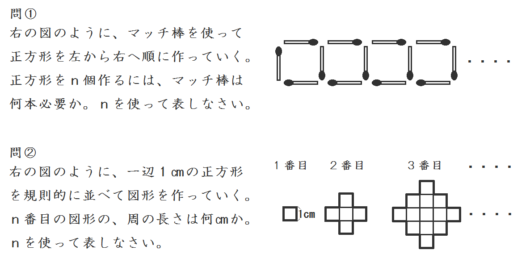
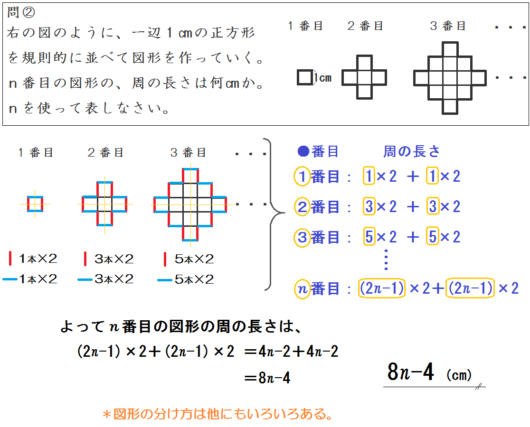
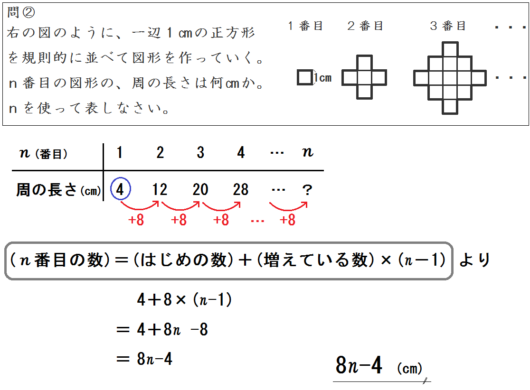
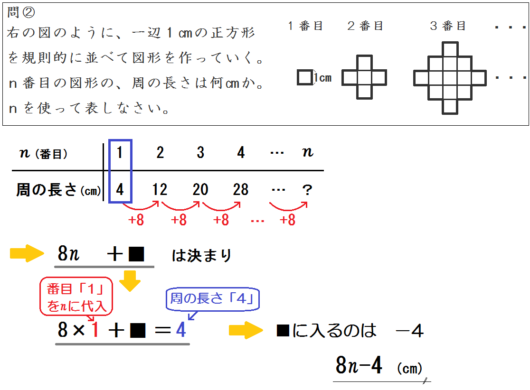
ためしにどれかで、問②をやってみるといいでしょう。

解答および解法は、以下のとおりです。

 

 

 

 

なお、方法②における公式

これは高校２年生以上ならお気づきのとおり、等差数列の一般項を求める公式です。

実は中１「文字と式」の規則性問題は、数学Ｂ「数列」の準備段階でもあるんです。

 

ただ、数列が等差数列だけではないように、規則性問題の中でもこの公式を使えないものがたまに出てきます。

そこで最後に、そんな例外的な問題の解き方・教え方も紹介します。

 

 

例外的な問題

先に結論を言うと、このような問題では方法②および方法③は使えません。

よって方法①に頼ることなります。

つまり図を分けて規則性をみつけ、変化する数と \(n\) との関係をがんばって見出すのです。

ただ問題によっては、「２乗が関係している」と気づきさえすれば、すぐに \(n\) を使った式で表せることもあります。

 

「２乗がある」とすぐわかる問題

この問題を、方法②または方法③で解こうとしてみましょう。

すると、表は下のようになります。

 

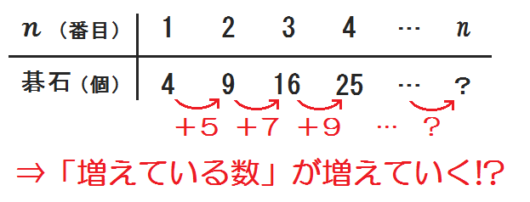
このように、「増えている数」が一定になりません。

この時点で、方法②も方法③も使えないというのがわかります。

では、どうすればいいか？

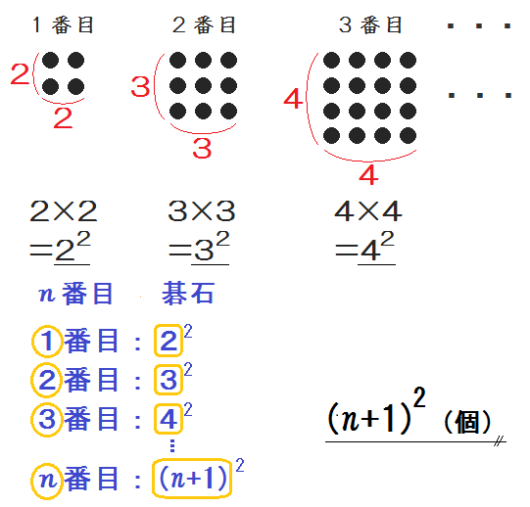
ここで立ち止まって、碁石の数をじっくり眺めてください。

何かに気づきませんか。

そう、すべて２乗した数になっているのです。

 

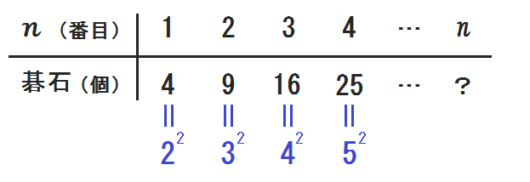
あとは変化する数と \(n\) との関係を考えます。

\(n\) が \(1\) のとき、\(2^2\) 。

\(n\) が \(2\) のとき、\(3^2\) 。

\(n\) が \(3\) のとき、\(4^2\) 。

じゃあ \(n\) のときは…、\( (n+1)^2 \) ！

 

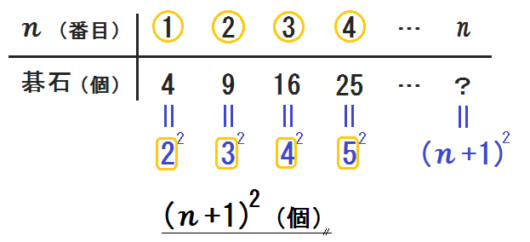
このように、２乗した数が出てきたら、\(n\) を使った式で表すのは難しくありません。

表をかいて、増えている数が一定じゃないときは、\(1,4,9,16,25,36,49 \ldots \) などの数が出てきてないか注意するといいでしょう。

 

 

そうじゃない問題

最後にこの問④を解いてみましょう。

これも方法②または方法③でいこうとして表をかくと、以下のようになります。

 

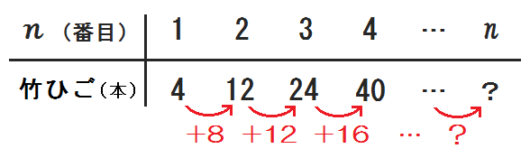
この問題もやはり、「増えている数」が一定になりません。

そして、\(1,4,9,16,\ldots \) といった２乗の数さえ出てこないのです。

こうなったら、方法①で解くしかありません。

つまり図を分けて規則性を見つけ、変化する数と \(n\) との関係を見出して式をつくるのです。

解答例は、以下のようになります。

 

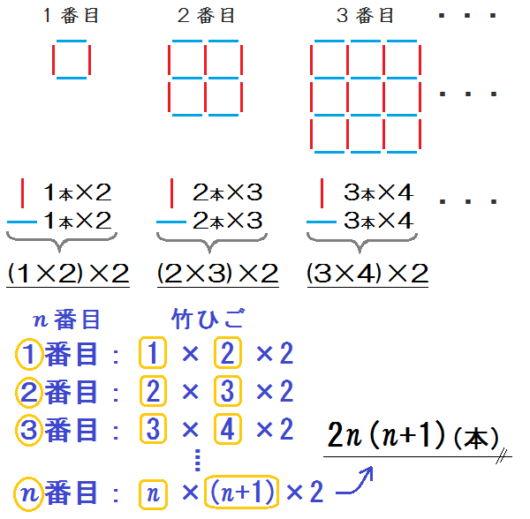
こんな問題も、ごくたまに出てくることがあります。

なお、先に挙げた問③も、この方法①で解くと以下のとおりです。

 

方法①がいちばん応用範囲が広いというのは、こういうわけです。

だから最初にも言いましたが、規則性問題を解く際には、まず方法①（図を分けて規則性をみつける→変化する数と \(n\) との関係を見出す）を使おうとすること。

裏ワザ的な方法②（表をかいて規則性をみつける→公式を使って式を表す）や方法③（表をかいて規則性をみつける→つじつまを合わせて式を表す）は、まだ規則性問題に慣れないけど定期テストが迫っててヤバイ！ってときなどに使うこと。

あまり方法②や③ばかりに頼っていると、使える問題が８割程度に限られてしまいます。

とくに難関校への受験を考えている中学生は、方法①でできるかぎり押し通すべきでしょう。

生徒の状況に応じて、どの方法を薦めるかお考えください。

 

まとめ

規則性問題を解く方法は３つ。

【方法①…学校の教え方】

1. 図を分けて考えて、規則性を見つける。
2. ひとつひとつ式を書き出し、変化する数と \(n\) との関係を見出す。
3. \(n\) を使った式で表す。

 

【方法②…裏ワザその１】

1. 表を書いて、規則性を見つける。
2. 公式「（ \(n\) 番目の数）＝（はじめの数）＋（増えている数）×（ \(n-1\) ）」に当てはめる。
3. \(n\) を使った式で表す。

 

【方法③…裏ワザその２】

1. 表を書いて、規則性を見つける。
2. つじつまを合わせて、「●\(n\) ＋■」の■に当てはまる数を探す。
3. \(n\) を使った式で表す。

 

ただし、方法②、③が使えない問題もたまにある。

表を書いて、２乗した数が出てきたら、\(n\) を使って表すだけ。

２乗した数も出てこない場合は、方法①で解くしかない。

 

 

以上、中学１年数学「文字と式」における規則性の問題でした。

次回からは中１数学「一次方程式」の指導法について解説していく予定です。

NEXT→中１「１次方程式」でつまずく原因と解決法①　導入

（数学指導法の記事一覧はまとめページへ）