中学数学「平方根」のコツ① 平方根とは／平方根の大小

中学数学のつまずき解消をめざすこの連載。

今回から中３「平方根」に入ります。

１回目は平方根とは何か、そして平方根の大小問題をあつかいます。

ここで中学生がつまずく点はおもに３つ。

• 平方根とは何か、ちゃんと理解しないまま授業がすすんじゃった
• 「平方根を求めよ」と「根号を使わないで表せ」の区別ができない
• 大小問題の応用になるとできなくなる

つまり、

• 「平方根とは何か、ひとことで説明せよ」
• 「\(49\) の平方根を求めよ」「\(\sqrt{49}\) を根号を使わないで表せ」
• 「\(1.5 \lt \sqrt{n} \lt 2.8\) にあてはまる自然数 \(n\) をすべて求めよ」

などの問題でつまずくのです。

そこでこの記事では、上の３点をわかりやすく、かつ深く、解説します。

（たとえば \(\sqrt{2}\) という数が出てきた歴史的経緯も紹介します）

いつもジュウゴが使っている教え方です。

ここで紹介するコツを、中学生のみならず、指導者や保護者の方もぜひ参考にしてください。

平方根とは何か

まず平方根とは何かの理解から。

平方根とはつまり、二乗のもとのことです。

二乗（平方）のもと（根）

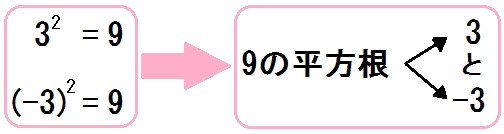
たとえば、\(3^2\) は \(9\) です。

よって、\(9\) の二乗のもとは、\(3\) 。

ただ、二乗して \(9\) になる数は他にもある。

そう、\(-3\) 。\((-3)^2 =9\) だからね。

よって、\(9\) の二乗のもとをぜんぶ答えろと言われたら？
→ \(3\) と \(-3\) 。

このように、平方根とは「二乗のもと」のこと。

じゃ、\(36\) の平方根は？
→ \(6\) と \(-6\) 。

じゃ、\(49\) の平方根は？
→ \(7\) と \(-7\) 。

かんたんだね。

ちなみに、「\(3\) と \(-3\)」って書くのがめんどうな場合、「\(\pm 3\)」と書く。
「プラスマイナス３」と読みます。
これで「\(+3\) と \(-3\)」を同時に表したことになります。

だから、

\(36\) の平方根は \(\pm 6\)
\(49\) の平方根は \(\pm 7\)

と答えてもOK。

 

分数や小数の平方根

じゃ、\(\frac{9}{49}\) の平方根はいくらだろう？

これ、分子・分母それぞれの二乗のもとを考えればいいね。

答えは \(\pm \frac{3}{7}\) 。

同じように、

\(\frac{4}{25}\) の平方根は \(\pm \frac{2}{5}\)
\(\frac{1}{81}\) の平方根は \(\pm \frac{1}{9}\) 。

 

じゃ、\(0.04\) の平方根はいくらだろう？

二乗して \(0.04\) になる数を考えればいいね。

答えは \(\pm 0.2\) 。

\( 0.2 \times 0.2 = 0.04\) だからね。

同じように、

\(0.16\) の平方根は \(\pm 0.4\)
\(0.01\) の平方根は \(\pm 0.1\) 。

 

二乗した数をおぼえてしまおう！

じゃ、\(289\) の平方根は？
→ \(\pm 17\) 。

\(\frac{121}{196}\) の平方根は？
→ \(\pm \frac{11}{14}\) 。

\(1.69\) の平方根は？
→ \(\pm 1.3\) 。

こんな問題も、平方根単元ではたまに出てくる。

だから、中３生は、\(10\) ～ \(20\) の二乗した数もおぼえてしまうといい。

以下の数を３分でおぼえて。

• \(100 = 10^2\)
• \(121 = 11^2\)
• \(144 = 12^2\)
• \(169 = 13^2\)
• \(196 = 14^2\)
• \(225 = 15^2\)
• \(256 = 16^2\)
• \(289 = 17^2\)
• \(324 = 18^2\)
• \(361 = 19^2\)
• \(400 = 20^2\)

これらをぜんぶおぼえたら、他の生徒と差をつけられるよ！

 

練習問題

では、ここまでの知識を確認しよう。

以下の練習問題をどうぞ。

問１）次の数の平方根を求めよ。

① \(64\) 　　② \(144\) 　　③ \(0\)

④ \(\frac{25}{36}\) 　　⑤ \(\frac{1}{324}\) 　　⑥ \(\frac{256}{225}\)

⑦ \(0.09\) 　　⑧ \(3.61\) 　　⑨ \(0.0169\)

答.①\(\pm 8\)  ②\(\pm 12\)  ③\(0\)  ④\(\pm \frac{5}{6}\)  ⑤\(\pm \frac{1}{18}\)  ⑥\(\pm \frac{16}{15}\)  ⑦\(\pm 0.3\)  ⑧\(\pm 1.9\)  ⑨\(\pm 0.13\)

ルート（ √ ）の導入

次にルート（根号、\(\sqrt{\quad}\)）を説明します。

ルートとは、どうしても二乗のもとが見つからない数について、苦しまぎれに人類がつけた記号のことです。

２の平方根

たとえば、二乗して \(2\) になる数。

つまり２の平方根は、過去の数学者たちが必死に探してもついに見つかりませんでした。

たとえば古代インドでは

$$ \frac{577}{408} \ ( \mbox{≒ 1.4132156862745…} ) $$

を２の平方根とした数学者もいました。

でもこれ、二乗してもキッチリ２にはなりません。

$$ \left( \frac{577}{408} \right)^2 = 2.0000060073048\mbox{…} $$

それどころか、２の平方根は分数や小数では表せないということがわかったのです。

ここで数学者たちは考えます。

いまある数では、２の平方根は表せない…。
でも「２の平方根はありません」じゃ満足できない。
そうだ！新しい数をつくったらいいんだ！
分数や小数ともちがう、新たな数を！

こうして数学者たちは、「２の平方根は \(\pm \sqrt{2}\) とする」と決めたのです。

だからルートとは、二乗のもとがない・つまり平方根が分数や小数でも表せない数にたいして、「この記号をつけたら２の平方根ってことにする！じっさいはなんだかわからないけど、とにかくそう決めたの！」としたものなんです。

 

４の平方根

よって、３の平方根は \(\pm \sqrt{3}\) です。

５の平方根は \(\pm \sqrt{5}\) 、６の平方根は \(\pm \sqrt{6}\) です。

こう表すしか、方法がないからです。

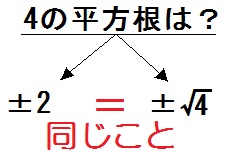
ではここで、４の平方根は何か考えてみましょう。

うん、\(\pm 2\) ですね。

ただもし、二乗して４になる数が思いつかなかったらどう書きますか？

そう、\(\pm \sqrt{4}\) ですね。

つまり \(\pm 2\) と \(\pm \sqrt{4}\) は同じ数のことを言ってるんです。

分けて書くならこんなかんじ。

$$ 2 = \sqrt{4} \ , \ -2 = – \sqrt{4} $$

同じりくつで、９の平方根は \(\pm 3\) だし \(\pm \sqrt{9}\) でもある。

だから

$$ 3 = \sqrt{9} \ , \ -3 = – \sqrt{9} $$

同じりくつで、121の平方根は \(\pm 11\) だし \(\pm \sqrt{121}\) でもある。

だから

$$ 11 = \sqrt{121} \ , \ -11 = – \sqrt{121} $$

以上の式を左右逆に書けば、

\begin{eqnarray} \sqrt{4} &=& 2 \ , \ – \sqrt{4} = -2 \\ \sqrt{9} &=& 3 \ , \ – \sqrt{9} = -3 \\ \sqrt{121} &=& 11 \ , \ – \sqrt{121} = -11 \end{eqnarray}

となります。

ここから「ルートを使わないで表せ」という問題が出てくるんです。

「ルートを使わないで表せ」

次の数を、√を使わないで表してみてください。

1. \(\sqrt{49}\)
2. \(- \sqrt{100}\)
3. \(\sqrt{\frac{25}{64}}\)
4. \(- \sqrt{0.36}\)

答えは以下のとおり。

1. \(\sqrt{49} = 7 \)
2. \(- \sqrt{100} = -10 \)
3. \(\sqrt{\frac{25}{64}} = \frac{5}{8}\)
4. \(- \sqrt{0.36} = -0.6 \)

ここまでくれば、

「\(49\) の平方根を求めよ」→ \(\pm 7\)

「\(\sqrt{49}\) を√を使わないで表せ」＝ \(7\)

この違いがわかりましたね。

ちなみにテストのときは、\(49= \pm 7\) と書かないように注意しましょう。

\( \pm 7\) は \(49\) の平方根であって、等しいものじゃないからです。

気をつけて。

 

練習問題

では、ルートの知識も練習問題をやって確認しましょう。

質問はコメント欄からどうぞ。

問２）次の数の平方根を求めよ。

① \(7\)   ② \(\frac{3}{2}\)   ③ \(0.4\)

問３）次の数を、√を使わないで表せ。

① \(-\sqrt{289}\)   ② \(- \sqrt{\frac{9}{100}}\)   ③ \( \sqrt{3.24}\)

答. 問２①\(\pm \sqrt{7}\)  ②\(\pm \sqrt{\frac{3}{2}}\)  ③\(\pm \sqrt{0.4}\)
問３①\(-17\)  ②\(- \frac{3}{10}\)  ③\(1.8\)

平方根の大小

さいごに、平方根の大小問題を説明します。

平方根の大小問題のコツは、ぜんぶ√にしてルートの中身をくらべるだけ。

√ の中身をくらべる

例題１）次の各組の数の大小を、不等号を使って表せ。

1. \(\sqrt{13} \ , \ \sqrt{11}\)
2. \(- \sqrt{5} \ , \ – \sqrt{4}\)

この例題１は、出てくる数ぜんぶ、ルートがついてます。

よってルートの中身の大小をくらべるだけ。

答えは

1. \(\sqrt{13} \gt \sqrt{11}\)
2. \(- \sqrt{5} \lt – \sqrt{4}\)

となります。

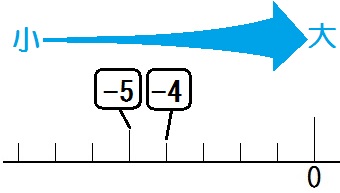
ちなみに2.は \(-5 \lt -4\) だから、こう。

マイナスが付いてたら大小関係に注意しましょう。数直線の右にあるほど大きい数だよ。

 

ムリヤリ √ にする

例題２）次の各組の数の大小を、不等号を使って表せ。

1. \(\sqrt{15} \ , \ 4 \)
2. \(0.3 \ , \ \sqrt{0.3}\)

この例題２には、ルートのない数があります。

こんな場合は、\(4 = \sqrt{16}\) とする。

つまりムリヤリ√にして中身の大小をくらべるんです。

\(\sqrt{16} = 4\) だから、逆に \(4 = \sqrt{16}\) ともできるもんね。

よって答えは、

1. \(4 = \sqrt{16}\) より
   \(\sqrt{15} \lt \sqrt{16}\)
   よって \(\sqrt{15} \lt 4 \)
2. \(0.3 = \sqrt{0.09}\) より
   \(\sqrt{0.09} \lt \sqrt{0.3}\)
   よって \(0.3 \lt \sqrt{0.3}\)

ルートのある数とない数の大小はこうやってくらべましょう。

 

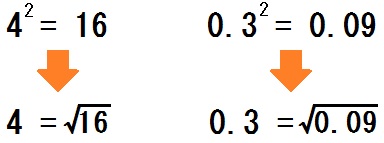
応用問題の解き方 その１

例題３）\(1.5 \lt \sqrt{n} \lt 2.8\) にあてはまる自然数 \(n\) をすべて求めよ。

ここまでくれば、この応用問題もできますね。

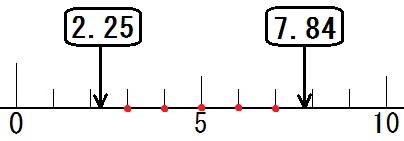
\(1.5 = \sqrt{2.25}\) , \(2.8 = \sqrt{7.84}\) だから、与式は

$$ \sqrt{2.25} \lt \sqrt{n} \lt \sqrt{7.84} $$

あとはルートの中身をくらべるだけ。

2.25より大きくて、7.84より小さい自然数ってなに？

答. \(n= 3 , 4 , 5 , 6 , 7\)

となります。

不安な人は、自分で数直線を書いてひとつひとつ確かめるといいでしょう。

 

応用問題の解き方 その２

例題３）\(1.5 \lt \sqrt{n} \lt 2.8\) にあてはまる自然数 \(n\) をすべて求めよ。

で、平方根の大小問題にはもうひとつの解き方があります。

それは、ぜんぶ二乗しちゃう方法。

\( 1.5^2 = 2.25\) , \( 2.8^2 = 7.84\) 。

また \( ( \sqrt{n} )^2 = n\) です。

だってルートって二乗のもとのことだからね。

すると与式から

$$ 2.25 \lt n \lt 7.84 $$

これに当てはまる自然数nをぜんぶ書く。

答. \(n= 3 , 4 , 5 , 6 , 7\)

となります。

じつは例題２もこの「ぜんぶ二乗する方法」でもいける。

1. \( ( \sqrt{15} )^2 = 15\) , \(4^2 =16\) より
   \( \sqrt{15} \lt 4\)
2. \( 0.3^2 = 0.09\) , \( ( \sqrt{0.3} )^2 = 0.3\) より
   \( 0.3 \lt \sqrt{0.3}\)

中学生はこの両方の方法を知っておきましょう。

両方とも使いこなせれば、たとえば以下の練習問題の問６もできるようになります。

以上、平方根の大小問題でした。

 

練習問題

問４）次の各組の数の大小を、不等号を使って表せ。

① \(- \sqrt{10} \ , \ – \sqrt{11}\)   ② \(\sqrt{7} \ , \ 3 \)

③ \(0.8 \ , \ \sqrt{0.8} \)   ④ \(-1.5 \ , \ – \sqrt{2.56}\)

問５）\(1.7 \lt \sqrt{n} \lt 2.5\) にあてはまる自然数 \(n\) をすべて求めよ。

問６）\( \sqrt{3} \lt n \lt \sqrt{26}\) にあてはまる自然数 \(n\) をすべて求めよ。

答. 問４①＞　②＜　③＜　④＞
問５ \(n= 3,4,5,6\)
問６ \(n=2,3,4,5\)

＊問６はちょっと難問です。質問などはコメント欄からどうぞ。

[関連記事]
中１数学「正負の数」②　乗除、累乗

 

まとめ

平方根とは「二乗のもと」。

9の平方根→ \(\pm 3\) のように書く。

10～20の二乗した数もおぼえるとテストで差がつく。

 

ルート（√）とは、二乗のもとが見つからない数にムリヤリつけた記号。

2の平方根→ \(\pm \sqrt{2}\) のように書く。

だから \(\sqrt{2}\) や \(- \sqrt{2}\) は分数や小数とはちがう、新しい数。

このルートを使うと、二乗のもとが見つかる数の平方根は２通りの書き方がある。

たとえば9の平方根は \(\pm \sqrt{9}\) あるいは \(\pm 3\) 。

ここから \(\sqrt{9}=3\) のような問題も出てくる。

 

平方根の大小問題の基本は、√の中身をくらべること。

ルートのない数がある大小問題の場合、

• ムリヤリ√にする
• ぜんぶ二乗してくらべる

という２つの方法がある。

 

以上、平方根とは何か、ルートとは何か、そして平方根の大小問題の解き方でした。

次回は中３数学 平方根単元の２回目。

「無理数・有理数とは何か」「循環小数⇔分数の変換のしかた」を解説します。

NEXT→中学数学「平方根」のコツ② 有理数と無理数／循環小数と分数