連立方程式の文章題、4回目です。
今回は割合の問題。
- 20%の食塩水と12%の食塩水を混ぜて…
- 原価の6割増しの定価をつけて…
- 今年は昨年と比べると男子は8%増え、女子は5%減って…
- 100gあたりの栄養成分の重さは…
こういう4パターンの問題について、それぞれの解き方を解説していきます。
練習問題も載せるので、割合の問題ができるようになりたいというすべての中学生の参考にしてください。
[前の記事]連立方程式 文章題③【道のり問題】
[次の記事]1次関数①【1次関数とは】
割合とは何か

その前にまず、割合とは何かをかんたんに復習しましょう。
割合問題でつまずく大きな原因は、割合の理解があやふやなことにあるからです。
割合とは「ある量が基準に対してどれくらいあるかという数値」。
つまり、何倍かってことです。
たとえば「○割」「○割増し」「○割引き」というのは以下のとおり。
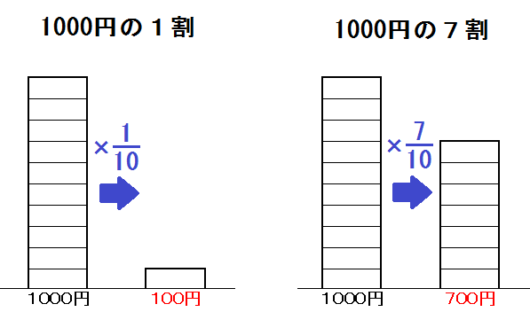
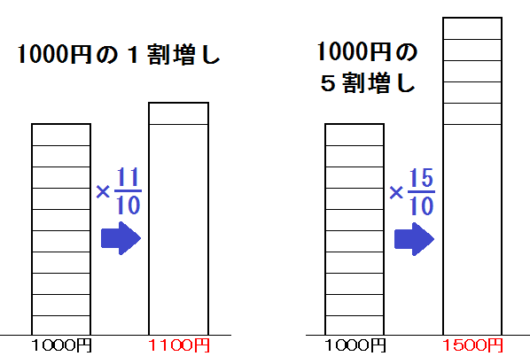
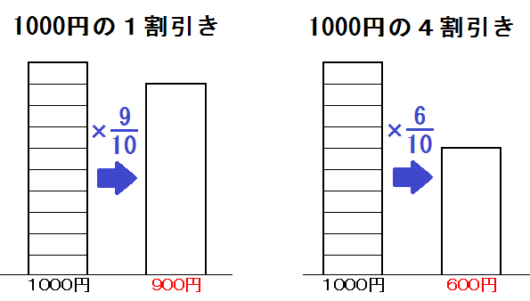
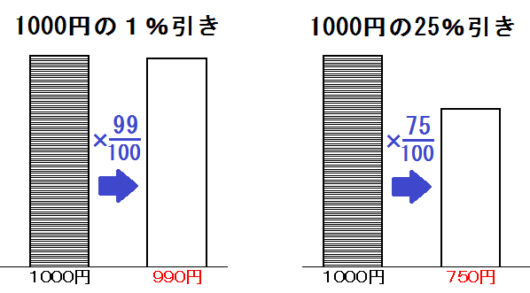
また「○%」「○%増し」「○%引き」というのは以下のとおり。
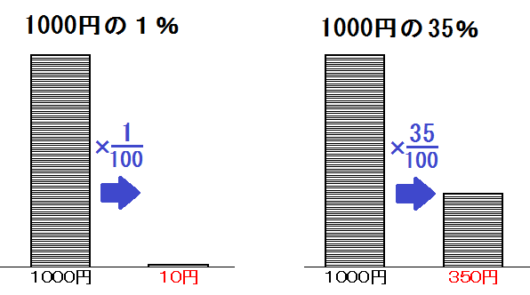
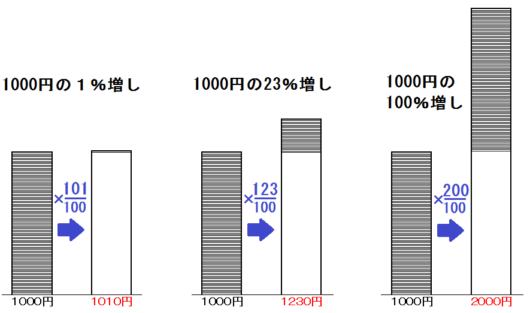
つまり、800円の6割増しだったら \(800 \times \frac{16}{10}\)
90円の10%引きだったら \(90 \times \frac{90}{100}\)
などのように、基準にかけ算すればいいだけ。
よって、文字が入っても以下のように計算できます。
(じゅうぶん理解したい人は以下の表をまるまる書き写してください)
以上が理解できれば、割合問題に入る準備はOKです。
このあたりの詳しいことは、中1の1次方程式文章題ですでに解説済みです。
もっと丁寧に教えてほしいという場合は下のリンクからどうぞ。
食塩水の問題

では、実際の連立方程式文章問題を解いていきましょう。
まず「食塩水の問題」から。
ここでのコツは、計6マスの表を書くことです。
解き方のコツ
例題1)20%の食塩水と12%の食塩水を混ぜて、15%の食塩水を400g作りたい。2種類の食塩水をそれぞれ何g混ぜればよいか。
とりあえず「20%の食塩水を \(x\) g、12%の食塩水を \(y\) g混ぜるとする。」等と書きます。
次に立式していきますが、食塩水の問題でむずかしいのは、どうやって方程式を2つ作ればいいのか整理がつかないこと。
そこで、以下のような表を書きましょう。

つまり上の行には食塩水の重さ、下の行には食塩の重さという、2行×3列の表を余白かなにかに書くんです。
その上には、20%と12%を混ぜて15%を作るんだというような図も描いておきましょう。
そんで、この6マスをぜんぶ埋めていきます。
まずは食塩水の重さから。

これはできますね。
つぎに食塩の重さも埋めましょう。
たとえば「15%の食塩水400g」というのは、この食塩水の中に含まれる食塩の量は400gの15%ですよーという意味です。
400gの15%= \(400 \times \frac{15}{100}\) g
これが、15%の食塩水の中にある食塩の重さです。
同じようにして、20%の食塩水 \(x\) gも、12%の食塩水 \(y\) gも、表せますね。
20%:\(x \times \frac{20}{100}\)
12%:\(y \times \frac{12}{100}\)
つまり、

こうして表をすべて埋めれば、
\begin{eqnarray} \left\{ \begin{array}{l} x+y=400 \\ \frac{20}{100}x + \frac{12}{100}y =400 \times \frac{15}{100} \end{array} \right.\end{eqnarray}
と連立方程式が立ちます。
以上のように、食塩水の問題では、計6マスの表を書いて埋める。
これが立式のコツです。
(例題1の答えは20%の食塩水150g、12%の食塩水250g)
>Amazonプライム・ビデオで「地の塩(大泉洋主演)」を観る
練習問題
食塩水の練習問題を用意しました。
ちょっと応用をきかせてますが、ぜひ解いてみてください。
質問はコメント欄からどうぞ。
問1)4%の食塩水に食塩を加えて、20%の食塩水を960g作る。4%の食塩水と食塩、それぞれ何g用意すればいいか。
答.4%の食塩水800g、食塩160g
定価の問題

次に、「商品の定価の問題」です。
ここは原価、定価などの言葉の意味さえわかっていれば、まったくむずかしくありません。
解き方のコツ
例題2)商品A,Bがあり、Aには原価の6割増しの定価、Bには原価の8割増しの定価がついている。A1個とB2個の定価の合計は2900円で、Aの定価はBの定価より470円高い。A1個とB1個の原価をそれぞれ求めよ。
「A1個の原価を \(x\) 円、B1個の原価を \(y\) 円とする。」
まずはこのセリフ、忘れずに書きましょう。
次に連立方程式を立てますが、いちおう確認します。
- 原価=仕入れ値のこと
- 定価=売る側がつけた値段
です。
このあたり、よくわからなければ下の記事で詳しく解説しています。読んでから戻ってきてください。
まぁ中学生だからまだ商売のことなんてだいたいの理解でOKです。
とにかく、Aの定価は「原価の6割増し」、Bの定価は「原価の8割増し」なので、
Aの定価:\(x \times \frac{16}{10}\)
Bの定価:\(y \times \frac{18}{10}\)
ですね。
あとは文章に沿って立式するだけ。
\begin{eqnarray} \left\{ \begin{array}{l} \frac{16}{10}x + \frac{18}{10}y \times 2 =2900 \\ \frac{16}{10}x = \frac{18}{10}y +470 \end{array} \right.\end{eqnarray}
以上のように、商品の定価の問題では、定価を \(x , y\) で表してから立式するとラクチンです。
(例題2の答えは、Aの原価800円、Bの原価450円)
>Amazonプライム・ビデオで「武士の家計簿(堺雅人主演)」を観る
練習問題
では、商品の定価の練習問題です。
以下の問2は三重県の2019年度公立高校入試問題になります。
連立方程式の文章題は入試でも頻出。
なかでも割合問題は毎年よく出ます。
ぜひチャレンジしてみてください。
問2)ある店で、ノート1冊とボールペン1本を定価で買うと、合計の値段は145円になる。ノートが定価の10%引き、ボールペンが低下の20%引きとなる割引セールで、ノート2冊とボールペン3本を買うと、合計の値段は294円となった。ノート1冊とボールペン1本の定価をそれぞれ求めよ。(2019年度三重県公立高校入試問題)
答.ノート90円、ボールペン55円
増減の問題

つづいて3パターン目は「増減の問題」を解説します。
ここでの重要なコツは、昔のほうを \(x , y\) とすることです。
解き方のコツ
例題3)ある中学校の昨年の生徒数は420人だった。今年は昨年と比べると、男子は8%増え、女子は5%減って、全体としては5人増えた。今年の男子、女子の生徒数をそれぞれ求めよ。
この例題3、「今年の男子を \(x\) 人、今年の女子を \(y\) 人とする」としてはいけません。
なぜなら、時間経過によって何かの量が増減する場合、基準はつねに昔のほうにあるからです。
昔の8%増、昔の5%減なんです。
よって一行目は「昨年の男子を \(x\) 人、昨年の女子を \(y\) 人とする。」と書きます。
このあたりの詳しい話も過去記事を見てください。
ただ、増減の問題、連立方程式をつくるのはカンタンです。
\begin{eqnarray} \left\{ \begin{array}{l} x+y=420 \\ \frac{108}{100}x + \frac{95}{100}y = 420+5 \end{array} \right.\end{eqnarray}
今年の男子の生徒数は、\(x\) 人の8%増だから
$$ x \times \left( 1+ \frac{8}{100} \right) $$
今年の女子の生徒数は、\(y\) 人の5%減だから
$$ y \times \left( 1- \frac{5}{100} \right) $$
ですもんね。
あるいは、2つめの方程式は増減だけに注目してつくってもいいです。
\begin{eqnarray} \left\{ \begin{array}{l} x+y=420 \\ \frac{8}{100}x – \frac{5}{100}y = 5 \end{array} \right.\end{eqnarray}
女子は5%減っているので、\(-\frac{5}{100}y\) と、マイナスであることに注意してください。
そこだけ注意すれば、計算はこっちのほうがカンタンです。
以上のように、増減の問題では、昔のほうを \(x , y\) とする。
このコツを使って解いていってください。
(例題3の答えは男子216人、女子209人)
>Amazonプライム・ビデオで「まんが日本昔ばなし」を観る
練習問題
ちなみに例題3を最後まで解くと以下のようになります。
2つめの連立方程式を使いますね。
\begin{eqnarray} \left\{ \begin{array}{l} x+y=420 \ \large{\mbox{…①}} \\ \frac{8}{100}x – \frac{5}{100}y = 5 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}
②より
$$ 8x -5y = 500 \ \large{\mbox{…②’}}$$
①より
$$ 5x +5y = 2100 \ \large{\mbox{…①’}}$$
②’+①’をして
\begin{eqnarray} 13x &=& 2600 \\ x &=& 200 \ \large{\mbox{…③}} \end{eqnarray}
③を①に代入して
\begin{eqnarray} 200+y &=& 420 \\ y &=& 220 \end{eqnarray}
よって今年の男子は \(\frac{108}{100} \times 200 = 216\)
また、今年の女子は \(\frac{95}{100} \times 220 = 209\)
答.男子216人、女子209人
最後の計算を忘れないように。
\(x , y\) は昨年の男女の生徒数です。注意しましょう。
では、増減の練習問題をどうぞ。
質問はコメント欄から。
問3)ある工場の従業員数は、昨年度は1200人だったが、今年度は男子が3%減少し、女子が9%増加し、全体で6%増加した。今年度の男子、女子の従業員数をそれぞれ求めよ。
答.男子291人、女子981人
食品の成分の問題
最後に、「食品の栄養成分の問題」です。
割合の問題そのものというわけでもないんですが、割合と似たような考え方で解くので、ここで取り上げます。
なにより、高校入試でよく出ます。
解き方のコツ
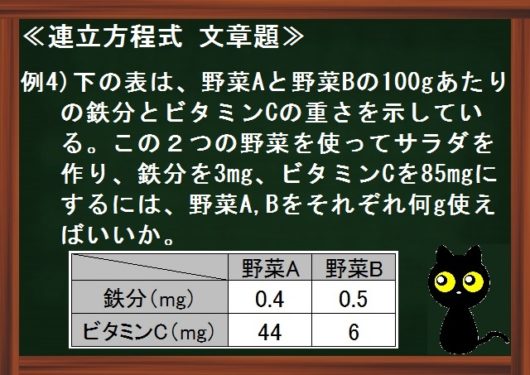
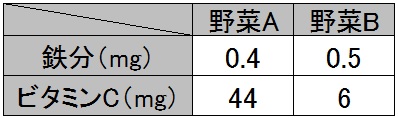
例題4)右の表は、野菜Aと野菜Bの100gあたりの鉄分とビタミンCの重さを示している。
この2つの野菜を使ってサラダを作り、鉄分を3mg、ビタミンCを85mgにするには、野菜A,Bをそれぞれ何g使えばいいか。
とりあえず、野菜Aと野菜Bをそれぞれ何g使えばいいかというのが求める量なので、「野菜Aを \(x\) g、野菜Bを \(y\) gとする。」と書きます。
さて、いきなり立式がむずかしい場合は、まず具体例で考えてみましょう。
たとえば野菜Aを \(750\) g使ったとき、鉄分はどれだけ含まれるでしょうか?
いま100gあたりの鉄分が0.4mgです。じゃ、1gあたりの鉄分は?
\(\frac{0.4}{100}\) mgですね。100で割ればいいもんね。(分数のなかに小数がありますがとりあえず置いとく)
んじゃ、750gあたりの鉄分はというと、
$$ \frac{0.4}{100} \times 750 $$
で求めることができます。
同じように、野菜Aを \(750\) g使ったとき、ビタミンCはどれだけ含まれるか?
$$ \frac{44}{100} \times 750 $$
で求めることができます。
このように、まず1gあたりの栄養成分の量を出して、それを食品の重さだけ掛け算すれば、その食品に含まれる栄養成分はどれだけあるかが求まります。
栄養成分表示の例
(CGCホームページより)
じゃ、野菜Aを \(x\) g、野菜Bを \(y\) g使ったとき、含まれる鉄分はそれぞれ
$$ \mbox{野菜A…} \frac{0.4}{100}x \quad \mbox{野菜B…} \frac{0.5}{100}y $$
また、ビタミンCはそれぞれ
$$ \mbox{野菜A…} \frac{44}{100}x \quad \mbox{野菜B…} \frac{6}{100}y $$
と表せますね。
んで、鉄分の合計が3mg、ビタミンCの合計が85mgなんです。
連立方程式は下のとおりです。
\begin{eqnarray} \left\{ \begin{array}{l} \frac{0.4}{100}x + \frac{0.5}{100}y =3 \\ \frac{44}{100}x + \frac{6}{100}y =85 \end{array} \right.\end{eqnarray}
以上のように、食品の栄養成分の問題では、まず1gあたりの栄養成分の量を出してそれを食品の重さでかける。
これが解くときのコツになります。
(例題4の答えは野菜A125g、野菜B500g)
練習問題
では、最後の練習問題です。
以下の問4も昨年度の公立高校入試問題(山口県)。
ぜひチャレンジしてみてください。
質問はコメント欄からどうぞ。
問4)Sさんは、豆腐と牛ひき肉を混ぜて豆腐ハンバーグを作ることにした。表1、表2は、Sさんが、豆腐40gあたりと牛ひき肉100gあたりの栄養成分を調べ、まとめたものである。
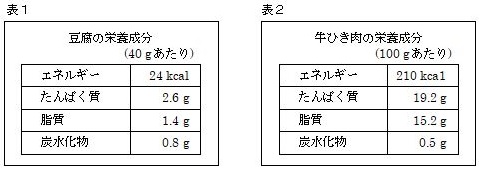
(1)表1をもとに、豆腐100gあたりの脂質の重さを求めなさい。
(2)表1、表2をもとに、豆腐と牛ひき肉を、重さの合計が120gで、エネルギーの総和が150kcalとなるように用意する。用意する豆腐の重さを \(x\) g、牛ひき肉の重さを \(y\) gとして連立方程式をつくり、豆腐、牛ひき肉の重さをそれぞれ求めなさい。
(2019年度山口県公立高校入試問題)
答.(1)3.5g (2)豆腐68g、牛ひき肉52g
まとめ

連立方程式 文章題における「割合の問題」。
まとめます。
○割合とは、ある量が基準に対してどれくらいあるかという数値。ようするに、何倍かってこと。

○食塩水の問題のコツは、計6マスの表を書いて埋めること。
○商品の定価の問題は、定価を \(x , y\) で表してから立式するとラクチン。
○増減の問題のコツは、昔のほうを \(x , y\) とすること。
○食品の栄養成分の問題は、まず1gあたりの栄養成分の量を出してそれを食品の重さでかけること。

*1次方程式の割合問題はこちら
これにて中2連立方程式の解説は終わりです。
おつかれさまでした。
次回からは1次関数を解説していく予定です。
→
≪連立方程式の記事一覧≫







コメント
本当にわかりやすく、素晴らしいサイトですね。
中学数学、一次関数以降も載せてくださるとありがたいです。
ぜひよろしくお願いします!
すみません計算ミスでした。
有難うございました‼️
問1の食塩水の問題の解法をお願いします。
X+y=960
4/100×x+y=192 の連立方程式を立てたのですが、答えが合いません。よろしくお願いします!
食品の連立方程式、解けました。いい問題を有難うございました‼️
食品の連立方程式の、練習。豆腐ハンバーグの問題の解き方をおしえてください。豆腐X+ひき肉y=150は立つたのですが、あとの式が答えが合いません。よろしくお願いします。
いつも参考にさせていただいております、どうもありがとうございます。
中2数学「1次関数」もぜお願いします!