中3「平方根」の5回目、近似値の問題につづいて、「式の値を求めよ」という問題を解説します。
式の値の問題

このような式の値の問題。
解き方のコツは、因数分解や展開をしてから代入すること。
以下、具体的に見ていきましょう。
\(x^2 +2xy-3y^2\) の値
例題2) \(x=6+ \sqrt{6}\) , \(y=6- \sqrt{6}\) のとき、次の式の値を求めよ。
①\(x^2 +2xy-3y^2\)
①の式にいきなり \(x=6+ \sqrt{6}\) , \(y=6- \sqrt{6}\) を代入してもいいんですが、計算がたいへんそう。
そこで、①を因数分解してから代入します。
解答例はこのとおり。
\begin{eqnarray} \mbox{例2)①} & & x^2 +2xy-3y^2 \\ &=& (x-y)(x+3y) \\ & & x=6+ \sqrt{6} \ , \ y=6- \sqrt{6} \ \mbox{を代入して} \\ & & \{ (6+ \sqrt{6})-(6- \sqrt{6} ) \} \{ (6+ \sqrt{6})+3(6- \sqrt{6} ) \} \\ &=& (6+ \sqrt{6} -6+ \sqrt{6} ) (6+ \sqrt{6} +18 -3 \sqrt{6} ) \\ &=& 2 \sqrt{6} (24-2 \sqrt{6} ) \\ &=& 48 \sqrt{6} -24 \end{eqnarray}
ここで注意すべきは、\(x , y\) の値を代入したあとの
$$ \{ (6+ \sqrt{6})-(6- \sqrt{6} ) \} \{ (6+ \sqrt{6})+3(6- \sqrt{6} ) \} $$
という式をきちんと書くこと。
代入とかっこ外しを同時にやろうとすると、高確率で計算ミスします。
また、「因数分解がパッと思いつかない」という生徒は以下の記事を復習してください。

\((2x+y)^2 -(x+2y)^2\) の値
例題2) \(x=6+ \sqrt{6}\) , \(y=6- \sqrt{6}\) のとき、次の式の値を求めよ。
②\((2x+y)^2 -(x+2y)^2\)
②も同様にやってみましょう。
\begin{eqnarray} \mbox{例2)②} & & (2x+y)^2 -(x+2y)^2 \\ &=& 4x^2 +4xy+y^2 -(x^2 +4xy+4y^2 ) \\ &=& 4x^2 +4xy+y^2 -x^2 -4xy-4y^2 \\ &=& 3x^2 -3y^2 \\ &=& 3(x^2 -y^2) \\ &=& 3(x+y)(x-y) \\ & & x=6+ \sqrt{6} \ , \ y=6- \sqrt{6} \ \mbox{を代入して} \\ & & 3 \{ (6+ \sqrt{6})+(6- \sqrt{6} ) \} \{ (6+ \sqrt{6})-(6- \sqrt{6} ) \} \\ &=& 3(6+ \sqrt{6} +6- \sqrt{6} ) (6+ \sqrt{6} -6+ \sqrt{6} ) \\ &=& 3 \times 12 \times 2 \sqrt{6} \\ &=& 72 \sqrt{6} \end{eqnarray}
こうした式の値の解き方は、じつは中3「多項式」⑥の記事で解説しました。
そして、例題3のやり方もすでに解説しています。
\(x^2 +y^2\) の値
例題3) \(x+y= \sqrt{7}\) , \(xy=3\) のとき、\(x^2 +y^2\) の値を求めよ。
この問題、式がそのままでは代入できません。
そこで、以下の式変形を使うんでしたね。
\begin{eqnarray} & & x^2 +y^2 \\ &=& (x+y)^2 -2xy \end{eqnarray}
これを使って、こう解きます↓
\begin{eqnarray} \mbox{例3)} & & x^2 +y^2 \\ &=& (x+y)^2 -2xy \\ & & x+y= \sqrt{7} \ , \ xy=3 \ \mbox{を代入して} \\ & & ( \sqrt{7} )^2 -2 \times 3 \\ &=& 7-6 \\ &=& 1 \end{eqnarray}
このように、「\(x+y= \mbox{□}\) , \(xy= \mbox{△}\) のとき、\(x^2 +y^2\) の値を求めよ」なんて問題がでたら、ムリヤリ \( ( \qquad )^2 \) の形に変形すること!
これが、式の値の応用問題の解き方です。
ちなみに、なぜこうした変形ができるかも、中3「多項式」⑥の記事で解説しました。
よーするに、こーゆーことです↓
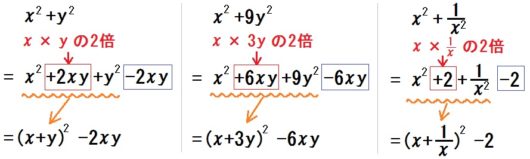
練習問題
以上、平方根における式の値のやり方を解説しました。
- 因数分解や展開をしてから代入する!
- \(x^2 +y^2\) などの値はムリヤリ \( ( \qquad )^2 \) の形に!
こうしたコツを使って問題をたくさん解き、「わかる」を「できる」にしていってください。
ここでも練習問題をちょっとだけ用意したので、どうぞ。
練習2)\(x= \sqrt{5} – \sqrt{3}\) , \(y= \sqrt{5} + \sqrt{3}\) のとき、次の式の値を求めよ。
①\(7x^2 -14xy+7y^2\) ② \( (x-2y)(x-8y) -(x-4y)^2 \)練習3)\(x-y= \sqrt{13}\) , \(xy=5\) のとき、\(x^2 +y^2\) の値を求めよ。
解答:例2)①84 ②-4 例3)23
まとめ
○平方根の近似値の問題は…
≪基本のやり方≫
- ルートの中が自然数→ルートを簡単にする!
- ルートの中が小数→分数になおして有理化!
≪ラクなやり方≫
- 「100」を見つける!
○平方根の式の値の問題は…
- 複雑な式→因数分解や展開をしてから代入する!
- \(x^2 +y^2\) などの式→ムリヤリ \( ( \qquad )^2 \) の形に!
以上、中3「平方根」の応用問題・前半でした。
次回は応用問題・後半として、
・ルートが自然数となるような最小の自然数nを求める
・ルートの整数部分・小数部分をそれぞれ求める
という問題を解説します。
NEXT→中学数学「平方根」のコツ⑥ 最小の自然数n・整数部分と小数部分
[平方根の記事 一覧]
- 中3数学「平方根」のコツ① 平方根とは/平方根の大小
- 中3数学「平方根」のコツ② 有理数と無理数/循環小数と分数
- 中3数学「平方根」のコツ③ 素因数分解/ルートを簡単にする計算
- 中3数学「平方根」のコツ④ 有理化/加減乗除/展開
- 中3数学「平方根」のコツ⑤ 平方根の近似値・式の値
- 中3数学「平方根」のコツ⑥ 最小の自然数n・整数部分と小数部分



コメント