中学数学「平面図形」の作図、3回目です。
前回まで
- 垂直二等分線
- 角の二等分線
- 垂線
- 正三角形
という4つの基本作図が、どんな定義と特徴をもつのか、確認してきました。
そして、これらの応用範囲16コをぜんぶ見てきました。
今回は以上の知識をもとに、高校入試問題12コにチャレンジします。
「高校入試?わたしまだ中1だよ…」
「問題集でも解き方がわからないのに、ムリだ…」
だいじょうぶ。
1回目と2回目の記事をちゃんと読んでいたら、解けます。
信じてついてきてください。
[中学数学「平面図形」の記事一覧]
- 垂直二等分線を使った作図
- 角の二等分線、垂線、正三角形を使った作図
- 作図の高校入試問題を解いてみよう
- 図形の移動
- 円とおうぎ形
復習:作図の解き方

そのまえに、作図問題の解き方のコツをちょっと復習しときましょう。
- 基本作図の特徴もおさえること
- 応用範囲をぜんぶ頭に入れること
- まず完成形をイメージすること
この3つがコツでしたね。
1.基本作図の定義と特徴 一覧
具体的には、
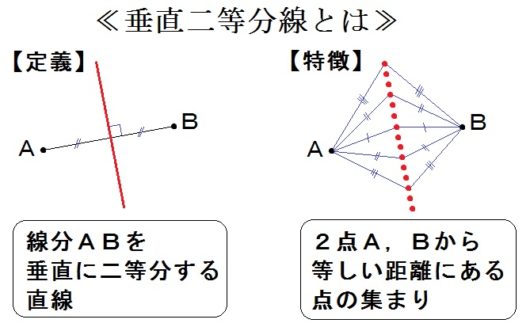
○垂直二等分線
- 【定義】線分を垂直に二等分する直線
- 【特徴】2点から等しい距離にある点の集まり
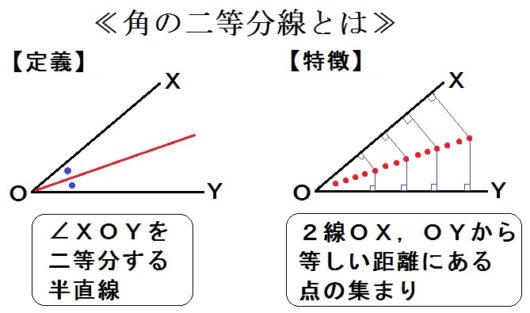
○角の二等分線
- 【定義】角を二等分する半直線
- 【特徴】2直線から等しい距離にある点の集まり
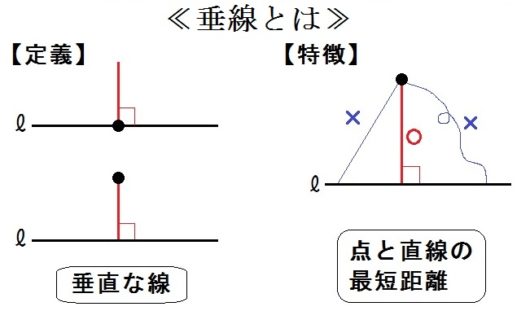
○垂線
- 【定義】垂直な線
- 【特徴】点と直線の最短距離
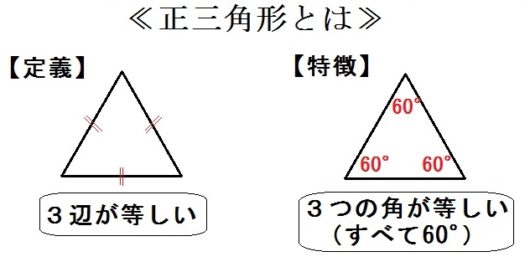
○正三角形
- 【定義】3辺が等しい三角形
- 【特徴】3つの角が等しい(すべて60°)
以上がそれぞれの定義および特徴でした。
いま、ここで、しっかり理解してくださいね。
2.各作図の応用範囲 一覧
また、各作図の応用範囲は以下のとおりでした。
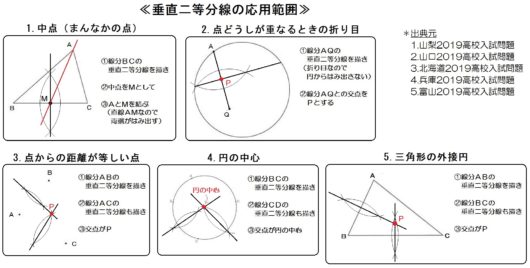
○垂直二等分線の応用範囲
- 中点(まんなかの点)
- 点どうしが重なるときの折り目
- 点からの距離が等しい点
- 円の中心
- 三角形の外接円
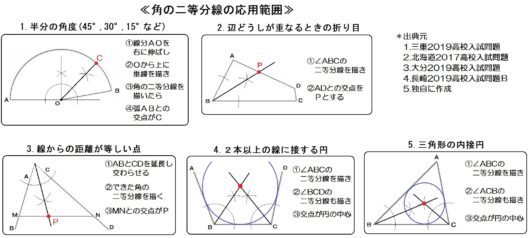
○角の二等分線の応用範囲
- 半分の角度(45°,30°,15°など)
- 辺どうしが重なるときの折り目
- 線からの距離が等しい点
- 2本以上の線に接する円
- 三角形の内接円
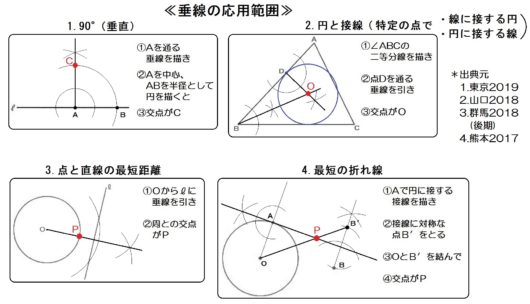
○垂線の応用範囲
- 90°(垂直)
- 特定の点で線に接する円
(または特定の点で円に接する線) - 点と直線の最短距離
- 最短の折れ線
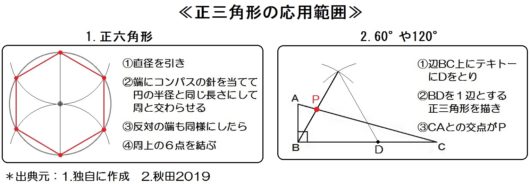
○正三角形の応用範囲
- 正六角形
- 60°や120°
まだ頭に入ってないという中学生は、いま確認して、理解してください。
3.完成形をイメージする
そして、作図問題の解き方のコツ。
3つめは完成形をイメージしてから書き方を考えるというものでした。
どんな難問に出合っても、まず問題文を読んで完成形をおおまかにイメージし、この完成形にたどりつくにはどうしたらいいだろう?どの応用範囲を使えばいいだろう?と考える。
これが最後のコツでした。
復習は終わり。
いよいよ高校入試問題にチャレンジします。
以下、計12題の過去問それぞれ、
問題→ヒント→解答例
という順で示していくので、ぜひ自分で解いてみてください。
ペンとノート、定規とコンパスの準備はいいですか?
Here we go!
Come on bro!
Put some muscle into it!
>Amazonプライム・ビデオ「パシフィック・リム(字幕版)」
こてしらべ問題
まずはこてしらべとして、3問出題します。
難問というほどではないけれど、応用の部類に入る過去問です。
問題をよく読んで、完成形をイメージしてから、どうぞ。
静岡県 入試問題(2018)
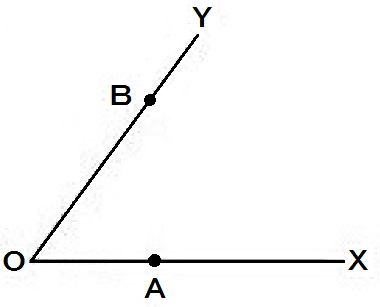
∠AOP=∠BOPであり、2点B,P間の距離が最も短くなる点Pを作図しなさい。
ただし、作図には定規とコンパスを使用し、作図に用いた線は残しておくこと。
2018年度 静岡県 公立高校入試問題 2-3
【ヒント】
- まずは完成形をイメージして書いてみよう
- ∠AOP=∠BOPってことは?
- 直線上のBから最短距離にあるのが点P
…
……
それでは解き方です。
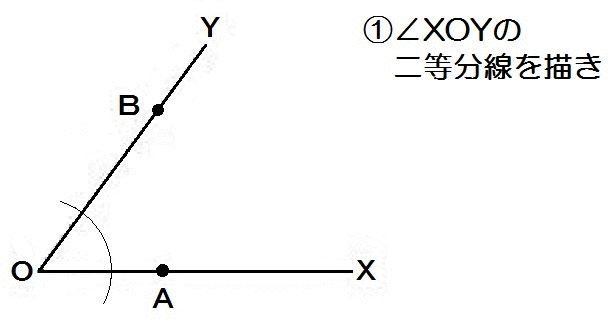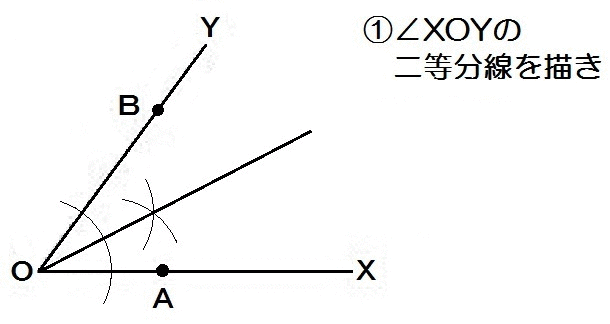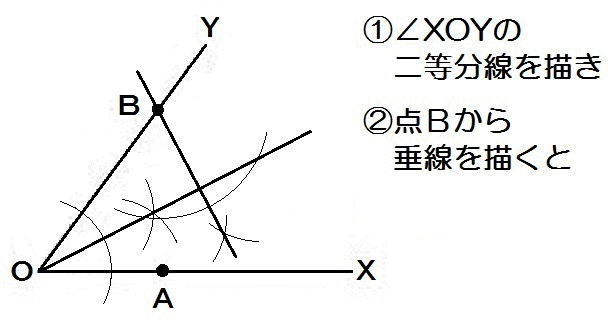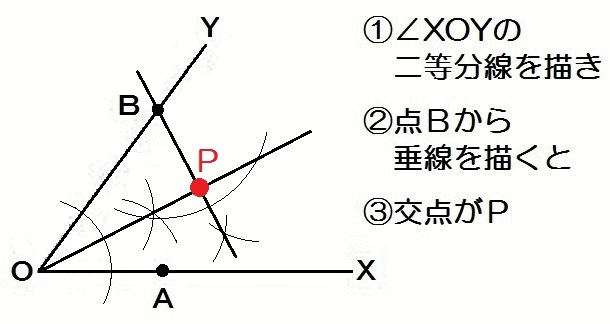
∠AOP=∠BOPなので、まず角の二等分線。
そして直線上のBから最短距離にあるから、垂線を使います。
各作図の定義と特徴、そして応用範囲16コをぜんぶ理解していれば、むずかしくありませんね。
山形県 入試問題(2019)
問2)右図のように、△ABCがあり、点Dは辺AB上の点である。
下の【条件】の①、②をともにみたす点Pを、定規とコンパスを使って作図しなさい。
ただし、作図に使った線は残しておくこと。
【条件】
①線分APの長さは、線分ADの長さと等しい。
②点Pは、直線ABと直線BCから等しい距離にあり、△ABCの外部の点である。
2019年度 山形県 公立高校入試問題 2-4
【ヒント】
- まずは完成形をイメージして書いてみよう
- AP=ADはコンパスで一発
- 2直線から等しい距離にあるってことは?
…
……
それでは解き方です。
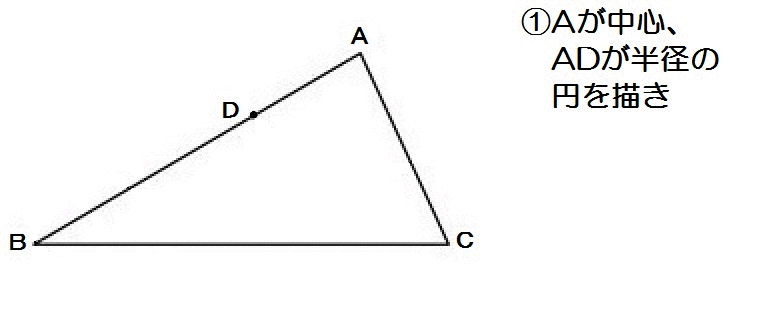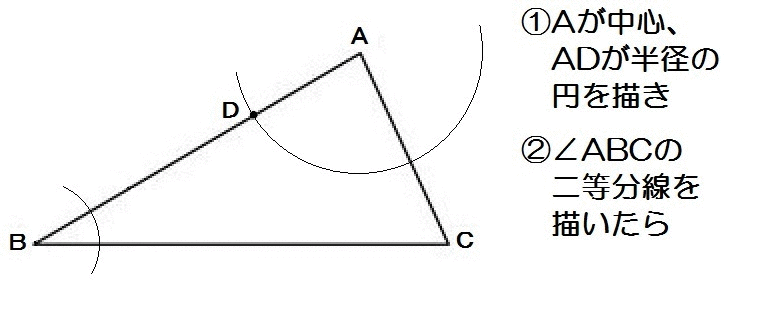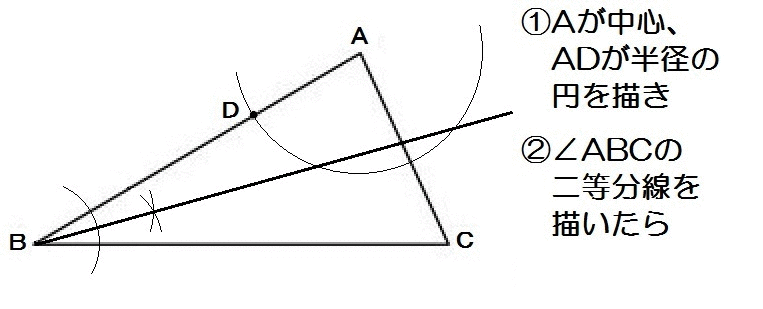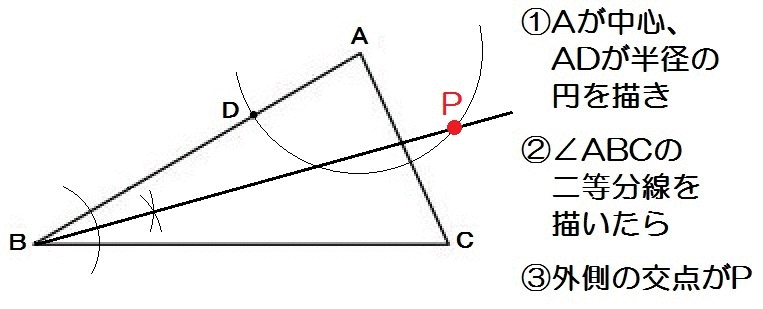
AP=ADだから、Aを中心に円を描く。
んで直線ABとBCからの距離が等しいから、∠ABCの二等分線を描きます。
もちろん順番は逆でもOK。
「2直線から等しい距離にある点の集まり」っていう角の二等分線の特徴が、ここで役立ちましたね。
奈良県 入試問題(2019)
問3)図1の四角形ABCDは平行四辺形である。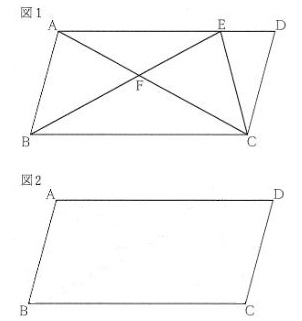
辺AD上に、\(ED= \frac{1}{2}DC\) となる点Eをとり、線分ACと線分BEとの交点をFとする。
点Eを、定規とコンパスを使って図2に作図せよ。
なお、作図に使った線は消さずに残しておくこと。
2019年度 奈良県 公立高校入試問題 4-1改
【ヒント】
- \(\frac{1}{2}DC\) ってDCの半分の長さ
- 線分を半分にするには?
…
……
それでは解き方です。
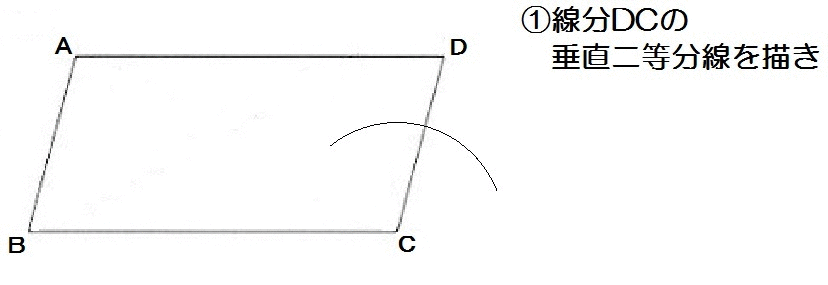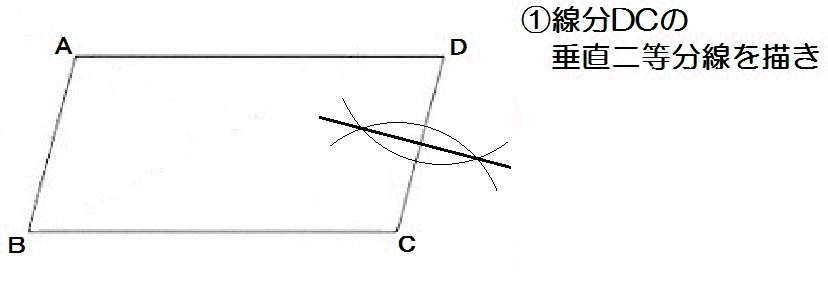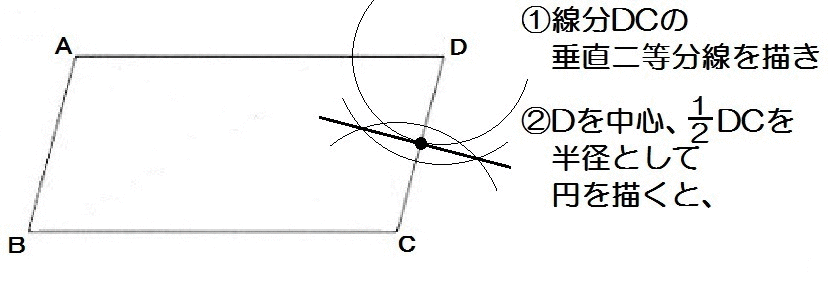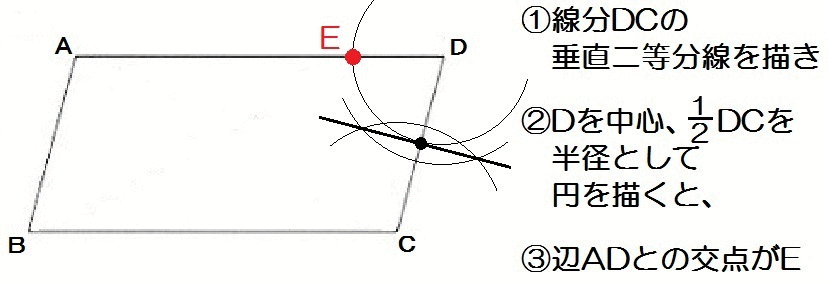
線分DCの垂直二等分線を描いて、\(\frac{1}{2}DC\) をつくる。
んでそれと同じ長さを辺AD上にもってくればいいですね。
ちなみにこの問題、大問4の(1)だけを抜き出したので、点Fとかは作図に関係ありません。あしからず。
以上、こてしらべ問題でした。
不明な点があったらコメント欄からいつでも質問をどうぞ。
つづいて「角度の問題」「円の問題」です。


コメント
2つ目の問題で、なぜ外側の点なのでしょうか?
条件②に「点Pは、直線ABと直線BCから等しい距離にあり、△ABCの外部の点である」とあるためです。
前回同様ですが、
栃木県 入試問題(2018)で、
・Aからもっとも遠い円周上の点は、Aと中心を結んだ先にある
の理由がよくわかりません。
直感的には、それしかないな、とわかるのですが。