連立方程式の文章題、3回目です。
前回につづき、問題パターン別の解き方のコツを解説します。
今回は速さ・時間・道のり問題。
「速さの文章問題が出てくるとお手上げ」
「難しい問題になった途端できなくなる」
こんな中学生の参考にしてください。
つまずく原因と、解き方のコツ

方程式文章題の「速さ・時間・道のり問題」でつまずく原因。
それは2つです。
- 内容の全体像がつかめない
- 速さや単位変換への苦手意識
よって、「速さ・時間・道のり問題」が苦手な中学生は、以下2つのコツをマスターするだけで、できるようになります。
1.表のような線分図を描くこと
2.単位は速さに合わせること
このコツはすべての速さ問題に使えます。例外はありません。
また連立方程式だけでなく、1次方程式の速さ問題でも同様です。
(詳しくは以下の記事を参照)
以下では、このコツを具体的にどのように使うのか、
- 途中で速さが変わる問題
- 池の周囲をまわる問題
- 列車の問題
という3パターン別にそれぞれ解説していきます。
なお、そもそも単位変換が苦手という中学生は小学校内容の復習が必要です。
上に挙げた1次方程式文章題⑥の記事中に、その復習問題も入っていますので、「15分が何時間かわからない」という生徒はそちらをまず解いてからこの記事に戻ってきてください。
途中で速さが変わる問題

- 表のような線分図を描く
- 単位は速さに合わせる
このコツをどのように使うのか、まずは「途中で速さが変わる問題」で見ていきましょう。
解き方
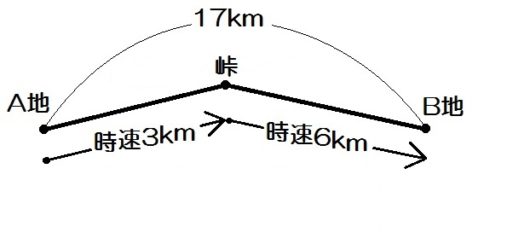
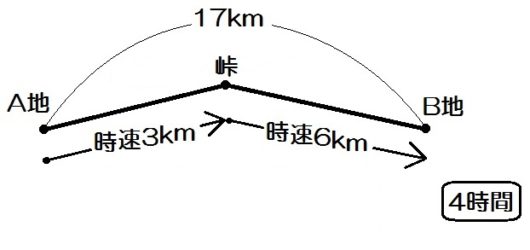
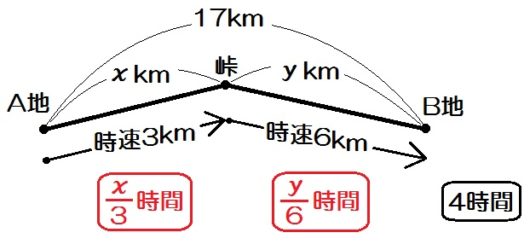
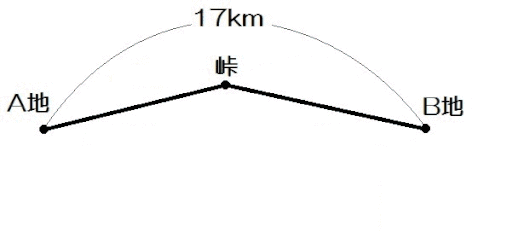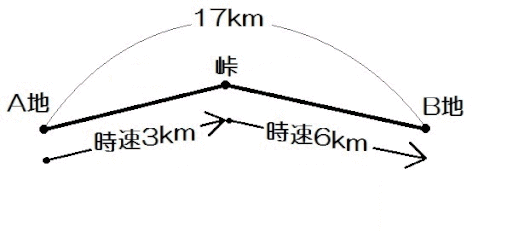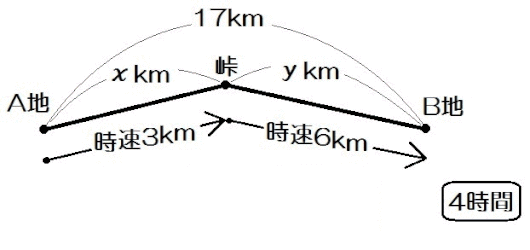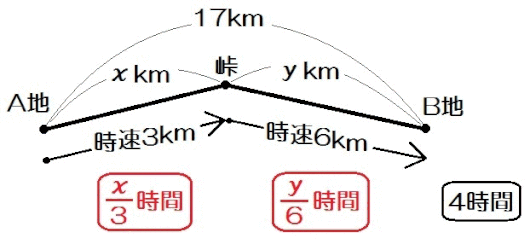
例題1)藤村くんがA地から峠をこえて17km離れたB地に行った。A地から峠までは時速3km、峠からB地までは時速6kmで歩いたら、全体でちょうど4時間かかった。A地から峠までと、峠からB地までの道のりはそれぞれ何kmか。
最初に、求めるものを \(x , y\) で置きましょう。
例題1では「A地から峠までを \(x\) km、峠からB地までを \(y\) kmとする。」等ですね。
次に、文章に沿って表のような線分図を描いていきます。
こんな感じ↓
「藤村くんがA地から峠をこえて17km離れたB地に行った。」
「A地から峠までは時速3km、峠からB地までは時速6kmで歩いたら」
「全体でちょうど4時間かかった。」
「A地から峠までを \(x\) km、峠からB地までを \(y\) kmとする。」
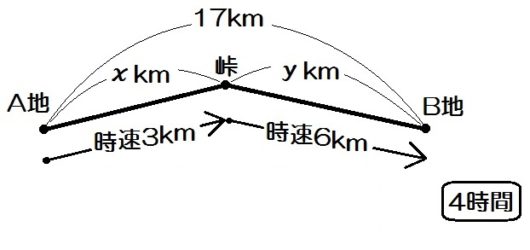
このように、「線の上」「線のすぐ下」「さらに下」と3段にわけて、それぞれ「道のり」「速さ」「時間」を書きこんでいく。
ジュウゴの場合は上から順に道のり・速さ・時間と決めていますが、どこに何を書くかは自分で決めてかまいません。
とにかく、「いちばん上は道のりの段」等と決めたら、それをやぶらない。
これがわかりやすい線分図を描く秘訣です。
ここまで描けたら、次に、まだ埋まっていない箇所を書きこみます。
A地~峠の「時間」と、峠~B地の「時間」がまだですね。
よって、こう↓
これで、表のようにわかりやすい線分図が完成しました。
あとは、自分で描いたこの線分図を見て、方程式を2つ作るだけ。
つまり等しい関係を2通り見つけるだけです。
等しい関係のパターンは、連立方程式 文章題①でもお話したように、
- 「○と△を合わせると□」
- 「○は△より□小さい(大きい)」
- 「○は△と等しい」
のどれかですね。
……見つかりましたか?
\begin{eqnarray} \left\{ \begin{array}{l} x+y=17 \\ \frac{x}{3} + \frac{y}{6} =4 \end{array} \right.\end{eqnarray}
以上のように、連立方程式の道のり文章題では、
- 文章に沿って「道のり」「速さ」「時間」を3段にわけた、表のような線分図を描く
- まだ埋まっていない個所を \(x ,y\) も使って埋める
- 等しい関係を2つみつける
この手順で、必ず連立方程式が作れます。
もういちど、線分図の描き方をアニメーションにしました。例題の文章と照らし合わせながら、自分が描くつもりでイメージしてみてください。
(ちなみに例題1の答えはA~峠…7km、峠~B…10km)
単位変換のある類題
例題2)嬉野くんは家から36km離れたカフェまでを往復する。行きは家から2時間歩き、42分間自転車に乗ってカフェに着いた。帰りは行きと同じ速さでカフェから1時間歩き、48分間自転車に乗って家に着いた。歩く速さ、自転車の速さはそれぞれ時速何kmか。
では、単位変換の必要な問題もやってみましょう。
この例題2などがそれです。
とりあえずは求めるものを \(x , y\) で置くので、「歩く速さを時速 \(x\) km、自転車の速さを時速 \(y\) kmとする。」等とします。
さて、例題1と同様に、文章に沿って線分図を描いてみましょう。
ジュウゴなら、こう描きます↓
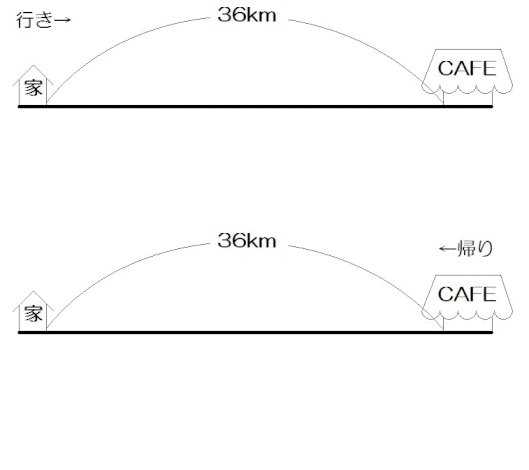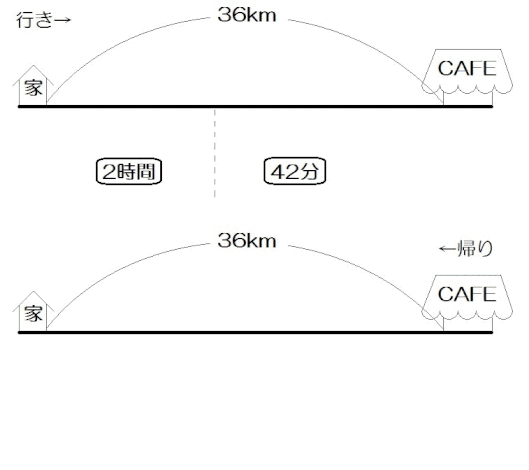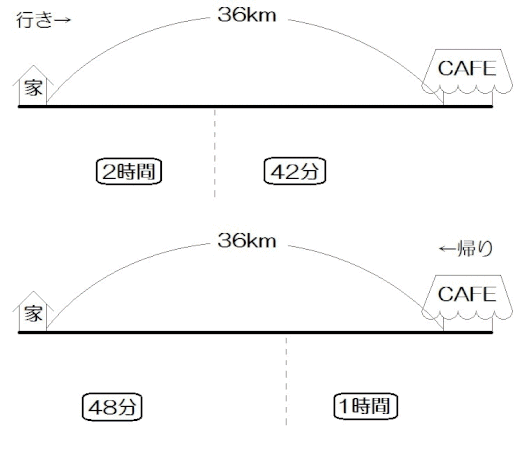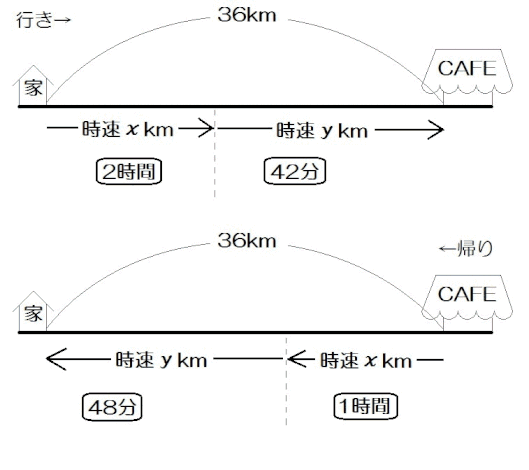
往復の問題なので、行きと帰り、線を2本描きました。
ここまで描けたら、次に埋まっていない個所を埋めていきますが、その前に「単位がそろってない!」と気づきますね。
ここでもうひとつのコツです。
単位は速さに合わせる。
つまり例題2なら、「時速○km」なので、時間は「何時間」に、道のりは「何km」に合わせるんです。
いま、道のりは36kmと合ってるので、42分と48分をそれぞれ時間に直します。
$$ 42 \mbox{(分)} = \frac{42}{60} \mbox{(時間)} = \frac{7}{10} \mbox{(時間)} $$
$$ 48 \mbox{(分)} = \frac{48}{60} \mbox{(時間)} = \frac{4}{5} \mbox{(時間)} $$
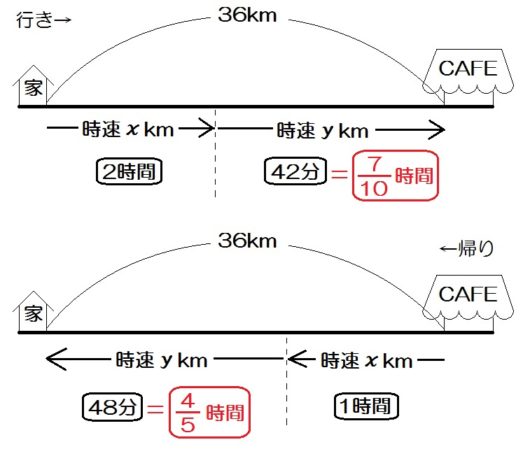
あとは埋まっていない個所を \(x , y\) も使って埋めましょう。
速さ・時間はもう埋まっているので、残りは道のりですね。
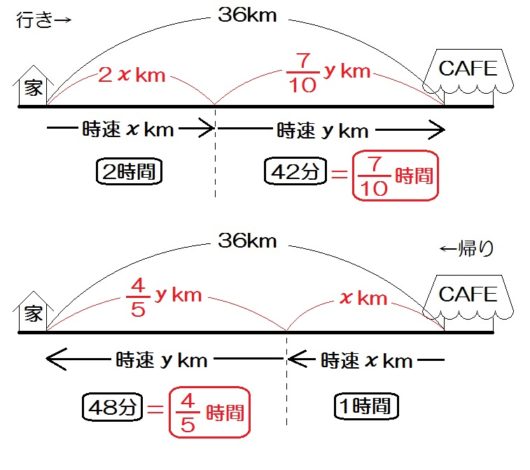
こうして線分図が完成します。
もう、等しい関係はすぐわかるでしょう。
\begin{eqnarray} \left\{ \begin{array}{l} 2x+ \frac{7}{10}y = 36 \\ \frac{4}{5}y + x = 36 \end{array} \right.\end{eqnarray}
以上のように、単位変換が必要な問題では、速さに単位を合わせる。
これが連立方程式の道のり問題におけるもうひとつのコツになります。
(例題2の答えは、歩く速さ…時速4km、自転車の速さ…時速40km)
練習問題
それでは、途中で速さが変わる問題を2問用意しました。
ぜひチャレンジしてみてください。
解答は末尾に記載。
また質問はコメント欄からどうぞ。
問1)ヨシさんはA地から140km離れたC地まで自動車で行った。A地から途中のB地までは時速40km、B地からC地までは時速80kmで走って、全体で2時間かかった。A地からB地までと、B地からC地までの道のりはそれぞれ何kmか。
問2)ロビンソンはA地から84km離れたB地にバスと列車を使って行った。A地から15分間バスに乗り、そのあと列車に42分乗ってB地に着いた。このとき列車の速さはバスの速さのちょうど \(\frac{5}{2}\) 倍だった。バスと列車の速さはそれぞれ分速何mか。なお、乗り換えの時間は考えないものとする。
問1)A~B…20km、B~C…120km
問2)バス…分速700m、列車…分速1750m
なお、連立方程式の計算がよくわからないという場合は以下の記事から復習してください。
池の周囲をまわる問題

「途中で速さが変わる問題」の次は、「池の周囲をまわる問題」です。
例題3のような問題も連立方程式文章題では頻出しますが、やはり表のような線分図を描く、単位は速さに合わせるのがコツになります。
そしてまわる問題における等しい関係は
- AとBが逆方向に進んで出会う
→(Aの道のり)+(Bの道のり)=1周分 - 同じ方向に進んでAがBに追いつく
→(Aの道のり)-(Bの道のり)=1周分
の2パターンと決まっています。
解き方
例題3)池のまわりに1周4000mの道路がある。兄は走って、弟は自転車でまわる。兄と弟が逆方向に同時に出発すると10分後に出会い、同じ方向に出発すると50分後に弟は兄を1周遅れにする。兄と弟の速さをそれぞれ求めよ。
「兄の速さを分速 \(x\) m、弟の速さを分速 \(y\) mとする。」
これはいいですね。
次に線分図を描きますが、学校でも塾でも、下のような図を習ったんじゃないでしょうか。
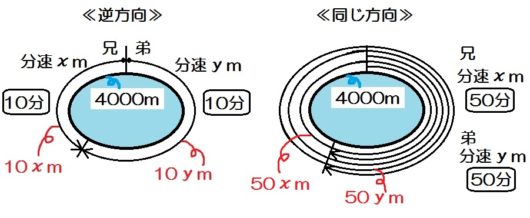
この図でもいいんですが、ごちゃごちゃしてわかりにくくないですか?
それでジュウゴは近年、(1次方程式文章題のときでも話しましたが)まっすぐな線分図をおススメしています。
逆方向に進んで出会う場合は、出発点を両端に分けて。
同じ方向に進んで出会う場合は、出発点を同じにして。
こういう図です↓
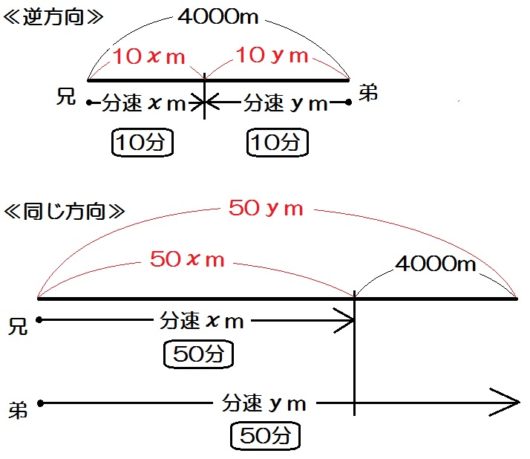
逆方向に進んで出会うということは、2人の道のりを合わせたらちょうど池1周分。
同じ方向に進んで追いつくということは、弟が兄よりちょうど池1周分多く進む。
だからこのような線分図になります。
そしてこの図のほうが、「道のり」「速さ」「時間」の3段すべてがわかりやすく、また埋まっていない個所も一目瞭然です。
連立方程式、できますね。
\begin{eqnarray} \left\{ \begin{array}{l} 10x+10y=4000 \\ 50y-50x=4000 \end{array} \right.\end{eqnarray}
以上のように、池の周囲をまわる問題であっても、表のような線分図を描く。
そして
- 逆方向:2人の道のりの和
- 同じ方向:2人の道のりの差
で等式をつくる。
これが解き方です。
(例題3の答えは兄…分速160m、弟…分速240m)
単位変換のある類題
例題4)周囲が3kmの池のまわりを、Aは自転車で、Bは徒歩で、同じ地点から逆方向にまわる。二人が同時に出発すると15分後に出会い、AがBよりも20分遅れて出発すると、Aが出発してから10分後に二人は出会う。A,Bの速さはそれぞれ分速何mか。
ここまでくればもう、新しく言うことはありません。
例題4を自力で解いてみてください。
…。
……。
では、最初から最後までの解答例です。
Aの速さを分速 \(x\) m、Bの速さを分速 \(y\) mとする。
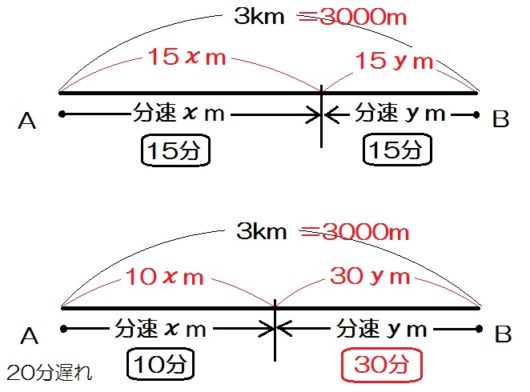
\begin{eqnarray} \left\{ \begin{array}{l} 15x+15y=3000 \ \large{\mbox{…①}} \\ 10x+30y=3000 \ \large{\mbox{…②}} \end{array} \right.\end{eqnarray}
①÷15で \(x+y=200 \ \large{\mbox{…①’}} \)
②÷10で \(x+3y=300 \ \large{\mbox{…②’}} \)
①’-②’で
\begin{eqnarray} -2y &=& -100 \\ y &=& 50 \ \large{\mbox{…③}}\end{eqnarray}
③を①’に代入して
\begin{eqnarray} x+50 &=& 200 \\ x &=& 150\end{eqnarray}
答.A…分速150m、B…分速50m
練習問題
それでは、池の周囲をまわる練習問題も2つ用意しました。
- 表のような線分図を描く
- 単位は速さに合わせる
- 「逆方向:道のりの和」/「同じ方向:道のりの差」で立式
という3つのコツを使って、やっつけてください。
解答は末尾に記載、質問はコメント欄からどうぞ。
問3)周囲が3600mの池のまわりを、春日くんと若林くんが同じ地点から一定の速さでまわる。反対方向にまわると15分後に出会い、同じ方向にまわると30分後に春日くんが若林くんに追いつく。二人の速さはそれぞれ分速何mか。
問4)周囲が4kmの湖のまわりを、伊達くんと冨澤くんが同じ地点から一定の速さでまわる。反対方向にまわると25分で出会い、同じ方向にまわると1時間40分後に伊達くんが冨澤くんに追いつく。二人の速さはそれぞれ毎分何mか。
問3)春日…分速180m、若林…分速60m
問4)伊達…毎分100m、冨澤…毎分60m
≪関連記事一覧≫
- 連立方程式 文章題①【立式のコツ】
- 連立方程式 文章題②【整数、平均、過不足問題】
- 連立方程式 文章題④【割合の問題】
- (数学指導法の記事一覧はまとめページへ)
列車の問題

最後に「列車の問題」の解き方を解説します。
例題5のような列車の問題においても、やはり
- 表のような線分図を描く
- 単位は速さに合わせる
というコツは変わりません。
そのうえで、列車の進んだ道のりに注意して線分図を描くというのがポイントになります。
解き方
例題5)ある列車が、570mの鉄橋を渡りはじめてから渡り終わるまでに30秒かかった。また、この列車が、1820mのトンネルに入りはじめてから出終わるまでに80秒かかった。この列車の長さと秒速をそれぞれ求めよ。
「列車の長さを \(x\) m、秒速 \(y\) mとする。」
この一文を書いてから、線分図を描きます。
ここで注意すべきは列車の進んだ道のり。
鉄橋も、トンネルも、列車の先頭が入りはじめてから出終わるまで進んでいますね。よって下のような線分図になります。
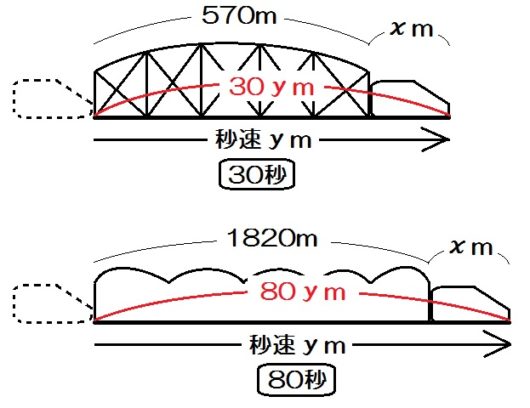
つまりどちらも、列車の長さ分だけ多く進んでいるということ。
よって、連立方程式は
\begin{eqnarray} \left\{ \begin{array}{l} 30y=570+x \\ 80y=1820+x \end{array} \right.\end{eqnarray}
となります(もちろん左辺と右辺が逆でもOK)。
以上のように、列車の問題では、問題文をよく読んで列車の進んだ道のりに注意すること。
これがポイントです。
(例題5の答えは、列車の長さ…180m、速さ…秒速25m)
単位変換のある類題
例題6)長さ150mの列車Aと、長さ90mの列車Bが、出会ってからすれちがうまでに6秒かかる。また列車Aが列車Bに追いついてから完全に追いぬくまでにちょうど1分かかる。列車A,Bそれぞれの秒速を求めよ。
では、単位変換のある類題として、列車がすれちがったり追い越したりする場合もやっつけましょう。
例題6などがそれです。
とりあえずは「列車Aを秒速 \(x\) m、列車Bを秒速 \(y\) mとする。」
ここで、乗り物がすれちがったり追い越したりする場合のコツもお伝えします。
それは片方の乗り物を停まったものとして考えること。
たとえばあなたが高速道路を時速80kmで走っているとします。そして時速100kmの対向車とすれちがうとします。このとき、仮にあなたの車を停まったものとして考えると、対向車の速さは \(80+100=180\) kmに感じられます。
また、あなたが高速道路を時速80kmで走っていて、時速100kmの車に追い越されました。このとき、仮にあなたの車を停まったものとして考えると、追い越した車の速さは \(100-80=20\) kmに感じられます。
つまり逆方向ですれちがうときには速さの足し算。
同じ方向で追い越すときには速さの引き算。
これが、片方の乗り物を停まったものとして考えたときの、速さなんです。
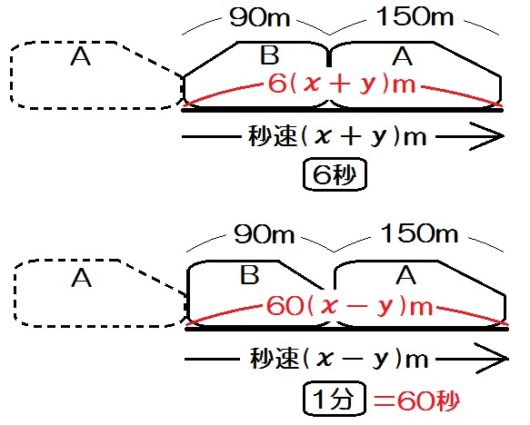
例題6、こんな線分図を描けるというのが、わかるでしょう。
上の図は列車Bを停まったものと考えて、すれちがう場合。
下の図はやはり列車Bを停まったものと考えて、AがBを追い越す場合です。
そしてどちらも、列車Aの進んだ道のりは \(90+150\) 、つまり2台の列車の長さ分というのがわかります。
よって、連立方程式は
\begin{eqnarray} \left\{ \begin{array}{l} 6(x+y)=90+150 \\ 60(x-y)=90+150 \end{array} \right.\end{eqnarray}
以上のように、列車がすれちがう/追いつき追い越す問題では、片方を停まったものとして考える、そのうえで
- すれちがうときは速さの足し算
- 追い越すときは速さの引き算
これがポイントになります。
(例題6の答えは A…秒速22m、B…秒速18m)
練習問題
ちなみに、なぜ片方を停まったものとして考えるのか?
人間の思考というのは2つ以上の運動をそのまま捉えるようにはできていないからです。
だから数学にかぎらず、たとえば物理の問題でも、困ったらこの「片方を停まったものと考えてみる」というコツを使ってみてください。
それでは、最後の練習問題です。
解答は末尾に記載、質問はコメント欄からどうぞ。
問5)長さ146mの列車Aが、あるトンネルに入りはじめてから出終わるまでに92秒かかった。このトンネルを、長さ151mの列車Bが、秒速を1mだけ早くして通過すると、入りはじめてから出終わるまでに89秒かかった。トンネルの長さと列車Aの秒速をそれぞれ求めよ。
問6)長さの同じ列車A,Bがある。BはAの1.5倍の速さで走り、AとBがすれちがうのに10秒かかる。また、列車Aは長さ950mの鉄橋を渡りはじめてから渡り終わるまでにちょうど1分かかる。列車Aの長さと秒速をそれぞれ求めよ。
問5)トンネル…2430m、速さ…秒速28m
問6)長さ…250m、速さ…秒速20m
>Amazonプライム・ビデオで「僕達急行 A列車で行こう」を観る
≪関連記事一覧≫
- 連立方程式 文章題①【立式のコツ】
- 連立方程式 文章題②【整数、平均、過不足問題】
- 連立方程式 文章題④【割合の問題】
- (数学指導法の記事一覧はまとめページへ)
まとめ

中学数学 連立方程式 文章題の「速さ・時間・道のり問題」。
解き方のコツは
- 表のような線分図を描く
- 単位は速さに合わせる
そのうえで、
途中で速さが変わる問題では、往復する場合は線を2本描くといい。
池の周囲をまわる問題では、「逆方向:道のりの和」/「同じ方向:道のりの差」で立式する。
列車の問題では、列車が進んだ道のりに注意する。またすれちがう/追い越す場合は片方を停まったものと考えて、速さの足し算/引き算をする。
次回は「割合の問題」の解き方を解説します。
食塩水の問題がわからない…。
生徒数の増減問題がチンプンカンプン…。
定価や利益って言葉が出ただけでイヤ…。
こんな中学生の参考にしてください。






コメント
全ての練習問題に解き方をつけてほしいです。
問3問4についてなのですが、
答えが逆になってしまいます。
数字は合っているけど、春日くんと若林くんの答えが逆。
伊達くんと冨澤くんの答えが逆という状況です。
どうしてでしょうか。
いつも参考にしております。
また以前は返信ありがとうございました。
今回も質問なのですが
問2 問6 の立式から答えまでの解法を
教えて頂きたいです。
よろしくお願いいたします。
>す様
遅くなりました。
問2)バスの速さを分速xm、列車の速さを分速ymとする。
y=2分の5 x ・・・①
15x+42y=84000・・・②
②を整理して
5x+14y=28000・・・②’
②’に①を代入して
5x+35x=28000、解いてx=700・・・③
③を①に代入してy=1750
問6)
列車Aの長さをxm、速さを秒速ymとすると、
列車Bの長さはxm、速さは秒速1.5ym。
10(y+1.5y)=2x・・・①
60y=950+x・・・②
両方を整理して
2x-25y=0・・・①’
x-60y=950・・・②’
①’-②’×2で
95y=1900、y=20・・・③
③を①’に代入して
2x-500=0、x=250
ほかにもいろいろ解法はありますがとりあえず一例のみ。
いつも参考にさせていただいています。
書き間違いかな?と思うところを見つけました。
例題6の連立方程式ですが、
6(x+y)=90+150
60(x+y)=90+150
このように書かれていますが、
60(x-y)=90+150 ではないかと思います。
お時間のあるときにご確認いただければ幸いです。
>みずがめさま
そのとおりです、ミスってました…。
ご指摘ありがとうございます、修正します。
また別記事でコメントいただいた1次関数も、なかなか書けずすみません。
近いうちにいつか、とは思っていますm(_ _)m
練習問題全てに解き方を書いてください。答えがあっていたとしても。解き方が違ったりするかもしれませんし、解き方を見て、活かしたい方です