中学数学のつまずき解消をめざすこの連載。
中3「平方根」の3回目は素因数分解とルートを簡単にする計算を扱います。
つまり
$$ 20= 2^2 \times 5 $$
$$ \sqrt{20} = 2 \sqrt{5} $$
という2つ。
そして記事の後半では、この先の平方根の計算でつまずかないための大事なコツを紹介します。
中学生のみならず講師や保護者の方もご参考ください。
素因数分解
まず、素数とは・素因数分解とは何か?
また素因数分解のやり方を解説します。
2021年度からの新学習指導要領ではこの素因数分解、中1に移行しますが、素因数分解をじっさいに使うのは平方根単元です。
なので、この記事ではこのタイミングでやります。
なぜ「素因数分解」単元が中1に移行されたのかよくわかりません。おそらく「誤差・近似値・有効数字」単元が中3に移行するので、その代わりでしょうね。
素数とは・素因数分解とは
素数とは「1および自分自身でしか割れない自然数」のこと。
つまり約数がふたつだけの数のことで、ようするに以下の数たち。
\begin{eqnarray} & &2 \quad 3 \quad 5 \quad 7 \\ & &11 \quad 13 \quad 17 \quad 19 \\ & &23 \quad 29 \quad 31 \quad 37 \cdots \end{eqnarray}
「4」は1と4以外にも2で割れるから素数じゃない。
「6」は1と6以外にも2や3を約数にもつから、素数じゃない。
「9」は1と9以外にも3を約数にもつから、やはり素数じゃない。
こんなふうに、1および自分自身以外でも割れる数を消去していって、素数が出てきます。
ちなみに「1」は素数じゃありません。約数が1のひとつだけだから。
そして素因数分解とは、自然数を素数の積の形にすること。
つまり素数のかけ算に分解することで、ようするに以下のような変形。
\begin{eqnarray} 6 &=& 2 \times 3 \\ 9 &=& 3^2 \\ 12 &=& 2^2 \times 3 \\ 1300 &=& 2^2 \times 5^2 \times 13 \end{eqnarray}
これが素因数分解。
ちなみに1以外の自然数はすべて、素数の積の形(または素数そのもの)で表すことができます。
なので、素数って自然数の世界における原子みたいなもの。
だからわざわざ「素数」と名付けられてるわけです。
[関連記事]
科学の歴史の流れを超簡単にまとめてみた① 18~20世紀
素因数分解のやり方
では、素因数分解はどうやればいいか?
百聞は一見に如かず。
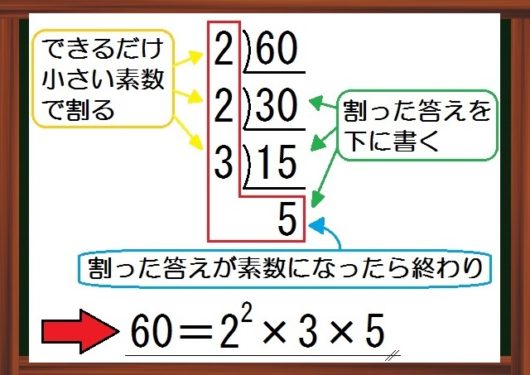
例として「60」を素因数分解してみましょう↓

素因数分解のやり方
さいごは、L字型のところに出ている素数たちをかけ算でつなげばいいんです。
ちなみに素数 \(2\) はふたつあるので、
\( 60= 2 \times 2 \times 3 \times 5\)
じゃなくて
\( 60= 2^2 \times 3 \times 5\)
と、指数をつかって書くようにしましょう。
では練習問題として、以下みっつの数を素因数分解してみてください。
- \(96\)
- \(273\)
- \(275\)
…。
解答は以下のとおり。
- \(96= 2^5 \times 3\)
- \(273= 3 \times 7 \times 13\)
- \(275= 5^2 \times 11\)
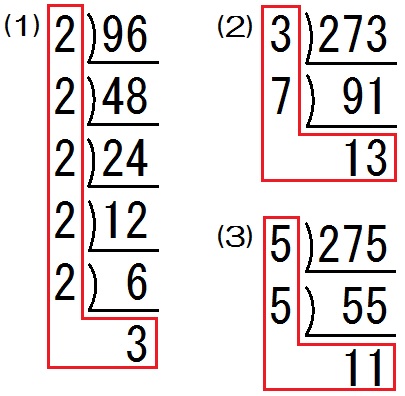
素因数分解の練習問題 解答
やってみてわかったでしょう。
素数は覚えてしまったほうがいいと。
とくに40以下の素数はよく出てきます。
\begin{eqnarray} & &2 \quad 3 \quad 5 \quad 7 \\ & &11 \quad 13 \quad 17 \quad 19 \\ & &23 \quad 29 \quad 31 \quad 37 \cdots \end{eqnarray}
素因数分解ができるためにも、37までの素数はこの機会に覚えてしまいましょう。
[平方根の記事 一覧]
- 中学数学「平方根」のコツ① 平方根とは/平方根の大小
- 中学数学「平方根」のコツ② 有理数と無理数/循環小数と分数
- 中学数学「平方根」のコツ③ 素因数分解/ルートを簡単にする計算
- 中3数学「平方根」のコツ④ 有理化/加減乗除/展開
- 中3数学「平方根」のコツ⑤ 平方根の利用・応用問題
平方根のかけ算・わり算
次に、ルートの中身を簡単にする計算です。
ただルートを簡単にする方法を理解するには、まず平方根のかけ算・わり算を知らなければいけません。
ってことで、ルートのかけ算・わり算から見ていきましょう。
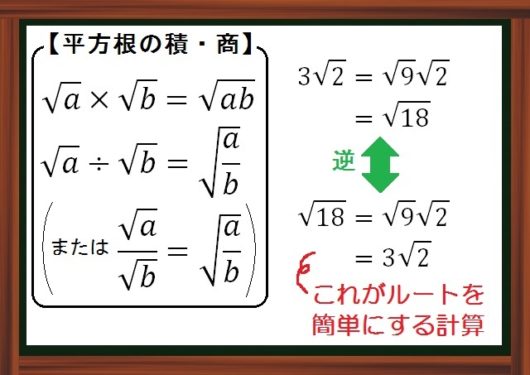
平方根のかけ算・わり算のルール
これが平方根のかけ算・わり算のルールです。
つまりルートの中身をかけ算・わり算できるってこと。
文字を使って一般的に表せば↓
となります。
なお、わり算のほうは÷記号の代わりに分数で
とも表せる。
だから例えば、こんな割り切れない計算でも↓
$$ \frac{\sqrt{20}}{\sqrt{14}} = \sqrt{\frac{20}{14}} = \sqrt{\frac{10}{7}} $$
となります。
また、かけ算のほうは×記号を省略して
$$ \sqrt{6} \sqrt{7} = \sqrt{42} $$
と書くこともあります。
\(3 \sqrt{2}\) を \(\sqrt{a}\) の形で表す
さてここで、\(3 \sqrt{2}\) を \(\sqrt{a}\) の形で表してみましょう。
\(3 = \sqrt{9}\) だから、
$$ 3 \sqrt{2} = \sqrt{9} \sqrt{2} = \sqrt{18} $$
とできます。
じゃあ逆に、
$$ \sqrt{18} = \sqrt{9} \sqrt{2} = 3 \sqrt{2} $$
ともできる。つまり
$$ \sqrt{18} = \sqrt{3^2} \sqrt{2} = 3 \sqrt{2} $$
同様にして
\begin{eqnarray} \sqrt{20} &=& \sqrt{2^2} \sqrt{5} = 2 \sqrt{5} \\ \sqrt{48} &=& \sqrt{4^2} \sqrt{3} = 4 \sqrt{3} \end{eqnarray}
こういうのがルートを簡単にする計算なんです。
>Amazonプライム・ビデオ「簡単なお仕事です。に応募してみた」
ルートの中を簡単にする計算
以上からわかるように、ルートを簡単にするには2乗を見つければいい。
では、どうやって見つけるか?
ここで素因数分解を使うんです。
ルートの中身を素因数分解
論より証拠。
たとえば \(\sqrt{18}\) や \(\sqrt{20}\) を簡単にするには、こうやります↓
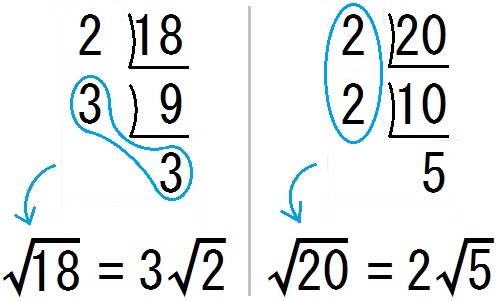
また \(\sqrt{48}\) を簡単にするには、こうやります↓
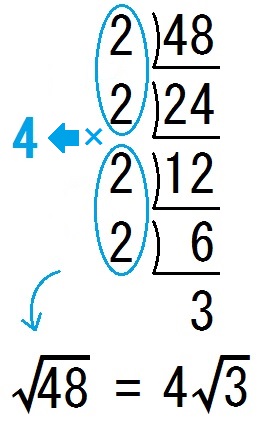
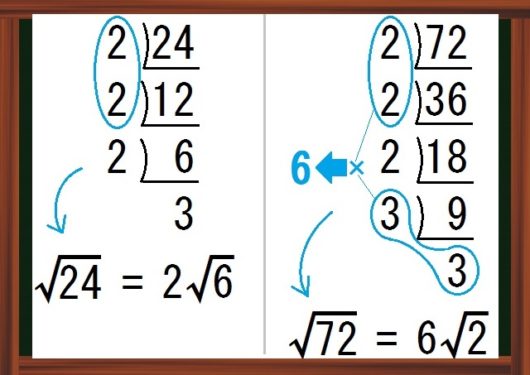
そして \(\sqrt{24}\) や \(\sqrt{72}\) を簡単にするには、こうやります↓
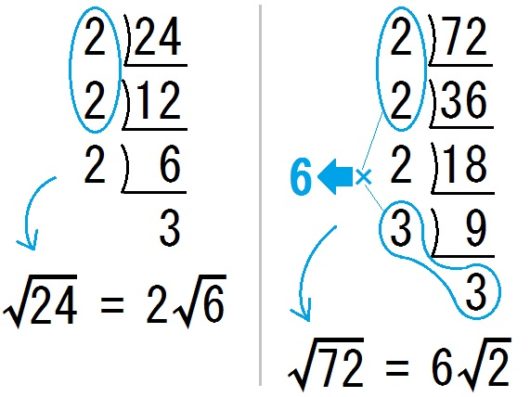
つまり、1ペアをできるだけたくさん作って、ルートの外に出してやればいい。
正確に書けば、\(\sqrt{24}\) や \(\sqrt{72}\) の計算はこうなっています↓
\begin{eqnarray} \sqrt{24} &=& \sqrt{2^2 \times 2 \times 3} \\ &=& \sqrt{2^2} \sqrt{2 \times 3} \\ &=& 2 \sqrt{6} \end{eqnarray}
\begin{eqnarray} \sqrt{72} &=& \sqrt{2^2 \times 3^2 \times 2} \\ &=& \sqrt{2^2} \sqrt{3^2} \sqrt{2} \\ &=& 2 \times 3 \times \sqrt{2} \\ &=& 6 \sqrt{2} \end{eqnarray}
しかし、こんな複雑な式をダラダラと書くよりも、素因数分解の筆算のところにマークしてしまったほうがよっぽど速い。
だから中学生のみなさんは、素因数分解の筆算を横に書いて、
- \( \sqrt{18} = 3 \sqrt{2}\)
- \( \sqrt{20} = 2 \sqrt{5}\)
- \( \sqrt{48} = 4 \sqrt{3}\)
- \( \sqrt{24} = 2 \sqrt{6}\)
- \( \sqrt{72} = 6 \sqrt{2}\)
とイッパツで出すようにしましょう。
練習してみよう
では、ルートを簡単にする計算を練習してみましょう。
素因数分解を使って、イッパツで出してみてください。
練習問題)次の数を、√の中をできるだけ簡単な整数で表せ。
(1) \(\sqrt{12}\) (2) \(\sqrt{27}\)
(3) \(\sqrt{28}\) (4) \(\sqrt{32}\)
(5) \(\sqrt{44}\) (6) \(\sqrt{45}\)
(7) \(\sqrt{50}\) (8) \(\sqrt{60}\)
(9) \(\sqrt{68}\) (10) \(\sqrt{98}\)
…。
それでは解答です。
(1) \(\sqrt{12} = 2 \sqrt{3}\) (2) \(\sqrt{27} = 3 \sqrt{3}\)
(3) \(\sqrt{28} = 2 \sqrt{7}\) (4) \(\sqrt{32} = 4 \sqrt{2}\)
(5) \(\sqrt{44} = 2 \sqrt{11}\) (6) \(\sqrt{45} = 3 \sqrt{5}\)
(7) \(\sqrt{50} = 5 \sqrt{2}\) (8) \(\sqrt{60} = 2 \sqrt{15}\)
(9) \(\sqrt{68} = 2 \sqrt{17}\) (10) \(\sqrt{98} = 7 \sqrt{2}\)
ここで大事なコト。
それは、このさきの平方根の計算(有理化・加減乗除・展開)でつまずかないためには、こうしたルートを簡単にする計算が10秒以内にできなければいけないというコトです。
そうでないと、テスト時間内に解き終わりません。
そして、そのためのコツは2つあります。
ひとつは先述したとおり、37までの主な素数は覚えてしまうこと。
もうひとつは、\(\sqrt{50}\) までの簡単にできる平方根も覚えてしまうことです。
\(\sqrt{50}\) までは覚えてしまおう!
\(\sqrt{50}\) までの、ルートが簡単になる平方根は以下のとおりです。
- \(\sqrt{8} = 2 \sqrt{2}\)
- \(\sqrt{12} = 2 \sqrt{3}\)
- \(\sqrt{18} = 3 \sqrt{2}\)
- \(\sqrt{20} = 2 \sqrt{5}\)
- \(\sqrt{24} = 2 \sqrt{6}\)
- \(\sqrt{27} = 3 \sqrt{3}\)
- \(\sqrt{28} = 2 \sqrt{7}\)
- \(\sqrt{32} = 4 \sqrt{2}\)
- \(\sqrt{40} = 2 \sqrt{10}\)
- \(\sqrt{44} = 2 \sqrt{11}\)
- \(\sqrt{45} = 3 \sqrt{5}\)
- \(\sqrt{48} = 4 \sqrt{3}\)
- \(\sqrt{50} = 5 \sqrt{2}\)
この13個はよく問題に出るので、もう覚えてしまいましょう。
そうすれば、たとえば以下の計算が一瞬でできるようになります。
\begin{eqnarray} & & \sqrt{50} \ – \sqrt{8} + \sqrt{18} \\ &=& 5 \sqrt{2} -2 \sqrt{2} +3 \sqrt{2} \\ &=& 6 \sqrt{2} \end{eqnarray}
以前の記事(中1「正負の数」② 乗除・累乗)でも書きましたが、計算力の高い人ほどよく出る数は覚えてしまっているものです。
「やり方はわかるんだけど、テスト時間内に最後まで解き終わらない」という生徒ほど、参考にしてください。
>Amazonプライム・ビデオ「イミテーション・ゲーム/エニグマと天才数学者の秘密(字幕版)」
まとめ

素数とは、1および自分自身でしか割れない自然数。
素因数分解とは、自然数を素数の積の形にすること。
素因数分解のやり方は、わり算の筆算みたいに素数で割っていく。
ここで大事なコツ:37までの素数は覚えてしまう!

平方根のかけ算・わり算は、ルートの中身をかけ算・わり算。
かけ算の逆がルートを簡単にする計算。素因数分解(の筆算)を使う。
つまりは、1ペアをできるだけたくさん作ってルートの外に出してやればいい。
ここで大事なコツ:\(\sqrt{50}\) までの簡単にできる平方根も覚えてしまう!
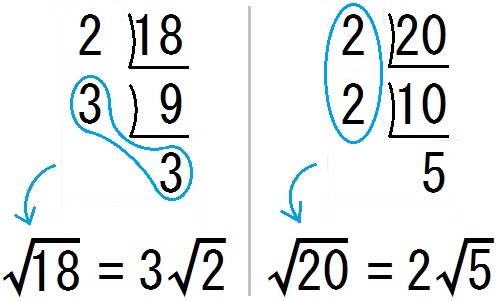
以上、素因数分解とルートを簡単にする計算でした。
次回は平方根の計算(有理化・加減乗除・展開)を一気に解説します。
ルートを簡単にすることがパッとできるなら、平方根のもろもろの計算はラクチンです。
NEXT→中学数学「平方根」のコツ④ 有理化・加減乗除・展開
[平方根の記事 一覧]
- 中学数学「平方根」のコツ① 平方根とは/平方根の大小
- 中学数学「平方根」のコツ② 有理数と無理数/循環小数と分数
- 中学数学「平方根」のコツ③ 素因数分解/ルートを簡単にする計算
- 中3数学「平方根」のコツ④ 有理化/加減乗除/展開
- 中3数学「平方根」のコツ⑤ 平方根の利用・応用問題




コメント