中学数学のつまずき解消をめざすこの連載。
中1の6単元目は「平面図形」です。
「作図の応用問題になるとわからない」
「回転移動がいまいち理解できない」
「おうぎ形問題の解き方がさっぱり…」
こうなる原因と解決法を提案していきます。
*数学の他の単元はまとめページから
まずこれから3回に分けて、作図の「わからない・できない」を解決していきます。
最終的なゴールは、直近の公立高校入試の作図問題がすべて解けるようになること。
2019年度は47都道府県中30以上で作図が出題されました。
これら実際の過去問をふんだんに使って、作図の基本から応用まで解説していきます。
作図問題でつまずく原因

中学生が作図問題でつまずく原因は以下の3つです。
- それぞれの作図の特徴を知らない
- それぞれの作図の応用範囲が整理できていない
- はじめに完成形をイメージしていない
それぞれの作図の特徴
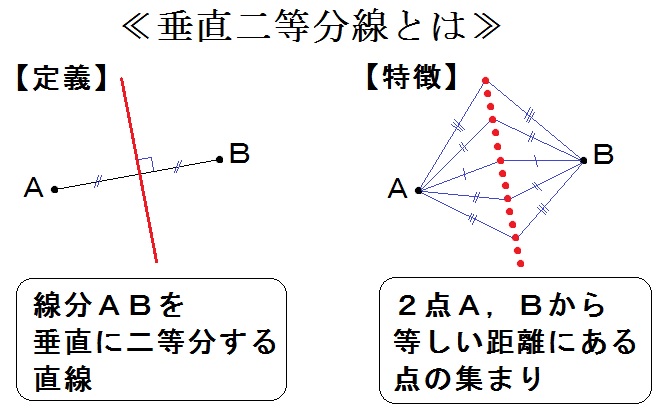
たとえば「垂直二等分線」とは
線分を垂直に二等分する直線【定義】
ということは知ってますね。
では、
2点から等しい距離にある点の集まり【特徴】
という特徴はちゃんと頭に入ってますか?
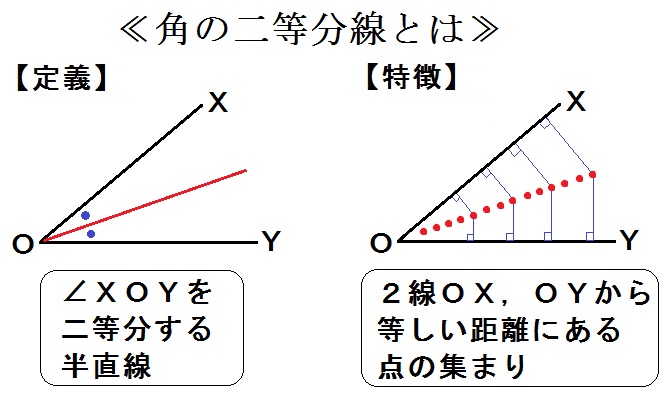
また「角の二等分線」とは
角を二等分する半直線【定義】
だとは知ってますね。
では、
2線から等しい距離にある点の集まり【特徴】
という特徴は、つねに覚えていますか?
これらの特徴もちゃんと理解して使えるようにすること。
これが、作図問題をできるようにするコツのひとつです。
応用範囲を整理する
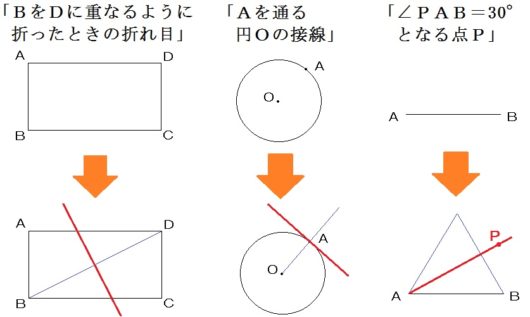
たとえば「点どうしが重なるときの折り目」と言われたら。
⇒垂直二等分線だ!
たとえば「円の接線を作図せよ」と出されたら。
⇒垂線だ!
たとえば「30°になるような直線」とあったら。
⇒正三角形&角の二等分線だ!
こんなパターンが、頭のなかで整理されていますか?
作図のできる中学生というのは、基本から難問までいろんな問題を解くうちに、こうした各作図の応用範囲が頭に入っています。
つまり、「こうきたらこう!」という脳の神経回路ができていて、どんな作図問題に出合ってもちゃんと知識を引き出してこれるんです。
それぞれの作図の応用範囲を整理すること。
これが、作図のコツのふたつめになります。
完成形をイメージする
作図のコツの最後は、問題文を読んでまず完成形をイメージすることです。
例として、福井県の公立高校入試問題を紹介します。
そこそこの難問ですね。
書き方がすぐにはわかりません。
でも、作図のできる中学生というのは完成形をまずイメージします。
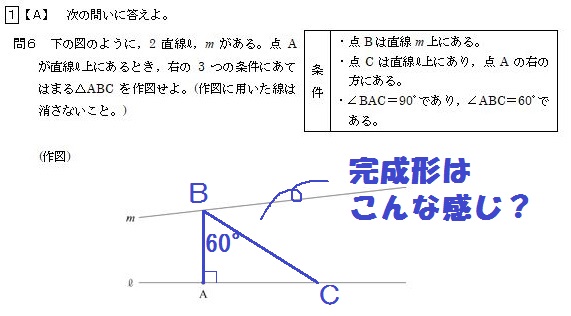
この完成形を描くにはどうしたらいいか、と考えるわけです。
(この問題の解き方は平面図形③で解説しています)
以上、
- それぞれの作図の特徴を知らない
- それぞれの作図の応用範囲が整理できていない
- はじめに完成形をイメージしていない
という3つを、以下ですべて解決していきます。
具体的には、各作図の定義と特徴それぞれがどんな応用範囲をもつのか、ぜんぶ紹介します。
そして実際の問題を解くときには、完成形をイメージしてからはじめます。
まずは垂直二等分線。
定規とコンパスの準備ができたら、いきましょー。
[中学数学「平面図形」の記事一覧]
- 垂直二等分線を使った作図
- 角の二等分線、垂線、正三角形を使った作図
- 高校入試問題を解いてみよう
- 図形の移動
- 円とおうぎ形
>Amazonプライム・ビデオで「古代びっくりトップ10(字幕版)」を観る
垂直二等分線の定義
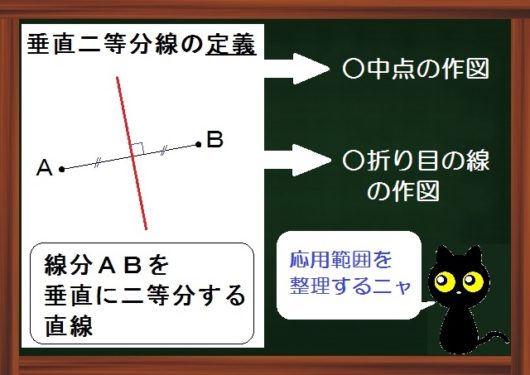
垂直二等分線の定義は
線分を垂直に二等分する直線。
つまり、ある線分をちょうど半分にまっすぐ分ける直線です。
この定義から、
- 中点(まんなかの点)の作図
- 点どうしが重なるときの折り目の作図
という2つの応用範囲が出てきます。
応用1:中点
たとえばこの山梨の入試問題。
まず完成形をイメージすると、こんな感じです↓

辺BCの中点Mさえ求まれば、あとはAとMをつなぐだけですね。
んでBCの中点はどうすれば求まる?
そう、垂直二等分線を使えばいい。
よって、解き方は以下のとおり。
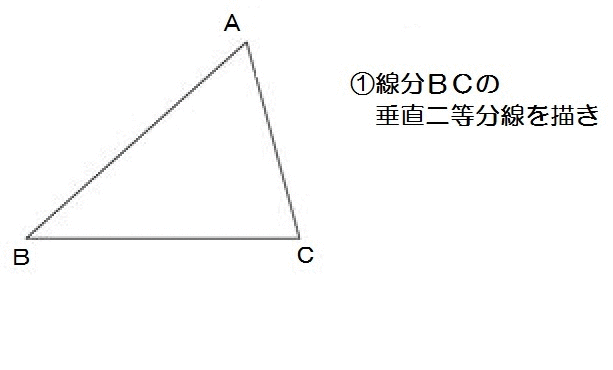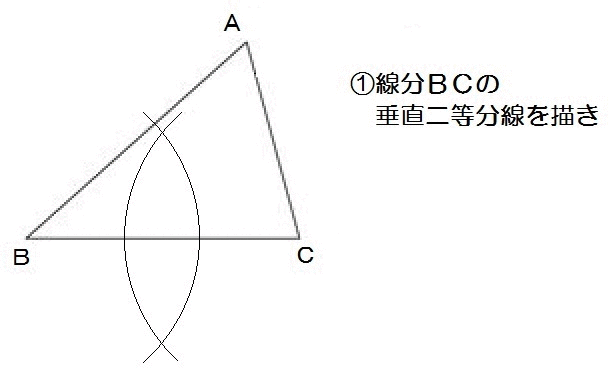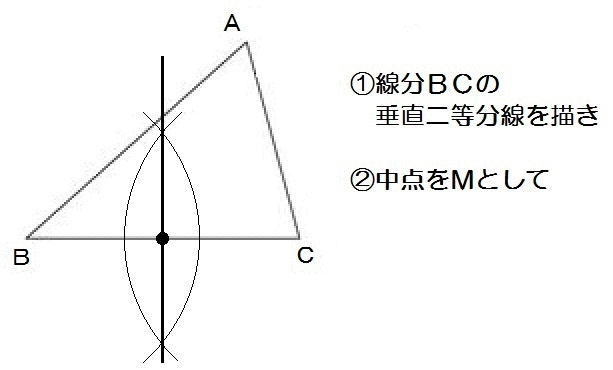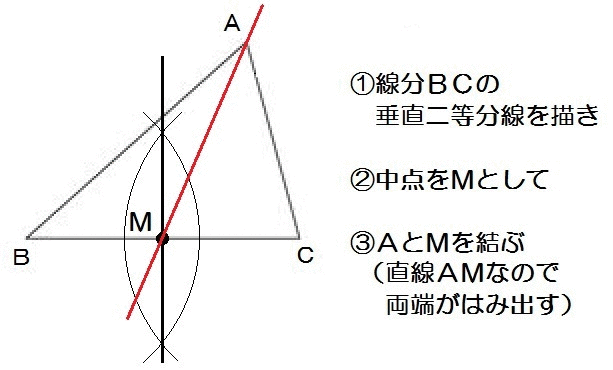
2019山梨5-1解答例
このように、線分の中点(辺のちょうどまんなか、半分の点)を求めるには、垂直二等分線が使えます。
応用2:点どうしが重なるときの折り目
つぎに、山口の入試問題から。
問題文をよく読んで、完成形をイメージすると、こんな感じですね↓
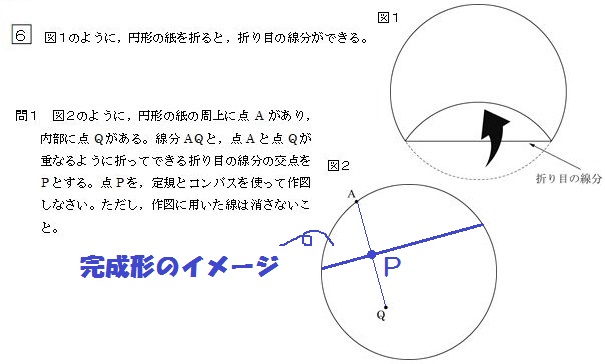
この完成形を見たら、AとQは線対称になってて、折り目の線は対称の軸になってるのがわかるはずです。
線対称とは「折って重なる」ってことだから。
んで線対称なら、「対応する頂点を結んだ線分が対称の軸によって垂直に二等分される」んでした。
つまり上の図でいうと、折り目の線は線分AQの垂直二等分線ってこと。
よって、解き方は以下のとおり。
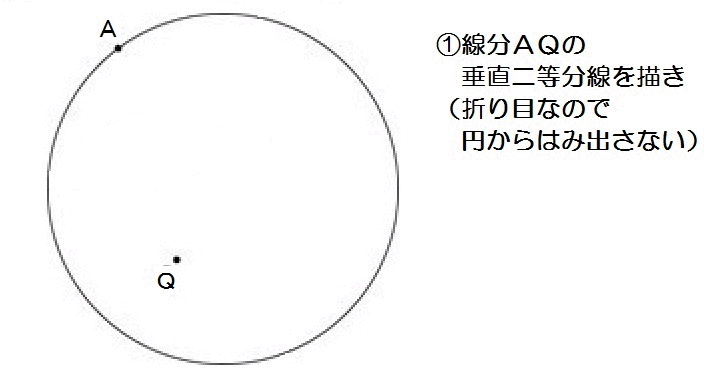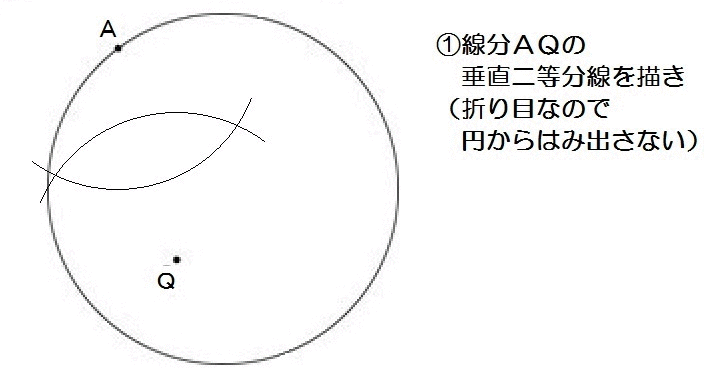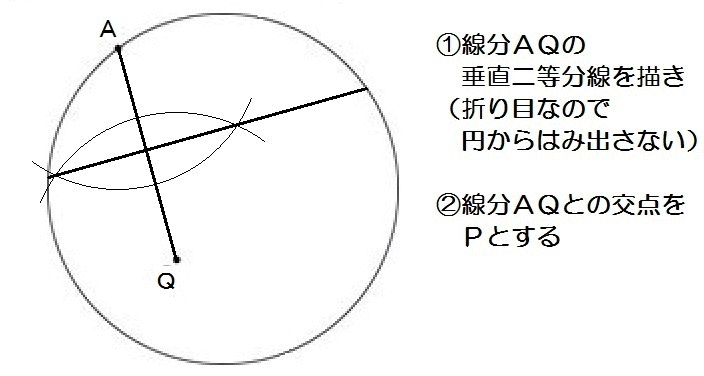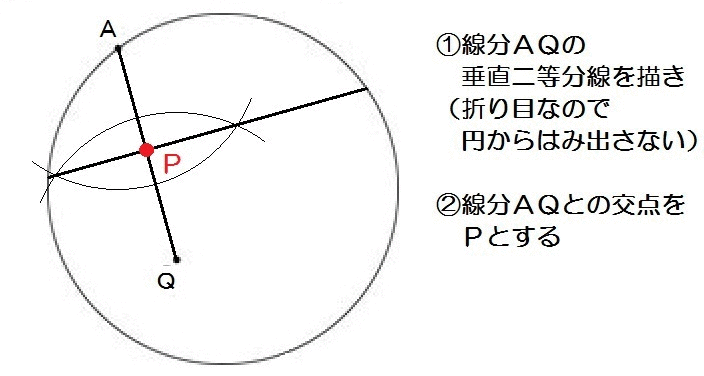
2019山口6-1解答例
このように、点どうしが重なるときの折り目の線にも、垂直二等分線が使えます。
>Amazonプライム・ビデオで「イミテーション・ゲーム/エニグマと天才数学者の秘密(字幕版)」を観る
垂直二等分線の特徴
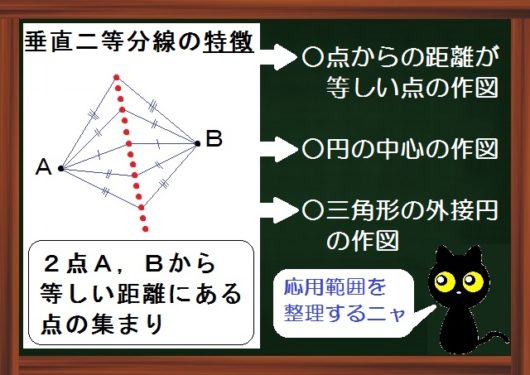
垂直二等分線の特徴は
2点から等しい距離にある点の集まり。
つまり、垂直二等分線上には、2点から等しい距離にある点が無数に並んでるってことです。
この特徴から、
- 点からの距離が等しい点の作図
- 円の中心の作図
- 三角形の外接円の作図
という3つの応用範囲が出てきます。
応用1:点からの距離が等しい
たとえばこの北海道の入試問題。
完成形のイメージはこんな感じ↓
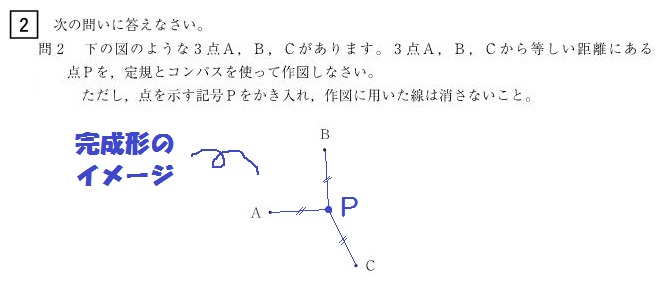
つまり、2点A,Bからの距離が等しくて、2点A,Cからの距離も等しいところを求めればいい。
じゃ、線分ABの垂直二等分線と、線分ACの垂直二等分線を描いたら、その交点がPだ。
よって、解き方は以下のとおり。
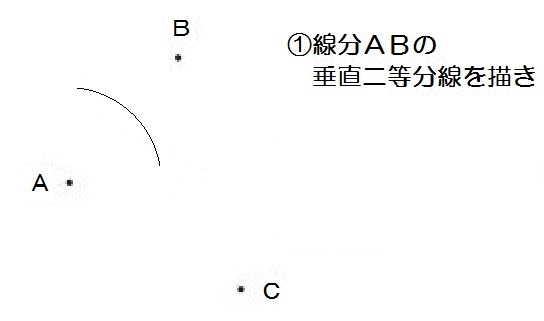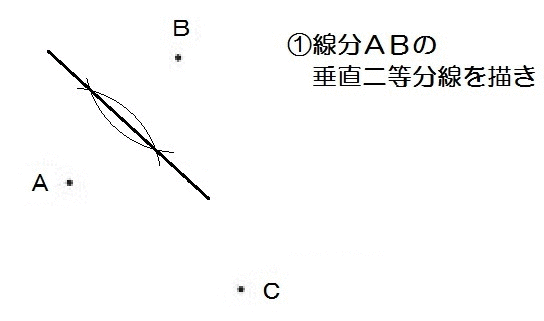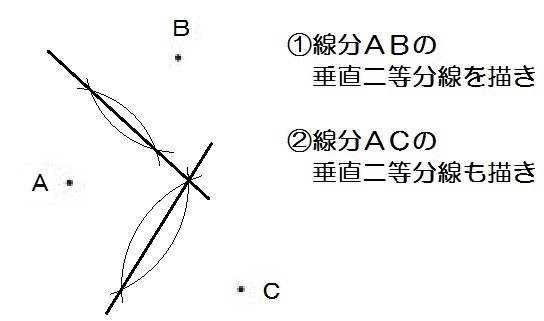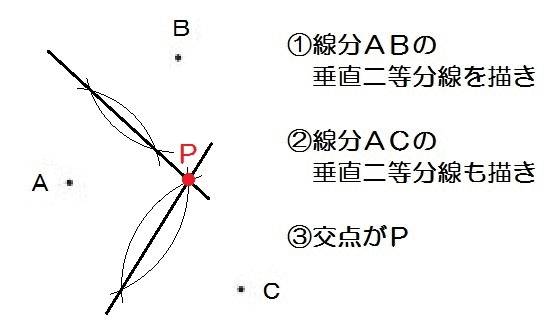
2019北海道2-2解答例
もちろん「ABとBCの垂直二等分線」「ACとBCの垂直二等分線」でやってもOKです。
好きな2組を選んでください。結果は同じです。
このように、2点から等しい距離・3点から等しい距離・4点から等しい距離…の作図に、垂直二等分線の特徴が応用できるのです。
応用2:円の中心
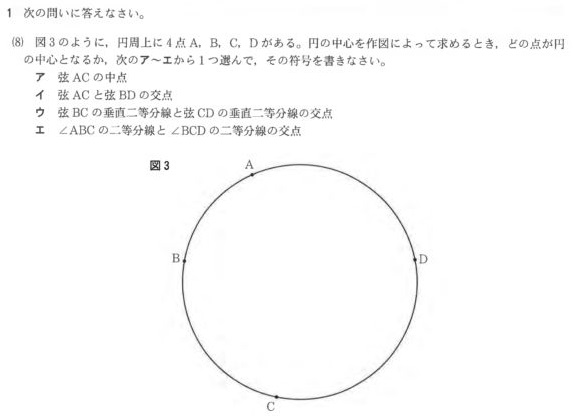
つぎに、兵庫の入試問題。
完成形はこんなイメージですね↓
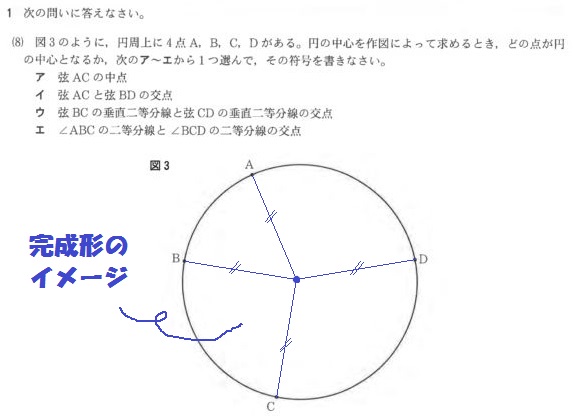
円の中心からA,B,C,Dまでの距離を書き加えてみました。
どれも等しいことがわかりますね。
円の半径ってどこでも同じ長さだから。
なので、この問題は「4点A,B,C,Dから等しい距離にある点」の作図問題と同じなんです。
よって、解き方は以下のとおり。
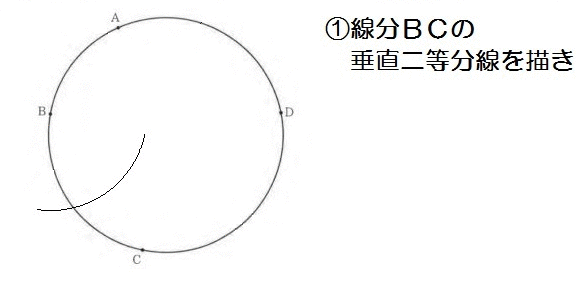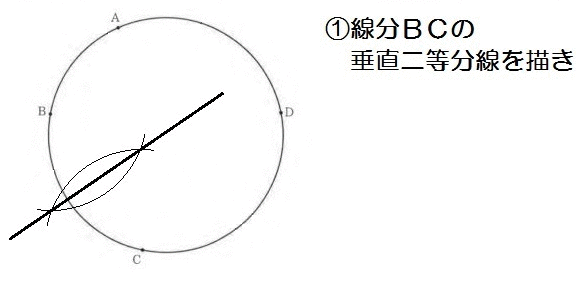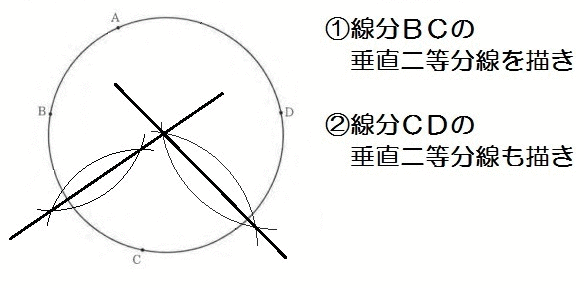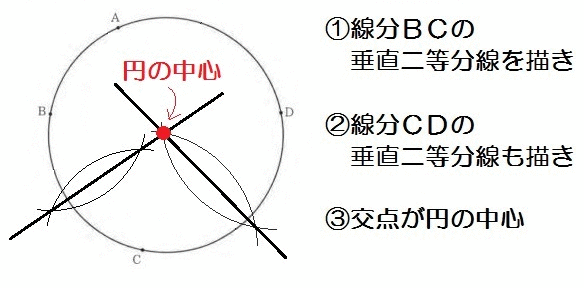
つまり答えは「ウ」になります。
このように、円の中心を求めるのにも、垂直二等分線の特徴が使えるわけです。
ちなみに「4点から等しい距離」であっても、垂直二等分線は2本あればOKです。
つまり線分ABの垂直二等分線を書く必要はありません。
だって2本あれば、交点が出るから。
つまりただ1点に定まるからです。
応用3:三角形の外接円
最後は、富山の入試問題から。
…。
もう自力で解けますね。
解答例は以下のとおり。
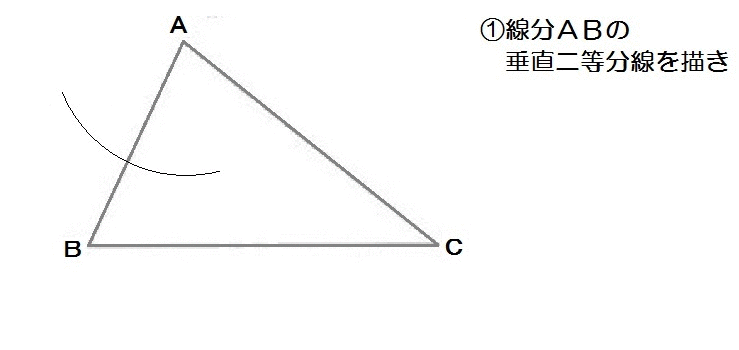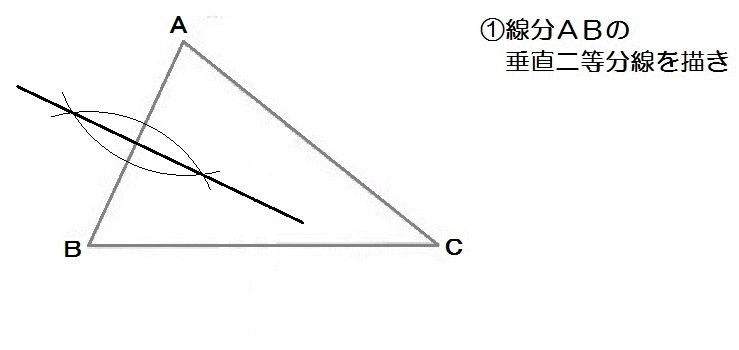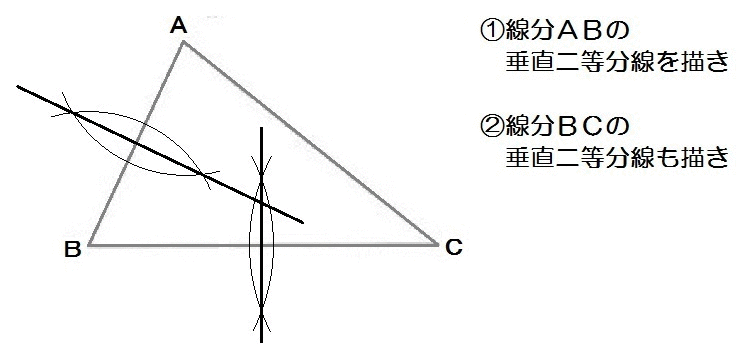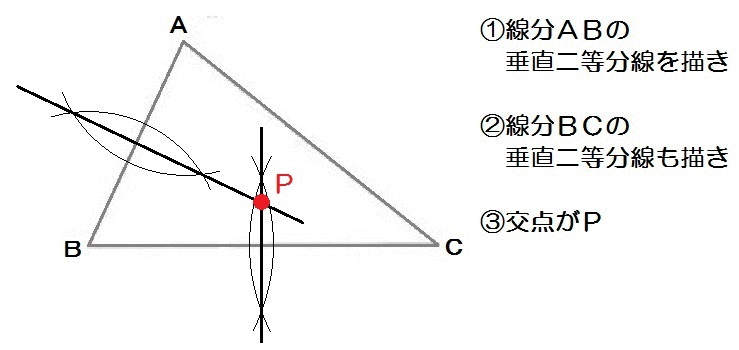
ちなみに。
この問題、点Pを中心にしてこんな円が描けます↓
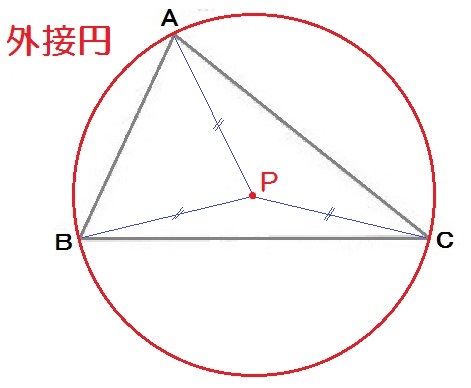
こんな三角形をぐるりと取り巻く円を「三角形の外接円」といいます。
三角形に外で接しているから、外接円という名前です。
なので、たとえば「三角形の外接円の中心を作図せよ」と、問題の聞き方が変わっても、やることは同じ。
垂直二等分線を2本描いて中心を求めましょう。
ここまでのまとめ

○中学生が作図問題でつまずく原因は3つ。
- それぞれの作図の特徴を知らない
- それぞれの作図の応用範囲が整理できていない
- はじめに完成形をイメージしていない
○だから、作図問題ができるためのコツは、
- 作図それぞれの特徴もおさえる
- 各作図の応用範囲を知って、整理する
- まず完成形をイメージしてから問題に取りかかる
○垂直二等分線の応用範囲は合わせて5つ。
定義「線分を垂直に二等分する」より、
- 中点(まんなかの点)の作図
- 点どうしが重なるときの折り目の作図
特徴「2点からの距離が等しい点の集まり」より、
- 点からの距離が等しい点の作図
- 円の中心の作図
- 三角形の外接円の作図

2019北海道2-2解答例
次回は「角の二等分線」および「垂線」の応用範囲をぜんぶ紹介します。
(ついでに「正三角形」も)
そして3回目は確認テストとして、入試問題から難問を選りすぐって解いていく予定です。
NEXT→中学数学「平面図形」のコツ② 角の二等分線・垂線を使った作図
[中学数学「平面図形」の記事一覧]
- 垂直二等分線を使った作図
- 角の二等分線、垂線、正三角形を使った作図
- 高校入試問題を解いてみよう
- 図形の移動
- 円とおうぎ形





コメント
コツの一つ、
・まず完成形をイメージしてから問題に取りかかる
はその通りだと思いますが、
そもそも、完成形をイメージできない生徒が少なくありません。
(フリーハンドで書かせると、全然違う図を書いていたり、何も書けなかったり)
完成形をイメージできるようにするには、どんなコツがありますか?
すぐにイメージできる子は少ないので、
・問題を読み上げながら完成形を描いてあげる
・もういちど、今度は自力で描かせてみる
をくりかえしてます。