連立方程式の文章題、2回目です。
今回から問題パターン別の解き方のコツを解説していきます。
まずここでは
- 分配の問題
- 整数、自然数の問題
- 平均の問題
- 過不足の問題
という4パターンについて。
道のり問題、割合の問題などは次回以降に解説します。
それぞれの問題のコツを端的に伝えるとともに、練習問題も載せますので、ここでつまずいているすべての中学生の参考にしてください。
分配問題のコツ

このような分配問題におけるコツは以下の2つです。
- 「\(x+y=\mbox{(分ける前の合計)}\)」でひとつ式が立つ
- 難しければ、分配後の数を \(x , y\) で表してから式をつくる
解き方
例1)森崎くんと安田くんで20本の牛乳を分けあったら、安田くんの牛乳の本数は森崎くんの牛乳の本数の2倍より2本多かった。それぞれの牛乳の本数を求めよ。
まず「森崎くんの牛乳を \(x\) 本、安田くんの牛乳を \(y\) 本とする。」と書きます。
次に連立方程式を立てていきますが、「20本の牛乳を分けあった」とあるので、
$$ x+y=20 $$
これはすぐに立てられる。
あとは後半の「安田くんの牛乳の本数は森崎くんの牛乳の本数の2倍より2本多かった」という文に沿って、
$$ y=2x+2 $$
とすれば、連立方程式が完成です。
このように、分配の問題では「\(x+y=\mbox{(分ける前の合計)}\)」でまずひとつ式をつくる。
これがコツのひとつになります。
(ちなみに答えは森崎くん6本、安田くん14本)
例2)鈴井くんと大泉くんは合わせて68枚の絵ハガキを持っている。鈴井くんが大泉くんに5枚渡したら、鈴井くんの枚数は大泉くんの枚数のちょうど3倍になった。鈴井くん、大泉くんがはじめに持っていた絵ハガキの枚数をそれぞれ求めよ。
例題2も同じです。
まず「鈴井くん、大泉くんがはじめに持っていた絵ハガキの枚数をそれぞれ \(x\) 枚、\(y\) 枚とする。」等と書いたら、
$$ x+y=68 $$
これは簡単にできますね。
難しいのは後半です。
そこで「鈴井くんが大泉くんに5枚渡した」後の枚数を、\(x , y\) を使って表してみましょう。
- 鈴井:\(x-5\) 枚
- 大泉:\(y+5\) 枚
この2つの関係が「鈴井くんの枚数は大泉くんの枚数のちょうど3倍」なんです。
$$ x-5=3(y+5) $$
と、もうひとつの式も立てられるはずです。
このように、分配後の数を \(x , y\) で表してから式をつくる。
これが立式が難しい場合のもうひとつのコツになります。
(ちなみに答えは鈴井くん56枚、大泉くん12枚)
練習問題
以上のコツは中1の「1次方程式文章題」でも詳しく解説しています。
あわせてご参考ください。
→中学数学「1次方程式」文章題の解き方②【分配、年齢、貯金】
では、練習問題を2つ載せます。
ぜひチャレンジしてみてください。
解答は末尾に記載、質問はコメント欄からどうぞ。
問1)大人と子供あわせて50人にアメを配る。大人には3個ずつ、子供には2個ずつ配ると、配ったアメは全部で138個になった。大人と子供の人数をそれぞれ求めよ。
問2)戸次くんと音尾くんの二人で15本の団子を分けた。皿に分け終えたあとに、戸次くんが音尾くんの団子を3本取ったので、戸次くんの団子の本数は音尾くんの団子の本数の3倍より1本少なくなった。はじめに皿に分けたときの、二人の団子の本数をそれぞれ求めよ。
問1)大人38人、子供12人 問2)戸次くん8本、音尾くん7本
>Amazonプライム・ビデオで「昼のセント酒」(戸次重幸主演)を観る
整数、自然数問題のコツ

このような整数・自然数問題のコツも2つです。
- (わられる数)=(わる数)×(商)+(余り)
- 「○△」という2桁の自然数の表し方は「10×○ +△」
解き方
例3)大小2つの整数があり、その和は51である。また、大きい数を小さい数でわると商が6で余りが2になる。この2つの整数を求めよ。
まず「大きい数を \(x\) 、小さい数を \(y\) とする。」等と書く。
「その和は51」とあるので、
$$ x+y=51 $$
ここまではいいですね。
問題は後半。
ここで多くの中学生が以下のようにしてしまいがちです。
$$ x \div y =6 \mbox{…2}$$
こんなふうに「…」があっては、連立方程式を解くことができません。
だから、正しくはこう立てます。
$$ x=6y+2 $$
(わられる数)=(わる数)×(商)+(余り)
この関係を使ってわり算を表すというのが、整数・自然数問題のコツのひとつです。
(ちなみに答えは大44、小7)
例4)2桁の自然数がある。一の位の数は十の位の数の2倍より1大きく、十の位の数と一の位の数を入れかえてできる数は、もとの数の2倍より4小さい。もとの自然数を求めよ。
また、このような2桁の自然数の問題では、「十の位の数を \(x\) 、一の位の数を \(y\) とする。」等とはじめに書きます。
なぜ各位の数字をわけて考えるのか?
こうすれば、この2桁の自然数が「\(10x+y\)」と表せるからです。
たとえば「42円」って、十円玉4枚+一円玉2枚ですね。
だから \(42=10 \times 4 + 2\) と表せる、これと同じことです。
ついでに「24円」は、十の位と一の位を入れかえているから \(10 \times 2 + 4\) 。
じゃあ……、もうわかりますね。
\begin{eqnarray} \left\{ \begin{array}{l} y=2x+1 \\ 10y+x =2(10x+y)-4 \end{array} \right.\end{eqnarray}
これが例題4の連立方程式になります。
以上のように、「○△」という2桁の自然数の表し方は「10×○ +△」、これが整数・自然数問題のもうひとつのコツになります。
(ちなみに答えは49)
練習問題
ついでに、3桁の自然数も4桁の自然数も同じ考え方でいけます。
「○△□」という3桁の自然数ならば「100×○ + 10×△ + □」です。
簡単ですね。
以上のコツも中1数学の以下の記事で詳しく解説しています。
あわせてご参考ください。
では、練習問題です。
解答は末尾に記載、質問はコメント欄からどうぞ。
問3)大小2つの整数がある。大きい数の2倍は小さい数の7倍より3小さく、大きい数の3倍を小さい数でわると商は9で余りは6になるという。この2つの整数を求めよ。
問4)十の位が8である3桁の自然数がある。各位の数の和は、百の位の数の6倍になる。また、百の位の数と一の位の数を入れかえた数は、もとの数より396大きい。もとの自然数を求めよ。
問3)大23、小7 問4)387
平均問題のコツ

このような平均問題のコツもやはり、2つあります。
- 平均の公式を2種類とも使いこなす
- クラスの平均点問題は表を書いて整理する
解き方
例5)36人のクラスで英語のテストをしたところ、男子の平均点は80点、女子の平均点は71点、クラス全体の平均点は75点になった。このクラスの男女の人数をそれぞれ求めよ。
「男子を \(x\) 人、女子を \(y\) 人とする。」等とします。
クラスの人数は合わせて36人なので、
$$ x+y=36 $$
ひとつはすぐ立式できますね。
ここからもうひとつ式をつくるときに、2つのコツが効いてきます。
まず平均の公式、2種類とも覚えていますか?
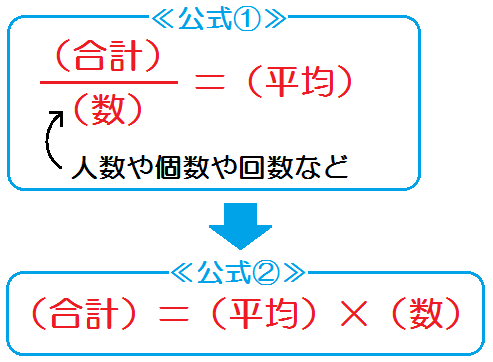
平均の公式
特に公式②を忘れている生徒が多い。
公式②を使えば、たとえば
- 男子の合計点:\(80x\)
- 女子の合計点:\(71y\)
- クラス全体の合計点:\(75 \times 36\)
と表せます。
よって、(男子の合計点)+(女子の合計点)=(クラス全体の合計点)なので
$$ 80x+71y=75 \times 36 $$
と、もうひとつの式をつくることができます。
でも中には「クラスの平均点問題はごちゃごちゃしてて頭の中が整理できない」という中学生もいるでしょう。
そんな人にはもうひとつのコツ、表を書いて整理することをおススメします。
解答用紙の余白に、3列×2行のこんな表を書いてみましょう↓
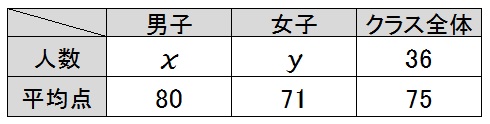
問題が整理できるはずです。
あとはこの表から、上述の式を立ててもいいし、あるいは公式①を使って
$$ \frac{80x+71y}{36} =75 $$
と作ってもいい。両辺に36をかけたら同じ式となります。
このように、平均の公式を2種類とも使いこなす、そして難しければ表を書いて整理する。
これが平均問題のコツになります。
(ちなみに答えは男子16人、女子20人)
練習問題
以上のコツもやはり、中1「1次方程式文章題」で詳しく解説しています。
あわせてご参考ください。
では、連立方程式文章題の平均にかんする練習問題です。
解答は末尾、質問はコメント欄からどうぞ。
問5)男子18人、女子12人のクラスで数学のテストをしたら、クラス全体の平均点は67点で、女子の平均点が男子の平均点より5点高かった。男女の平均点をそれぞれ求めよ。
問5)男子65点、女子70点
過不足問題のコツ

最後に、このような過不足問題のコツ。
連立方程式においてはたったひとつです。
- 横棒グラフを描いてイメージする
解き方
例6)2000円を持ってお菓子を買いに行ったところ、ポテチ12個とキャンディ7個を買おうとすると120円不足し、ポテチ7個とキャンディ12個を買うと130円余ることがわかった。このポテチとキャンディの単価はそれぞれいくらか求めよ。
まず「ポテチの単価 \(x\) 円、キャンディの単価 \(y\) 円とする。」等と書きます。
次に連立方程式を作りますが、ここで「120円不足だから-120だ」「130円余るから+130だ」と安易に考えて
\begin{eqnarray} \left\{ \begin{array}{l} 12x+7y=2000-120 \\ 7x+12y=2000+130 \end{array} \right.\end{eqnarray}
としたら間違いです。
理由は、下の図を見ればわかります。
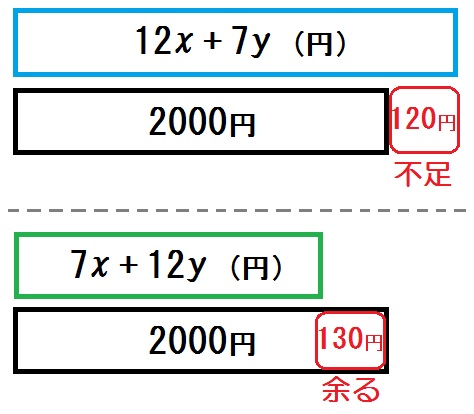
このように横棒グラフのような図を描いてみれば、正しくは
\begin{eqnarray} \left\{ \begin{array}{l} 12x+7y=2000+120 \\ 7x+12y=2000-130 \end{array} \right.\end{eqnarray}
だというのがわかります。
過不足問題において、「不足」や「余る」という言葉の意味にいつもとまどう。
そんな中学生は横棒グラフを描いてイメージするといいでしょう。
(ちなみに答えはポテチ130円、キャンディ80円)
練習問題
以上のコツもすでに、中1「1次方程式文章題」で詳しく解説しています。
あわせてご参考ください。
棒グラフについては記事の中ほどに載っています。
それでは、最後の練習問題です。
連立方程式文章題における過不足問題、ぜひチャレンジしてみてください。
解答は末尾、質問はコメント欄からどうぞ。
問6)1500円を持ってマクドナルドに行った。てりやきバーガーとチキンフィレオを2個ずつ買うと100円余るが、てりやきバーガーを3個、チキンフィレオを2個にすると240円足りない。てりやきバーガーとチキンフィレオの単価をそれぞれ求めよ。
問6)てりやきバーガー340円、チキンフィレオ360円
>Amazonプライム・ビデオで「ファウンダー ハンバーガー帝国のヒミツ」を観る
まとめ

連立方程式の文章題、問題パターン別のコツ。
○分配の問題は
- 「\(x+y=\mbox{(分ける前の合計)}\)」でひとつ式が立つ
- 難しければ、分配後の数を \(x , y\) で表してから式をつくる
○整数、自然数の問題は
- (わられる数)=(わる数)×(商)+(余り)
- 「○△」という2桁の自然数の表し方は「10×○ +△」
○平均の問題は
- 平均の公式を2種類とも使いこなす
- クラスの平均点問題は表を書いて整理する
○過不足の問題は
- 横棒グラフを描いてイメージする
次回は「速さ・時間・道のり」問題のコツをお伝えします。
連立方程式文章題において、もっとも多くの中学生が難しく感じるところ。
また模試でも入試でも必ずといっていいほど頻出するところ。
その道のり問題を「わかる・できる」ようにするためのコツです。
お見逃しなく。








コメント
問5の式を教えて下さい。
学習塾オープンおめでとうございます。
近くにあれば、わが子を通わせたいくらいです。
きっとすばらしい塾になることでしょう。
益々のご活躍をお祈りしております。
(連立方程式とは関係ないことで失礼いたしました。)
嬉しいお言葉ありがとうございます。
開校準備でほとんどコメントも読めていませんがまた落ち着けば細々とこちらのブログも更新していきます。
いつも参考にしております。
また以前一次方程式の質問を答えて頂きありがとうございます。
再度の質問で申し訳ないですが
問4の途中式を教えて頂きたいです。
よろしくお願いいたします。
>す様
遅くなりました。
問4)百の位をx、一の位をyとする。
x+8+y=6x・・・①
100y+80+x=(100x+80+y)+396・・・②
両方を整理して
y=5x-8・・・①’
-x+y=4・・・②’
たとえば、①’を②’に代入して
-x+(5x-8)=4
解いて、x=3・・・③
③を①’に代入して、y=7
大変参考になる記事で、役に立っています。ありがとうございます。
解答を見たいのですが、「解答は一行下をドラック反転」が何を意味するのかわかりません。どういうことでしょう?
グレーボックス内の一番下の空白部分をマウスあるいは指でドラッグすると、文字の色が反転して解答が現れる、ということです。
ただiPhoneなどでは見れないみたいで、ぜんぶ修正したつもりが連立方程式文章題の記事だけ未修正でしたm(_ _)m
数日内に、なおします。