こんにちは、重悟(ジュウゴ)です。
中学1年のとき数学で「絶対値」を習って、おもわず「はあっ!?」と叫んだことがあります。
「絶対値とは数直線上における原点Oからの距離である」
「|x|は x≥0のとき x、x<0のとき -x」
・・・
何をいきなり言い出してんの?
それってあとでどんなふうに使うの?
そんな疑問を抱えたまま大人になってしまいました。

そこでいま、あのころの自分にむけて、
「絶対値ってそもそも、こんなふうにして生まれた考え方なんだ。こんな分野で使われているんだ」と解説することにしました。
[関連記事]
絶対値とは「点からの距離」のこと

まず、絶対値とはそもそも何かという話から。
絶対値を簡単にいうと、「点からの距離」のことです。
たとえば競走で説明しましょう。
絶対値とは距離の大きさだけのこと(方向はムシ)
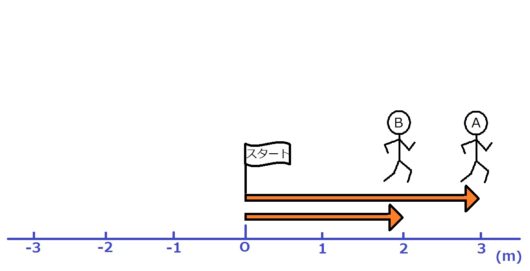
図1
まず、AくんとBくんの2人が「おなじ方向に」走って競走するとします。
すると数秒後、図のようにAくんがちょびっとリードしたとします。
このとき、下にひいた目盛り(じっさいは巻尺とか)を読むと、
Aくん:3m
Bくん:2m
ですね。だから、スタート地点という点からの距離、つまり絶対値は、
Aくん:3
Bくん:2
となります。これはまあええわな。
(ちなみにめんどうだから絶対値の単位はぬきとします。)
つぎに、「反対方向に走ってもいい」という競走とします。
んなアホなとかいわずに、そんな競走があってもオモロイじゃないですか。
図にするとこんなかんじ↓
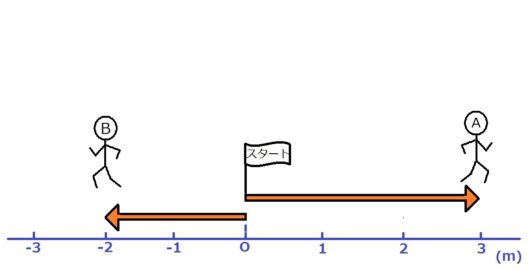
図2
これ、下の目盛を読んだら、
Aくん:3m
Bくん:-2m
となります。
「じゃあBくんは走れば走るほどマイナスになるんか?そんなん、走る前からAくんの勝ちやん」とはならないですよね。
だって、Bくんだって走った距離は「2m」だから。
つまりスタート地点からの距離(絶対値)は、
Aくん:3
Bくん:2
となるわけです。
これが、
-2の絶対値は2(数学記号でいうと |-2|=2 )
という理由なんです。
絶対値とは、方向をかんぜんに無視して、点からの距離(長さ、大きさといってもいい)だけを表す値のことなんですね。
それでなんの意味があるわけ?
ただここまでは中学のぼくでも理解していました。
「ようするにマイナスとかの符号を取ればいいんでしょ。そんなのカンタン。わからないのは、そんなことするのになんの意味があるかってこと」
ここなんです、絶対値という考え方のわかりにくいところは。
そこで、さっきの競走の例をもういちど使います。
今度は「空を飛んでもいい」という競走にします。図にするとこんなかんじ。
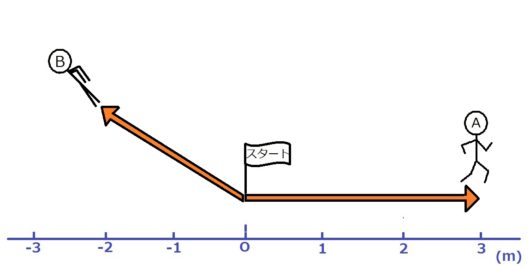
図3
「はあ?」とか言わずにもうちょっと付き合ってください。
さて、スタート地点からの距離は、つまり絶対値は、AくんとBくん、どちらのほうが大きいでしょうか?

これ、Bくんの矢印の長さがわからないですよね。ななめに飛んでいってるわけですから。
つまり、「3と-2ではどちらの絶対値が大きいか」という単純な問題じゃなくなるわけです。
この場合、縦軸にもうひとつ目盛をつけると、Bくんの絶対値は計算で求めることができるようになります。
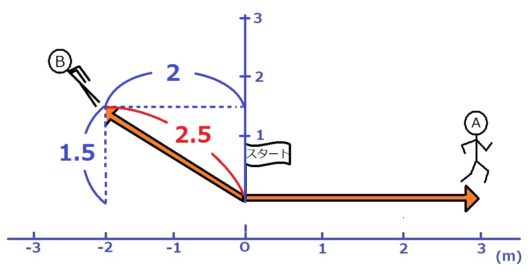
図4
中3で習う「三平方の定理(ピタゴラスの定理)」を使えばいいんです。
横の長さが2、たての長さが1.5だから、もとめる矢印の長さは
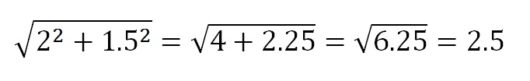
と出てきます。これで
Aくん:3
Bくん:2.5
と2人の絶対値(スタート地点からの距離)をくらべることができ、「Bくんは空を飛んでもやっぱりAくんより遅いんだな」ということがわかります。

ここで、Bくんの矢印が左側、つまりマイナス側に伸びていることに注目してください。
つまり数学的にいうと、Bくんの矢印は「マイナス」なんです。図2とおなじように。
でも、Bくんの飛んだ距離は「マイナス」なんかじゃないですよね。
そこで、「方向は無視して、その距離(長さや大きさ)だけをくらべるときには、マイナスは無しってことにしよう。そんで『マイナスは無しよ』という記号もほしいな、そうだ、| |という記号にしよう」
ということで、絶対値という考え方が生まれたんですね。
19世紀のことだったそうです。
>Amazonプライム・ビデオで「プレステージ (字幕版)」を観る
絶対値は複素数平面から生まれた

このように、絶対値という考え方は、数直線にもうひとつ縦軸をつけて、いわゆる「座標平面」となったときにはじめて活きてきます。
数直線だけだったら別に必要ないでしょう。だって、符号をとるだけで原点からの距離になるんだから。(-2の絶対値が2のように)
ななめの矢印が出てきて、「どっちの矢印が長いの?」とくらべるときにはじめて、絶対値(原点からの距離)という考え方が必要になるんです。
複素数平面ってどんなもの?
この「どっちの矢印が長いの?」とくらべる必要が出てきたのは、19世紀に「複素数平面」という数学分野が誕生してからです。
高校の数Ⅲで、最初に習う単元ですね。電気工学、機械工学、3D設計などの仕事には必須の知識です。
複素数については別の記事でくわしく書きますが、ようするに実数にくわえて虚数というなんだかよくわからない数まで含めちゃったものをいいます。
そんで複素数平面では、横軸に実数の目盛を、たて軸に虚数の目盛をつけて、複素数を平面上に描いちゃうわけです。
たとえばこんなかんじ。
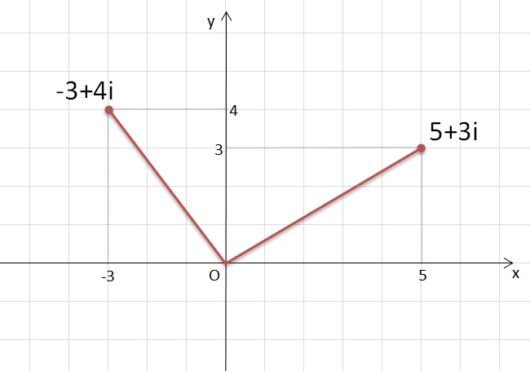
関数のグラフで出てきた「座標平面」とまったく同じですね。
そして、さっき見た「Bくんが飛んでる図」と似てますね。つまりななめ線が出てきますね。
この2本の赤線の長さをくらべたりするのに、絶対値が必要なんです。
ためしに左右両方の赤線の長さを求めてみます。
やっぱり三平方の定理(ピタゴラスの定理)を使います。
右(5+3i):![]()
左(-3+4i):![]()
ってことで、右のほうが長いとわかります。
複素数平面における線の長さこそ、絶対値の本当の意味
じつは、こうした使い方こそが絶対値の本来の、そもそもの使い方なんです。
つまり、5+3iという複素数の√34、または-3+4iという複素数の5にあたる値こそ、絶対値の本当の意味なんです。
これ、19世紀にワイエルシュトラウスというドイツの数学者が言い出しました。
ワイエルシュトラウスによる定義は以下のとおりです。

ここでワイエルちゃんがたまたま縦棒2本という記号を思いついたので、いまでもぼくたちはワイちゃんの思いつきに従っているわけです。
ちなみに数学の記号なんてほとんどみんな、発案者の思いつきです。
またどこかで「数学の記号の歴史」と題してまとめますね。
まあとにかく、
なぜ絶対値なんてものを習うのかといったら、それは複素数平面という分野からきているというお話でした。
たださ、複素数平面を習うのって高2、高3だよ?
中1でいきなり絶対値って、早くね?もっとあとでもよくね?
絶対値は他の分野でも使われる
ただ、絶対値はほかの数学分野でも使われております。
ようするに、座標平面上でななめ線が出てきてその距離を求めよ、なんて問題には絶対値が必要になってくるわけです。
たとえば高校の数Ⅱで出てくる「点と直線の距離」。
証明は省きますが、定理だけ書きだすとこんなかんじ。
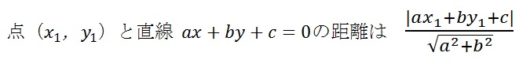
分子に絶対値が出てきます。
またおなじく数Ⅱで出てくる「領域」。
たとえば「不等式 y≧|x-1| の表す領域を図示せよ」なんて問題が出てきます。
んで、これを解くための準備として、数Ⅰの最初のほうで「不等式 5≧|x-1| を解け」なんて問題が出されるわけです。
こうみてくると、高1からけっこうがっつり絶対値を使うってことですね。
にしても、中1は早くね?
まとめ
以上、絶対値とは何か?それにどんな意味があるのか?という疑問をみてきました。
まとめると、
- 絶対値とは点(原点)からの距離。方向とか考えない。
- 数直線だけみていても、絶対値には意味がない。
- たて軸も加えて「座標平面」となったときに、はじめて絶対値を使う意味が出てくる。
- とくに複素数平面でよく使う。
- 絶対値という考え方が生まれたのも、複素数平面という分野が誕生した19世紀。
- 定義と記号を考えたのは、ドイツの数学者ワイエルシュトラウスという人。
- 中1で絶対値を習うのは、高校数学のための準備。(早くね?)
最後に、なぜ「絶対値(absolute value)」という名前なのか、いろいろ調べてみましたが、わかりませんでした。
どなたか知っている人がいたら教えてください。





コメント
≪…絶対値とは点(原点)からの距離…≫を、数の言葉ヒフミヨ(1234)の『幻のマスキングテープ』の『刀札』模様で、自然数の進む方向が分かる【ヒ フ ミ ヨ イ ム ナ ヤ コ ト】の[ものさし]がある。
この[ものさし]は、[表][裏]があるが、透明な[ものさし]なら同じモノである。 数え始める方向を示す[ものさし]です。
10までの『刀札』のジグザグの始まりの向きが、数直線点[0]から右へ進むか左へ進むかを決める。
この[ものさし]は、右に進んだ時の素数と左に進んだ時の素数でジグザグ模様が完成する。
この物語の淵源は、2冊の絵本で・・・
すうがくでせかいをみるの
もろはのつるぎ (有田川町ウエブライブラリー)
≪…方向とか考えない…≫は、数の言葉ヒフミヨ(1234)の[直交座標][極座標]での振る舞いととりたい・・・
≪…複素数平面における線の長さこそ、絶対値の本当の意味…≫を、数の言葉ヒフミヨ(1234)が、平面(2次元)からの送りモノとして眺めるとコトに観える・・・
[…] 参考 絶対値とは何か?なんの意味があるのか?簡単に解説してみた重悟のブログ […]
絶対値って、何の役に立つのか?やっと分かりました。ありがとうございました。
これで絶対値の学習を進めることができます。