三角比・三角関数について5回目の記事です。
≪連載記事一覧≫
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)
前回までで「三角比の拡張」「ラジアン」「三角関数のグラフ」について復習しおえたので、今回からいよいよフーリエ級数の中身に入っていきます。
このフーリエ級数を理解することで初めて、三角関数は何の役に立っているのかが理解できます。
文系の人にとっては「数式を見ただけでサブイボが!」ってなりますが、ジュウゴもおなじなので安心してください。
できるだけスモールステップでわかりやすく解説していきます。
逆に「フーリエ級数とか初歩中の初歩やん、フーリエ変換はやらないの?」なんて人は、ジュウゴの記事にまちがいがないか確かめてもらえると助かります。
それでは、フーリエ級数を一緒にやっつけていきましょー。
スポンサーリンク
フーリエ級数とは何か
フーリエ級数の意味
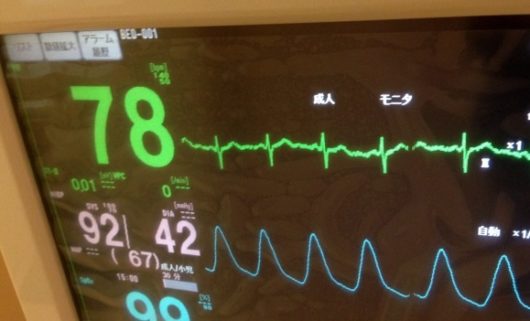
波の形というのは千差万別です。
海を眺めればよくわかりますし、心電図などの形も人によってちがいます。
また音を波で表した「音波」も、音の高さ・大きさ・音色によって波形がぜんぶちがいます。
こうしたこの世界のあらゆる波の形が
「コサインとサインの足し算だけですべて表せる」
というのがフーリエ級数です。
厳密にいうと「ほとんどすべて」なんですが、実用上は「すべて」と思っていいでしょう。
これは驚くべきことなんです。
音を例にとるとよくわかります。
だって、音叉をたたいた単純な音も、オーケストラの演奏も、街並みの喧騒も、恋人の話し声も、すべてコサインとサインの足し算に分解できるってことですから。
逆にいえば、コサインとサインをうまいぐあいに足し合わせてつくった音と、オーケストラの生演奏とは、まったくおなじに聞こえるのです。
ちなみにこれが「録音」の原理でもあるんですね。

フーリエが言い出したフーリエ級数
「波は(つまり周期的な関数は)すべて、コサインとサインの足し算で表せる」。
これを初めて言い出したのが、名前のとおり、ジョセフ=フーリエというフランスの学者です。
ジョセフ=フーリエは18世紀末から19世紀にかけて活躍した学者で、ちょうどフランス革命期に青年時代をすごしました。
ナポレオンのエジプト遠征の際には従軍したりもしています。

ジョセフ=フーリエ
(wikipedia)
フーリエは1807年、熱伝導にかんする研究論文のなかではじめて、フーリエ級数を言い出しました。
「周期的な関数は(ほとんど)ぜんぶ、三角関数の和で表せる」という主張に、ラプラスやラグランジュはじめ、当時のお偉い学者たちはびっくり。
おおきな波紋をよびましたが、やがてその主張はすこしずつ認められていきます。
では、どんな波の形でもコサインとサインの足し算で表せるとはどういうことなのか、実際に見ていきましょう。
![]()
三角関数を足しあわせていくと・・・
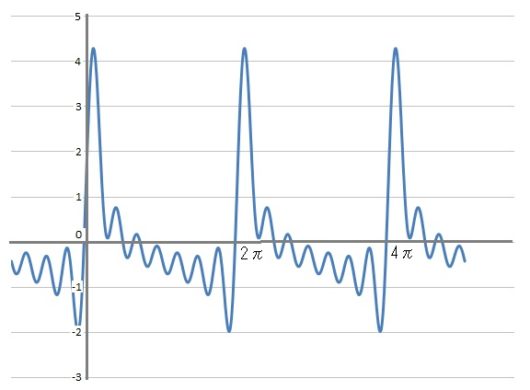
たとえばこんな波の形↑
一見ふくざつそうに見えますが、よく見ると周期的な形をしていることがわかります。
これ、14個の単純な三角関数を足し合わせただけなんです。
足し算した三角関数はこちら
以下の14個の三角関数の、右辺をぜんぶ足しただけです。
$$y = \frac{2}{3}\cos x ~~~~~~~~y = \frac{2}{3}\sin x$$
$$y = \frac{4}{9}\cos 2x ~~~~~~~y = \frac{3}{5}\sin 2x$$
$$y = \frac{8}{27}\cos 3x ~~~~~~~y = \frac{4}{7}\sin 3x$$
$$y = \frac{16}{81}\cos 4x ~~~~~~~y = \frac{5}{9}\sin 4x$$
$$y = \frac{32}{243}\cos 5x ~~~~~~~~y = \frac{6}{11}\sin 5x$$
$$y = \frac{64}{729}\cos 6x ~~~~~~~y = \frac{7}{13}\sin 6x$$
$$y = \frac{128}{2187}\cos 7x ~~~~~~~y = \frac{8}{15}\sin 7x$$
数字はジュウゴがてきとうに決めました。
ただよくみると、いくつかルールに従って決めているのがわかると思います。
その話はまた後ほど。
それぞれの三角関数のグラフ
14個それぞれのグラフは、以下のようになります。
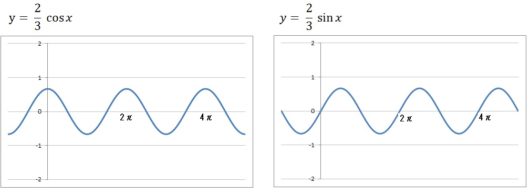
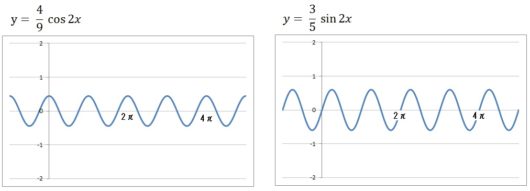
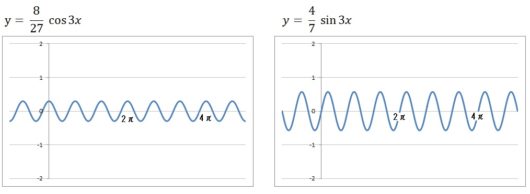
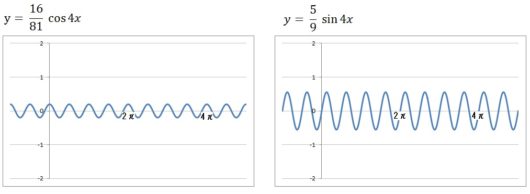
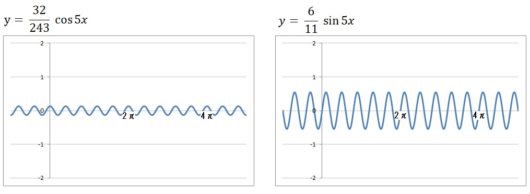
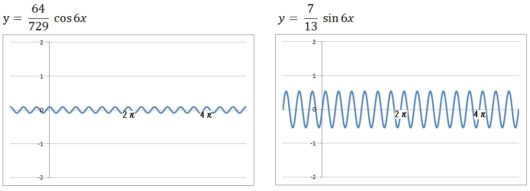
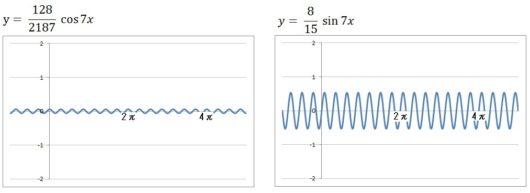
前回の記事で復習したように、\(y = a\sin bx\) の \(a\) はグラフの振幅を、\(b\) はグラフの周期(周波数)を表します。
だからコサインのグラフもサインのグラフも、下にいくほど振幅はちょっとずつ小さくなってますよね。
また周期は短くなっていってますよね(周波数が大きくなってますよね)。
ここまでは数Ⅱの知識でわかると思います。
単純なグラフを足し合わせると複雑な形になる不思議
それなのに、こうした単純な三角関数どうしを足し合わせることで、複雑な形のグラフになっちゃうんです。
もういちどそのグラフを掲げると、これ↓

このグラフの式は以下のとおりです。
$$\begin{eqnarray}f(x) &=& \frac{2}{3}\cos x + \frac{2}{3}\sin x \\&+& \frac{4}{9}\cos 2x + \frac{3}{5}\sin 2x
\\&+& \frac{8}{27}\cos 3x + \frac{4}{7}\sin 3x \\&+& \frac{16}{81}\cos 4x + \frac{5}{9}\sin 4x
\\&+& \frac{32}{243}\cos 5x + \frac{6}{11}\sin 5x \\&+& \frac{64}{729}\cos 6x + \frac{7}{13}\sin 6x
\\&+& \frac{128}{2187}\cos 7x + \frac{8}{15}\sin 7x\end{eqnarray}\tag{1}$$
足し算しただけですよね。不思議ですねー。
以下のページでも、この不思議を味わえます。
フーリエ級数実演(EMANの物理学「フーリエ級数の基本」ページより)
指示にしたがって、自由に波の形を描いてみてください。んで「次へ」ボタンを何度も押していくと、だんだんその波の形に近づいていくはずです。
下には1個1個の三角関数が表示されます。
フリーハンドで自由に描いた波なのに、三角関数の足し合わせで表現されちゃう不思議。
いやー、おもしろい!
ちなみにEMANさんのサイトではいつも楽しく数学・物理を勉強させてもらってます。
いくつか書籍化もされてますね。
数字を決めるときのルール
ただ1個1個の三角関数の係数は、でたらめに決めてるわけじゃありません。
つまり\(y = a\sin bx\) の \(a\) と \(b\) は、ルールに従って決められています。
上でちょろっと述べたのはこのことです。
じつはその数字を決めるルールが、フーリエ級数のあの数式なんです。
ってことで、次はいよいよ数式の中身を理解していきます。
フーリエ級数を理解しよう

↑のフーリエ級数の数式を理解するのがこの記事のテーマです。
すこしずつ、にじりよっていきましょう。
コサインとサインの係数 \(a_n\) 、 \(b_n\)
上で使った14個の三角関数。
コサインが7個、サインが7個ありました。
それぞれの係数だけを書きだしてみると、以下のとおりです。
\(\cos \) の係数
$$\frac{2}{3}~~\frac{4}{9}~~\frac{8}{27}~~\frac{16}{81}~~\frac{32}{243}~~\frac{64}{729}~~\frac{128}{2187}$$
\(\sin \) の係数
$$\frac{2}{3}~~\frac{3}{5}~~\frac{4}{7}~~\frac{5}{9}~~\frac{6}{11}~~\frac{7}{13}~~\frac{8}{15}$$
このように数が並んだものを数列といいましたね。
よって \(\cos \) の係数の数列を \(\large{a_n}\) 、\(\sin \) の係数の数列を \(\large{b_n}\) と呼ぶことにします。
いちおう、一般項は
$$a_n = \left(\frac{2}{3}\right)^{n}$$
$$b_n = \frac{n + 1}{2n + 1}$$
ってイメージで、数字を決めました。
「数列わすれた!」って人は数Bを復習してくださいね。
これで、より一般的に、\(cos \)の係数を \(a_n\)、\(sin \) の係数を \(b_n\) と表せるようになりました。
具体的な数列の数字、つまり \(a_n\) と \(b_n\) の中身は、波の形によって変わってきます。
波の形はそれこそ限りなくありますが、数列もまた限りなくあるんで、波の形にあわせて数字を決めればいいんです。
たとえば{10, 5, 8, 8, 9, 3, 1, 0, 4, 9, 9 }などの、いまテキトーに作った数列でも、なんらかの波の形ができるでしょう。
ちなみにこの数列の名前は「ジュウゴは白菜をよく食う」数列です。インスタントラーメンに入れると美味しいんですよ、とくに冬場は。
\(x\) の係数は1ずつ増える
つぎに \(x\) の係数を見てみましょう。
コサインの場合もサインの場合も、 \(x\) の前の数字が1ずつ増えていますね。
ってことは、数列のときとおなじように \(n\) を使って、
$$\cos \mathbf{n}x ~~~~\sin \mathbf{n}x $$
と、一般的に表すことができます。
以上のことから、上の例で挙げた (1) の式は、
\(a_n \cos nx + b_n \sin nx\) において、\(n=1\) から \(n=7\) までの7つをすべて足せばいい
ということがわかります。
足し算を表す \(\sum \) (シグマ)の記号を使う
ある数列をぜんぶ足し算したいときには、\(\sum \) という記号を使います。
「シグマ」と読みます。これも数Bの数列単元で習いましたね。
よって、上の例で挙げた(1)の式は、
$$f(x) = \displaystyle \sum_{ n = 1 }^{ 7 } [ a_n \cos nx + b_n \sin nx ]\tag{1′}$$
と表せます。
\(\sum \) の上下についている数字は、「\(n\) が1のときから7のときまで全部足せ」という意味です。
さあ、これでほぼフーリエ級数の形になりました!
「フーリエ級数とはコサインとサインを何度も足し合わせたもの」
「コサインとサインの係数は波の形によってちがうけど、なんらかの数列である」
「\(x\) の前の数字は1,2,3、・・・と1ずつ増えていく」
以上のことが理解できたと思います!
やっつけていない敵がまだ3匹いる・・・

え?まだフーリエ級数の形になってないって?
そうなんです。
フーリエ級数の式と、(1′)の式をくらべると、まだやっつけてない部分が3つあることに気づきます。
≪フーリエ級数≫$$f(x) = \frac{a_0}{2} + \displaystyle \sum_{ n = 1 }^{ \infty } \left[ a_n \cos \left( \frac{2\pi}{L}nx \right) + b_n \sin \left( \frac{2\pi}{L}nx \right) \right]$$
≪(1′)の式≫$$f(x) = \displaystyle \sum_{ n = 1 }^{ 7 } [ a_n \cos nx + b_n \sin nx ]$$
○\(\frac{a_0}{2}\) がくっついてる!
○\(n\) が7までじゃなくて\(\infty \)(無限大)まで足す?
○\(nx\) の前に\(\frac{2\pi}{L}\) なんてのがあるぞ!?
この3匹をやっつけたら、フーリエ級数の理解が完成です。
次回、ラストの記事でやっつけていきましょう!
乞うご期待!
2019/12/6追記
お待たせしました、三角関数の記事、完結編です↓

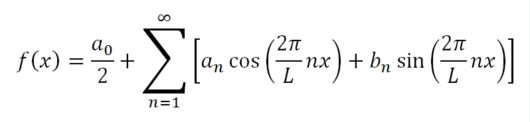





コメント
この続きはいつ発行されるのですか?
>ほほぴさん
説明がめんどうで後回しにしてて、いつのまにかすっかり忘れてました……
ごめんなさい……
2019年中には必ず公開しますm(_ _)m
了解です!ありがとうございます!楽しみにしてます
お待たせしました。
三角関数の記事「完結編」を12/6にUPしました。
よろしければご覧ください。
→三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③
返信遅くなってすみません!
本当にありがとうございます!
じゅうごさんの説明がわかりやすいので応援してます。
これからも頑張ってください!