三角比について2回目の記事になります。
今回は地図製作を例に、三角比がいまどのように役立っているのか、具体的にみていきます。
[この連載の記事一覧]
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)
三角比をつかった測量、つまり三角測量は、昔から地図をつくることに使われてきました。
日本では18世紀にヨーロッパから三角測量がもたらされ、江戸時代の伊能忠敬や、明治以降の陸軍、戦後は国土地理院が使用して、日本の正確な地図を作製してきました。
三角測量はとくに、海のむこうの島までの距離などを測るときに威力を発揮します。
たとえばこんなとき↓

さて、新潟から佐渡島までの距離は?柏崎から佐渡島までの距離は?
そして対岸から佐渡島までの距離は、いったいいくらでしょうか?
これ、海の上を歩いて測るわけにはいきませんよね。
この測量を三角比をつかってできるようになること。
そのためには、正弦定理と加法定理を使います。
そこでまずは、正弦定理と加法定理の紹介がてら、この2つの定理を証明してしまいます。
高校ではこの2つの定理は突然出てきて、証明なんかしないんですが、けっこうかんたんにできるので、ついでにやってしまいましょう。
正弦定理・加法定理の証明をおぼえておくと、忘れたときに導出しやすいですしね。
これから大学受験を控えている高校生の参考にもなると思います。
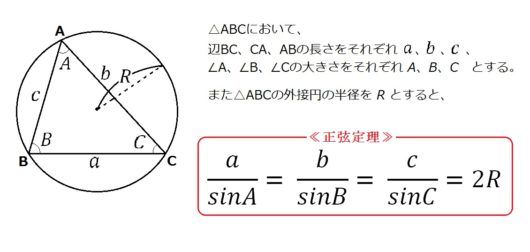
正弦定理を証明する
まずは↑の正弦定理を証明します。
ただ前回、「正弦定理がどのように出てきたのか、歴史の流れに沿って証明する」なんて大見得を切りましたが、調べてもよくわかりませんでしたm(_ _)m
なので証明についてはキッチリやりますが、歴史については憶測でしゃべりますんで、あしからず。
正弦定理は「円周角の定理」から
正弦定理の証明方法はいろいろありますが、今回、正弦定理の証明に使う道具は「円周角の定理」だけです。
円周角の定理とは「おなじ弧に対する円周角は等しい」とかのやつで、下の図のようなものです。中学3年生で習いましたね。
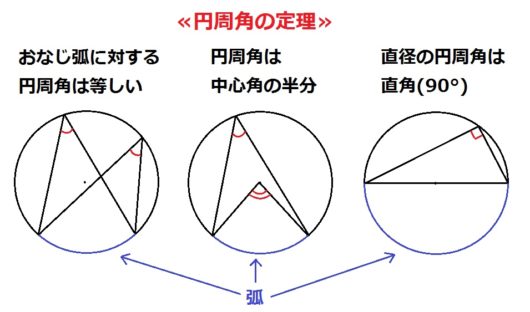
ちなみにまんなかの定理の特別版が、右の「直径の円周角は直角(90°)」です。
この右の定理は、紀元前6世紀のギリシアの学者タレスが証明しています。
またこの3つの定理すべて、紀元前3世紀ごろのギリシアの学者エウクレイデス(英語読みだとユークリッド)が『原論』という本のなかで証明しています。
だから、正弦定理が証明されたのもけっこう古いのかもしれません。
まあとにかく、じっさいに証明してみましょう。
\( \frac{a}{sinA} = 2R\) の証明
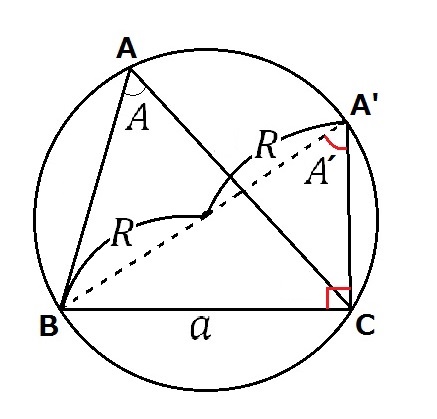
図のようにA’をとると、A’Bは直径だから、△A’BCは直角三角形になります(円周角の定理:右より)。
直角三角形A’BCで、サインの定義より、$$sinA’ = \frac{a}{2R}$$
式を変形して、$$\frac{a}{sinA’} = 2R$$
円周角の定理:左より、A‘ = Aだから、$$\frac{a}{sinA} = 2R\tag{1}$$
あとは\(sinB\) についても、\(sinC\) についても同様です。
\( \frac{b}{sinB} =2R\)、\( \frac{c}{sinC} =2R\) の証明
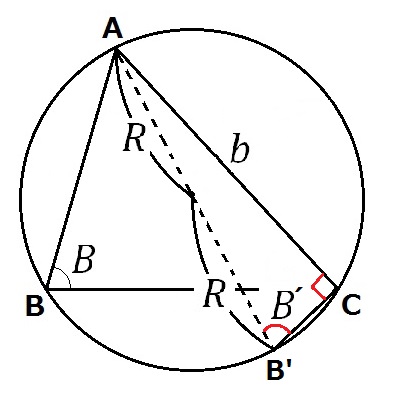
図のようにB’をとると、AB’は直径だから、△AB’Cは直角三角形になります(円周角の定理:右より)。
直角三角形AB’Cで、サインの定義より、$$sinB’ = \frac{b}{2R}$$
式を変形して、$$\frac{b}{sinB’} = 2R$$
円周角の定理:左より、B‘ = Bだから、$$\frac{b}{sinB} = 2R\tag{2}$$
\(sinC\) も同様の手順だから省略します。そんで$$\frac{c}{sinC} = 2R\tag{3}$$
以上、(1)(2)(3)より、$$\large{\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2R}$$
このようにして、円周角の定理を使ってかんたんに正弦定理が証明できるんです。
加法定理を証明する
正弦定理につづいて、数Ⅱで出てくる「加法定理」を証明します。
これを証明し終わったら、いよいよ三角測量に入っていきますので、もうちょっとだけ付き合ってください。
加法定理は「トレミーの定理」から
加法定理の証明方法も、正弦定理とおなじくいろいろありますが、数Aの「図形の性質」で習う「トレミーの定理」からも出すことができます。
そして歴史的な経緯でいえば、どうもこの「トレミーの定理」によって証明されたのが加法定理らしいんです。
だれが証明したのかはよくわかりませんでした。
もしかしてトレミーさん本人、つまり当時の言葉で呼ぶならプトレマイオスさんが証明したのかもしれません。
プトレマイオスは2世紀にアレクサンドリアで活躍した学者です。
天動説を集大成した人としても有名ですね。
ちなみに前回の記事で紹介したヒッパルコスも、『原論』を書いたエウクレイデスも、みんなエジプトのアレクサンドリアで活躍した人たちです。
いかに古代ギリシア・ローマ時代をつうじて、アレクサンドリアが学問のメッカだったかがわかります。
(なぜアレクサンドリアで学問が花開いたのか、かんたんにわかる記事はこちら)
このプトレマイオスが証明した「トレミーの定理」とは、↓のようなものです。
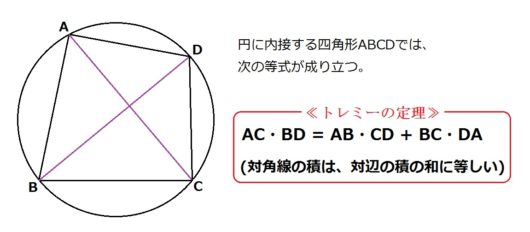
この定理をつかって、プトレマイオスは加法定理を導き出しました。
ではどのように導き出すのか、じっさいに証明してみましょう。
sin(α+β)=・・・の式を出す
まず↓の図のように、円に内接する四角形ABCDをちょっと特別にします。
つまり対角線BDが円の直径になるようにして、しかもその直径の長さを1とするんです。
また∠ABDをα(アルファ)、∠CBDをβ(ベータ)としておきます。

BDは直径なので、円周角の定理より、∠Aと∠Cは直角になります。
直角三角形ABDにおいて、サインとコサインの定義より、$$sinα = \frac{DA}{1} 、cosα = \frac{AB}{1}$$
つまり、$$DA = sinα 、AB = cosα \tag{1}$$
また直角三角形BCDにおいて、サインとコサインの定義より、$$sinβ = \frac{CD}{1} 、cosβ = \frac{BC}{1}$$
つまり、$$CD = sinβ 、BC = cosβ \tag{2}$$
今度は△ABCにおいて、正弦定理(\( \frac{AC}{sinB} = 直径(2R)\))を使って、$$\frac{AC}{sin(α+β)} = 1$$
つまり、$$AC = sin(α+β) \tag{3}$$
以上(1)(2)(3)とBD=1を、
トレミーの定理 AC・BD = AB・CD + BC・DA に代入すると、$$sin(α+β) × 1 = cosαsinβ + cosβsinα$$
つまり、$$\large{sin(α+β) = sinαcosβ + cosαsinβ}$$と、加法定理のうち1つだけ出てくるんです。
残り5つを出す
あとはこのsin(α+β)=・・・の式を順々に式変形して、残りの5つを出すだけです。
ひたすら数式の変形なので、数式イヤだ!って人は読み飛ばしてかまいません。
$$\begin{eqnarray}sin(α-β) &=& sin\left\{α+(-β)\right\} \\ &=& sinαcos(-β) + cosαsin(-β) \\ &=& \large{sinαcosβ – cosαsinβ}\end{eqnarray}$$
$$\begin{eqnarray}cos(α+β) &=& sin\left\{90°-(α+β)\right\} \\ &=& sin\left\{(90°-α)-β)\right\} \\ &=& sin(90°-α)cosβ – cos(90°-α)sinβ \\ &=& \large{cosαcosβ – sinαsinβ}\end{eqnarray}$$
$$\begin{eqnarray}cos(α-β) &=& cos\left\{α+(-β)\right\} \\ &=& cosαcos(-β) – sinαsin(-β) \\ &=& \large{cosαcosβ + sinαsinβ}\end{eqnarray}$$
$$\begin{eqnarray}tan(α+β) &=& \frac{sin(α+β)}{cos(α+β)} \\ &=& \frac{sinαcosβ + cosαsinβ}{cosαcosβ – sinαsinβ} \\ &=& \frac{\frac{sinαcosβ + cosαsinβ}{cosαcosβ}}{\frac{cosαcosβ – sinαsinβ}{cosαcosβ}} \\ &=& \frac{\frac{sinα}{cosα} + \frac{sinβ}{cosβ}}{1 – \frac{sinαsinβ}{cosαcosβ}} \\ &=& \large{\frac{tanα + tanβ}{1 – tanαtanβ}}\end{eqnarray}$$
$$\begin{eqnarray}tan(α-β) &=& tan\left\{α+(-β)\right\} \\ &=& \frac{tanα + tan(-β)}{1 – tanαtan(-β)} \\ &=& \large{\frac{tanα – tanβ}{1 + tanαtanβ}}\end{eqnarray}$$
はい、以上です。
おつかれさまでした。
さあ、三角測量をしよう!

正弦定理と加法定理を証明し終えたので、いよいよこの2つを使って、佐渡島までの距離を求めていきます。
まずは正弦定理を使い、新潟および柏崎から佐渡島までの距離を求めます。
そして加法定理を使い、対岸から佐渡島までの距離を求めていきます。
どちらもかんたんに出るのでパパッとやっちゃいましょう。
新潟、柏崎から佐渡島までの距離
まず図のように、新潟―柏崎の直線距離は75kmとします。
またそれぞれから佐渡島を向いた角度は、54°、37℃だったとします。
すると残りの角度は89°とわかりますね。三角形の内角の和180°から引けばいいから。
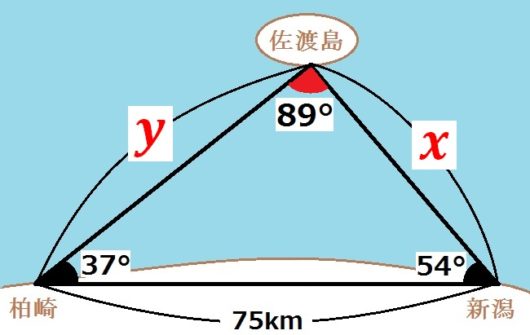
まずは\(x\)を求めます。正弦定理より、$$\frac{x}{sin37°} = \frac{75}{sin89°}$$
式を変形して、$$x = \frac{75}{sin89°} \times sin37°$$
ここで前回も使った「三角比の表」を見ると、\(sin89° = 0.9998\)、\(sin37° = 0.6018\) です。これらを代入して、$$x = \frac{75}{0.9998} \times 0.6018 = 45.144・・・$$
新潟から佐渡島までの距離は約45kmとわかります。
つぎに\(y\)も求めます。正弦定理より、$$\frac{y}{sin54°} = \frac{75}{sin89°}$$
式を変形して、$$y = \frac{75}{sin89°} \times sin54°$$
「三角比の表」から、\(sin54° = 0.8090\) なので、代入して、$$y = \frac{75}{0.9998} \times 0.8090 = 60.687・・・$$
柏崎から佐渡島までの距離は約61kmとわかります。
対岸から佐渡島までの距離
下図の\(z\) をもとめます。
ただ海岸線が微妙にふくらんでいるので、正確にいえば「ほぼ対岸から佐渡島まで」の距離になります。
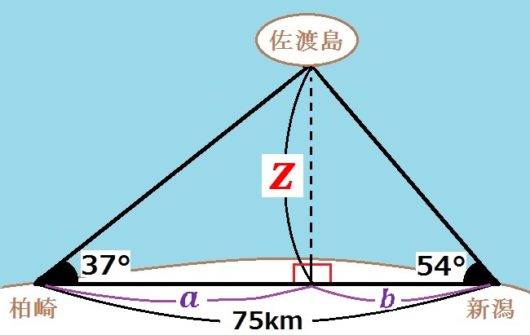
海岸線の左側の長さを\(a\)、右側の長さを\(b\) とします。
左側の直角三角形より、タンジェントの定義から、$$tan37° = \frac{z}{a}$$
同様に、右側の直角三角形より、タンジェントの定義から、$$tan54° = \frac{z}{b}$$
これらの式を変形すると、$$a = \frac{z}{tan37°}、b = \frac{z}{tan54°}$$
よって、$$a + b = \large{\frac{z}{tan37°} + \frac{z}{tan54°} = 75}$$
後半の等式を\(z\) について変形すると、$$z = \frac{75}{\frac{1}{tan37°} + \frac{1}{tan54°}}$$
「三角比の表」より\(tan37° = 0.7536\)、\(tan54° = 1.3764\) なので、代入して計算すると、$$z = 36.52・・・$$
対岸から佐渡島までは約37kmとわかります。
三角比による三角形の高さの一般的な求め方
「おい、加法定理ぜんぜん使わなかったじゃねえか」と思ったあなた。
するどいです。使わなかったんです。
あれ?なんでだ???(汗)
そう、37°とか54°とか75kmとかじゃなくて、一般的な求め方で加法定理を使うんだった!
つまりこういうことです↓
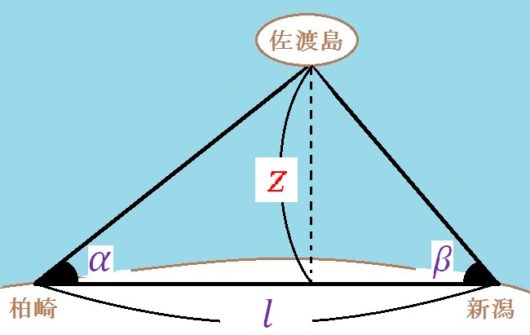
37°の代わりに\(α\)、54°の代わりに\(β\)、75kmの代わりに\(l\) とおきます。
すると上の最後の式は$$z = \frac{l}{\frac{1}{tanα} + \frac{1}{tanβ}}$$
となります。
これを変形していきます。
$$\begin{eqnarray} &=& \frac{l}{\frac{cosα}{sinα} + \frac{cosβ}{sinβ}} = \frac{l}{\frac{sinαcosβ + oosαsinβ}{sinαsinβ}} \\ &=& \frac{l}{\frac{sin(α+β)}{sinαsinβ}} \\ &=& \frac{sinαsinβ}{sin(α+β)}l\end{eqnarray}$$
2つめから3つめの式になるときに、加法定理(の逆)を使いましたね!
ふー、よかった!
そんで、最後に出てきた式に角度と長さを代入すれば\(z\) が求まります。代入してみると、$$\frac{sin37°sin54°}{sin(37°+54°)} \times 75 = 36.52・・・$$
約37kmと、おなじ答えが出ました。
一般的に、底辺 \(l\) とその両端の角度 \(α、β\) がわかっている三角形で、高さ \(d\) を出したいときには、$$\large{d = \frac{sinαsinβ}{sin(α+β)}l}$$という公式が使えます。
おぼえておくと便利かもしれません。
おわりに
ここまで正弦定理と加法定理を証明し、そしてこの2つの定理を使って、三角測量とはじっさいどういう計算をするのか見てきました。
三角比が役に立つ学問なんだと理解してもらえれば、ジュウゴとしてはじゅうぶんです。
ちなみに、国土地理院では今、光を使った測距儀や、GPSなどを使って、より正確な地図を作製しています。
だから上で説明した三角測量の方法はあくまで原理にすぎません。あしからず。
ほかにも三角比は設計や建築などの分野で、いまも使われています。
三角比がないと、ビルも建たないし、クレーン車も倒れてしまいます。
日常的に仕事で使っている人からしたら「なにをいまさら。毎日サイン、コサイン、タンジェントばっかりだよ」と言われそうです。
でもジュウゴのように日頃数学を使わない人間にとっては、今回記事を書くにあたりいろいろ勉強して、「へえー、こういうふうに使われているんだ」と驚くことばかりでした。
理系と文系の乖離って、こわいですね。
そしてじつは、三角比から発展した「三角関数」という分野が、もっともっと多くの職業で使われているんです。
「三角関数」がないと、ぼくらは音楽を聴けないし、電気を使えないし、健康診断も受けられません。
次回からはこの「三角関数」について書いてみようと思います。
→ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
[この連載の記事一覧]
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)



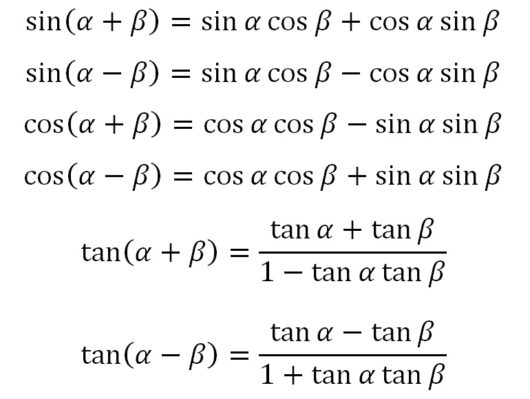





コメント
対岸から佐渡島までの距離について
佐渡島、柏崎、対岸の三角形で三角比を使えばすぐに出ますよ。
佐渡島(A)、柏崎(B)、対岸(C)として
sin37°はAC/ABで求まり、ABの数値は既に出ているのでSin37×60.687をするだけです。
ありがとうございます。助かりました。