中学生の数学の勉強における「なぜ?」を、根本からわかりやすく解説します。
今回は、中2数学「式の計算」単元に出てくる「式による説明」。
そのコツと説明の仕方。
そしてなぜこんなメンドイことをするのかの理由まで解き明かします。
いきなりですが、「式による説明」問題はたとえばこんなの↓
例題1)偶数と奇数の和は奇数になる。このわけを説明せよ。
解答例)\(m\) , \(n\) を整数とすると、
偶数は \(2m\) 、奇数は \(2n+1\) と表せる。
\begin{eqnarray} & & 2m+(2n+1) \\ &=& 2m+2n+1 \\ &=& 2(m+n)+1 \end{eqnarray}
\(m+n\) は整数なので、\(2(m+n)+1\) は奇数である。
よって、偶数と奇数の和は奇数になる。

ここで中学生がつまずく原因は、主に3つです。
- 「偶数」「奇数」「2けたの自然数」「連続する整数」などの数を文字で表す、その準備が十分にできていない。
- 式による説明の仕方・流れがよくわかっていない。
- そもそもなぜ文字を使ってこんなことをするのか、疑問。
多くの参考書や数学教育のサイト、動画や学校の授業などはすべて、2.の解決に重点が置かれています。
よって数学の苦手な中学生は、1.の段階でつまずいてしまう。なんとなくわかるんだけど、自分でやろうとするとできない。こうなります。
また数学の得意な中学生でも、3.の疑問が解消されないままなので、正解することはできるけどモヤモヤが残ったまま。こうなってしまいます。
そこでこの記事では、1.2.3.すべてのつまずきを解消します。
中学数学で困っている生徒だけでなく、保護者さんや講師・家庭教師の方も参考にしてください。
1.「式による説明」に入る前の準備

まず「式による説明」では、出てくる数を文字を使って表す必要があります。
(なぜ文字で表す必要があるかは項目3で解説します)
ここでは、問題に出る数をすべて紹介するとともに、なぜそう表せるのかまで説明します。
15年の数学教育経験から、定期テストでよく出る数、模試や入試の難問でよく出る数、ぜんぶ網羅しました。
生徒はなぜそう表せるかの理由まで理解して、おぼえて使ってください。
偶数、奇数、倍数など
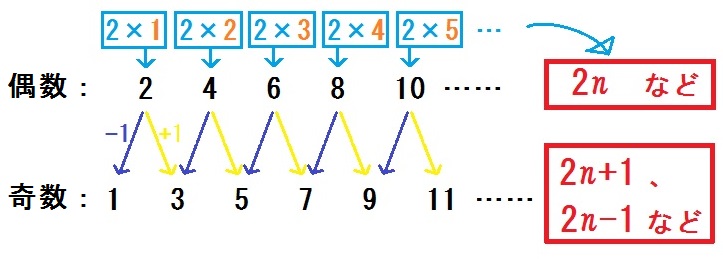
偶数とは、「 \(2 \times \mbox{(整数)}\) 」。
だって \(6=2\times3\) だし、\(98=2\times49\) 。
よって、\(m\) ,\(n\) という文字を整数とすると、
(使う文字は何でもいい。今後出てくる文字はすべて整数とします。)
奇数は、偶数より1多い・または1少ない数。
だって \(7=6+1\) だし、\(7=8-1\) 。
つまり奇数とは「 \(2\times \mbox{(整数)}+1\) 」または「 \(2\times \mbox{(整数)}-1\) 」。
3の倍数は、「 \(3\times \mbox{(整数)}\) 」。
「偶数=2の倍数」だから、同じ理屈。
ちなみに、同じ理屈で、
7の倍数:\(7p\) , \(7(x+y+1)\) …
99の倍数:\(99k\) , \(99(a-c)\) …
4で割りきれる数とは、4の倍数と同じこと。
ちなみに、同じ理屈で、
6で割りきれる数:\(6m\) , \(6(n+1)\) …
22で割りきれる数:\(22j\) , \(22(4k-5l+6m)\) …
5で割って2余る数は、「 \(5\times \mbox{(整数)}+2\) 」。
だって \(12= 5\times2 +2\) だし、\(37= 5\times7 +2\) 。
ちなみに、同じ理屈で、
8で割って3余る数:\(8a+3\) , \(8(b+c+9)+3\) …
11で割って10余る数:\(11p+10\) , \(11(q+r+s+t)+10\) …

2ケタの自然数など
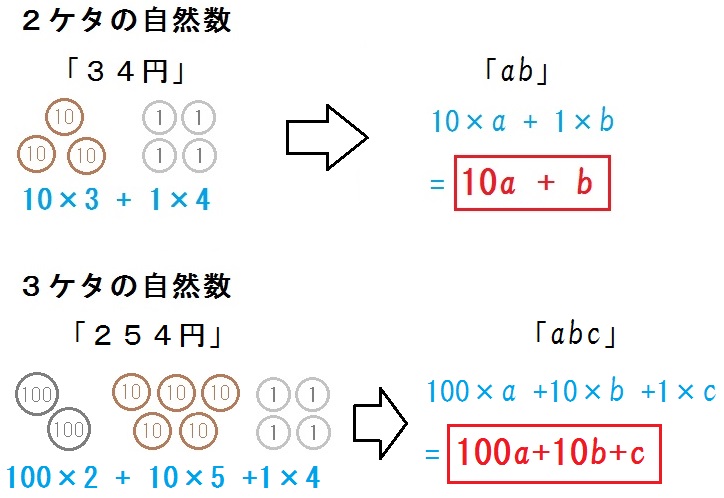
2ケタの自然数は \(10 \times \mbox{●} +\mbox{▲}\) 。
これはおカネで考えるとわかりやすい。
たとえば34円は「十円玉3枚+一円玉4枚」。
よって文字を使って表すと、
3ケタの自然数も同様。
たとえば254円は「百円玉2枚+十円玉5枚+一円玉4枚」。
よって、
ちなみに、同じ理屈で、
4ケタの自然数:\(1000a+100b+10c+d\) …
5ケタの自然数:\(10000a+1000b+100c+10d+e\) …
2つ以上の数
[32,76]のように、2つの偶数は関係ない。
だからちがう文字を使うこと。
[17,23]のように、2つの奇数も関係ない。
だからちがう文字を使うこと。
[3,4,5][46,47,48]のように、連続する3つの整数は1ずつ増える。
よって、このような表し方になる。
この場合は同じ文字を使うこと。
[4,6,8][10,12,14]のように、連続する3つの偶数は2ずつ増える。
よって、このような表し方になる。
やはり、連続する場合は同じ文字を使うこと。
[5,7,9][19,21,23]のように、連続する3つの奇数も2ずつ増える。
よって、このような表し方になる。
やはり、連続する場合は同じ文字を使うこと。
ちなみに、同様の理屈で、
連続する4つの偶数:[ \(2n-2\) , \(2n\) , \(2n+2\) , \(2n+4\) ]…
連続する5つの奇数:[ \(2n-3\) , \(2n-1\) , \(2n+1\) , \(2n+3\) , \(2n+5\) ]…
などとなる。

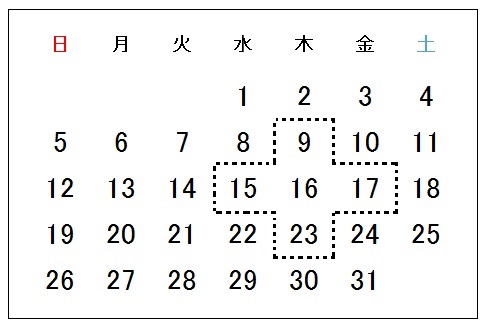
カレンダー
下の図のように囲む。
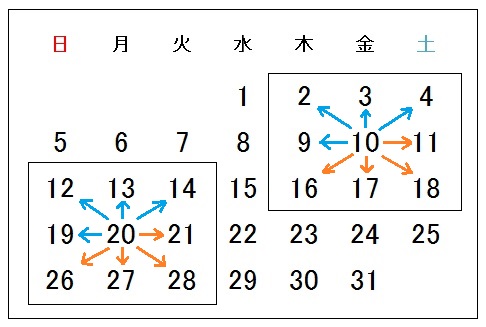
すると、どこを囲んでも、まんなかを基準にして、
- 左上:(まんなか)-8
- 上:(まんなか)-7
- 右上:(まんなか)-6
- 左:(まんなか)-1
- 右:(まんなか)+1
- 左下:(まんなか)+6
- 下:(まんなか)+7
- 右下:(まんなか)+8
よって、まんなかの数を \(n\) とすると、
Amazonプライム・ビデオ「カレンダー・ガールズ(吹替版)」
以上、いろんな数を文字で表しました。
これで準備は完了。
いよいよ「式による説明」のコツ・手順に入りましょう。
ちなみに、「式による説明」などの整数問題で \(m\) , \(n\) などをよく使う理由。それは \(n\) が「number(数)」の頭文字だから。そして \(m\) は \(n\) のアルファベットいっこ手前の文字だからです。
逆に \(l\) や \(o\) や \(q\) や \(z\) 、\(g\) と \(j\) や \(u\) と \(v\) はあまり使いません。数字と間違ったり、両者を読み違えたりするからです。
それから、数学のほかの単元でよく使う文字も避ける傾向があります。
- 関数単元でよく使われる \(f\) , \(g\)
- 「高さ」「点」「半径」を表す \(h\) , \(p\) , \(r\)
- 「距離」「秒」「時間」を表す \(d\) , \(s\) , \(t\)
- 方程式で使われる \(x\) , \(y\)
- そして特定の数を指す \(e\) , \(i\) など
結果として、整数の証明でよく使う文字は \(a\) , \(b\) , \(c\) , \(k\) , \(m\) , \(n\) になるんです。
2.「式による説明」のコツ・手順

中学数学「式による説明」問題のコツは、以下4つの手順をふむことです。
- 登場人物を文字で表す
- 文章どおりに計算
- 結論の形にムリヤリもっていく
- 〆のことば
例をつかって説明します。
式による説明の流れ(前半)
例題1)偶数と奇数の和は奇数になる。このわけを説明せよ。
1.まずこの例題の登場人物は「偶数」と「奇数」の2人です。
この2人を、文字を使って表します。
この2人、「連続する○○」じゃないので、カップルでもなんでもない。
よってちがう文字を使って、
\(m\) , \(n\) を整数とすると、
偶数は \(2m\) 、奇数は \(2n+1\) と表せる。
とまず書く。
(使う文字が「整数だ」って最初に宣言することも必要です)

2.つぎに、文章どおりの計算式をつくります。
「式による説明」問題には、必ず計算を表す言葉が入ってます。
この例題でいうと、「和」。
つまりたし算です。よって、
(奇数の \(2n+1\) は多項式なので、かっこを付けておきましょう)
んで、かっこを外すとこうですね。

式による説明の流れ(後半)
3.そしてこの式を、結論の形にムリヤリもっていきます。
結論とは、「~になる」「~である」という文の~部分。
この例題でいうと「奇数」が結論です。
奇数の形って、「 \(2\times \mbox{(整数)}+1\) 」とかでしたね。
よって、ムリヤリがんばって、
( \(2m+2n=2(m+n)\) という式変形は、分配法則の逆を使っています。忘れたって人は以下の記事をみて復習してください↓)

4.最後に、〆(しめ)のことばを述べます。
「式による説明」の〆のことばは、決まっています。
一行目は「(かっこの中)は整数なので、(式全体)は(結論)である」。
二行目は「よって、(問題文を丸写し)」。
例題の場合、こうなります。
\(m+n\) は整数なので、\(2(m+n)+1\) は奇数である。
よって、偶数と奇数の和は奇数になる。

以上のように、
- 登場人物を文字で表す
- 文章どおりに計算
- 結論の形にムリヤリもっていく
- 〆のことば
この4手順で書いていく。
これが中学数学「式による説明」のコツになります。
一緒にやってみよう(問題)
とはいえ、いきなり中学生に「わかったね、さあ、やってごらん」というのも酷な話。
特に「3.結論の形にムリヤリもっていく」は、慣れが必要です。
そこで、数問は一緒に解いていくといいでしょう。
以下にそれ用の例題をいくつか用意しました。
どれも「式による説明」のなかでは難問の部類に入りますが、だからこそ一緒がいい。
どうぞご活用ください。
例題2)7で割ると2余る数と、7で割ると5余る数の和は7の倍数になる。このわけを説明せよ。
例題3)連続する3つの奇数の和にさらに3を加えると、6の倍数になることを説明せよ。
例題4)一の位が0でない3ケタの自然数と、その自然数の百の位と一の位を入れかえた自然数との差は、11の倍数である。このことを説明せよ。
例題5)たとえば3ケタの整数792の、各位の数の和は \(7+9+2=18\) で9の倍数である。このとき、792という数それ自体も9の倍数になっている。このように、各位の数の和が9の倍数になる3ケタの整数は9の倍数である。このわけを説明せよ。
例題6)右図のように、カレンダーを十字の形に囲むと、囲まれた5つの数の和はまんなかの数の5倍になることを説明せよ。
どれもそこそこの難問。
特に例題5は「式による説明」における超難問です。
ただ定番問題でもあるので、ぜひチャレンジしてみてください。
一緒にやってみよう(解答)
では解答例をどうぞ。
例題2)7で割ると2余る数と、7で割ると5余る数の和は7の倍数になる。このわけを説明せよ。
解答例)\(m\) , \(n\) を整数とすると、
7で割ると2余る数は \(7m+2\) 、
7で割ると5余る数は \(7n+5\) と表せる。
\begin{eqnarray} & & (7m+2)+(7n+5) \\ &=& 7m+2+7n+5 \\ &=& 7m+7n+7 \\ &=& 7(m+n+1) \end{eqnarray}
\(m+n+1\) は整数なので、\(7(m+n+1)\) は7の倍数である。
よって、7で割ると2余る数と、7で割ると5余る数の和は7の倍数になる。
例題3)連続する3つの奇数の和にさらに3を加えると、6の倍数になることを説明せよ。
解答例)\(n\) を整数とすると、
連続する3つの奇数は \(2n-1\) , \(2n+1\) , \(2n+3\) と表せる。
\begin{eqnarray} & & (2n-1)+(2n+1)+(2n+3)+3 \\ &=& 2n-1+2n+1+2n+3+3 \\ &=& 6n+6 \\ &=& 6(n+1) \end{eqnarray}
\(n+1\) は整数なので、\(6(n+1)\) は6の倍数である。
よって、連続する3つの奇数の和にさらに3を加えると、6の倍数になる。
例題4)一の位が0でない3ケタの自然数と、その自然数の百の位と一の位を入れかえた自然数との差は、11の倍数である。このことを説明せよ。
解答例)3ケタの自然数の百の位、十の位、一の位の数をそれぞれ \(a\) , \(b\) , \(c\) とすると、
3ケタの自然数は \(100a+10b+c\) 、
入れかえた自然数は \(100c+10b+a\) と表せる。
\begin{eqnarray} & & (100a+10b+c)-(100c+10b+a) \\ &=& 100a+10b+c-100c-10b-a \\ &=& 99a-99c \\ &=& 11(9a-9c) \end{eqnarray}
\(9a-9c\) は整数なので、\(11(9a-9c)\) は11の倍数である。
よって、一の位が0でない3ケタの自然数と、その自然数の百の位と一の位を入れかえた自然数との差は、11の倍数である。
例題5)たとえば3ケタの整数792の、各位の数の和は \(7+9+2=18\) で9の倍数である。このとき、792という数それ自体も9の倍数になっている。このように、各位の数の和が9の倍数になる3ケタの整数は9の倍数である。このわけを説明せよ。
解答例)3ケタの整数の百の位、十の位、一の位の数をそれぞれ \(a\) , \(b\) , \(c\) とすると、
3ケタの整数は \(100a+10b+c\) と表せる。
\begin{eqnarray} & & 100a+10b+c \\ &=& 99a+a+9b+b+c \\ &=& 99a+9b+(a+b+c)\tag{1} \end{eqnarray}
ここで、各位の数の和が9の倍数なので、\(k\) を整数とすると、
\(a+b+c=9k\) と表せる。
よって(1)式は、
\begin{eqnarray} & & 99a+9b+9k \\ &=& 9(11a+b+k) \end{eqnarray}
\(11a+b+k\) は整数なので、\(9(11a+b+k)\) は9の倍数である。
よって、各位の数の和が9の倍数になる3ケタの整数は9の倍数である。
例題6)右図のように、カレンダーを十字の形に囲むと、囲まれた5つの数の和はまんなかの数の5倍になることを説明せよ。
解答例)まんなかの数を \(n\) とすると、
5つの数は \(n-7\) , \(n-1\) , \(n\) , \(n+1\) , \(n+7\) と表せる。
\begin{eqnarray} & & (n-7)+(n-1)+n+(n+1)+(n+7) \\ &=& n-7+n-1+n+n+1+n+7 \\ &=& 5n \end{eqnarray}
よって、囲まれた5つの数の和はまんなかの数の5倍になる。
質問・疑問などはコメント欄からお寄せください。
3.なぜ文字を使って説明するのか?

この記事の最後として、「なぜ文字を使ってわざわざこんなコトをするのか?」という疑問に回答します。
答えは以下3点です。
- 数学という学問を生み出した古代ギリシア人が「絶対確実な永遠不変の真理」を求める性格だったため、
- 数学は例外をひとつも許さない、厳密な学問になった。よって、数学上でなにか真理を求めるときには「あらゆる場合に当てはまる」と厳密に証明しないといけないが、
- 文字を使えば、これが可能になる。つまり無限にある数をすべて試したことになるから。
とくに3.の「文字を使えば無限をカバーできる」ってトコロが重要です。
たとえば例題1の
という証明を、
\(2+1=3\) , \(4+5=9\) , \(8+13=21\) ……
試したかぎり、必ずそうなるから。
とやっては、試してないパターンがたくさんあって証明になりません。
しかし、かといって、無限にある数をすべて試すわけにもいかない。
そこで文字を使うんです。
「この文字にはどんな数を当てはめてもいい。だから文字を使って証明したら、それは無限にある数をすべて試したことになる」からです。
*このあたりの詳しい話は数学コラムで別に解説しています↓
まとめ
○いろんな数を文字で表すと以下のとおり。
偶数:\(2m\)
奇数:\(2n+1\)
3の倍数:\(3mn\)
4で割りきれる数:\(4(m+1)\)
5で割って2余る数:\(5n+2\)
2ケタの自然数:\(10a+b\)
3ケタの自然数:\(100a+10b+c\)
連続する整数:[\(n-1\) , \(n\) , \(n+1\)]
連続する偶数:[\(2n-2\) , \(2n\) , \(2n+2\)]
連続する奇数:[\(2n-1\) , \(2n+1\) , \(2n+3\)]
カレンダー:→
○「式による説明」のコツは、以下4つの手順をふむこと。
- 登場人物を文字で表す
- 文章どおりに計算
- 結論の形にムリヤリもっていく
- 〆のことば

○なぜ「式による説明」で文字を使うのか?
文字を使えば、無限をカバーできるから。
つまり、文字にはどんな数を当てはめてもいいので、無限にある数をすべて試したことになるから。
以上、「式による説明」のコツでした。
中学生自身の勉強や、中学数学を教える方の参考にしてください。
[関連記事]
数学の証明ってなに?なんで証明するの?なぜ文字を使うの?
次回は同じく中2 式の計算より
「等式の変形」を解説します↓









コメント
すごい
23で割り切れる数のところ、22で割り切れる数だと思います。
ご指摘ありがとうございます。
修正しました。
1.の段階、とても大切ですね。
1年次に習ったことではあるけれど、たいていの生徒は抜けているので、
再確認することが必要ですね。
もっと詳しく説明お願いします