中学数学「平方根」のコツ② 有理数と無理数／循環小数と分数

中学数学のつまずき解消をめざすこの連載。

中３「平方根」の２回目は

• 有理数・無理数とは何か
• 循環小数⇔分数の変換のしかた

を解説します。

ここで中学生がつまずくポイントは主に２点。

• 授業がさらっと進んじゃって、数の分類や全体像がよくわからない
• 循環小数を分数で表す問題がむずかしい

そこで、ジュウゴがいつも使う教え方のコツを紹介します。

前者のコツは、数学の歴史とあわせて数を分類すること。

後者のコツは、ひとつひとつの手順を定着させることだけです。

[前回の記事]
中学数学「平方根」のコツ① 平方根とは／平方根の大小

無理数が出てくる歴史

まず有理数・無理数とは何かを解説するには、人類が数を拡張させてきた歴史をかんたんに紹介するといいでしょう。

以下に紹介する数学史の知識を、ぜひ指導にお役立てください。

自然数、分数

ではここで、いままでに習ったいろんな数を分類してみよう。

まず \(1,2,100\) といった、ものを数える時に使う数。

これはぼくらにとっていちばん自然な数だから、「自然数」という。

人類の歴史が始まって以来、この自然数はずっと使われてきました。

 

次に人類が生み出したのが「分数」。

つまり \(\frac{1}{3}\) とか \(\frac{7}{10}\) とかで、「肉を３等分したうちの１つ」とか、「土地を10等分したうちの７個分」というように、分数も古くから使われてきた数です。

ちなみに、この分数をちゃんと数のひとつとして扱ったのが、古代ギリシアのピタゴラス学派という人たち。

中３の終わりに「三平方の定理」というのを習うけど、その定理を生み出したピタゴラスのお弟子さんたちです。

紀元前6-5世紀ころのことみたい。

 

0、負の数、小数

それ以降、約1000年間、人類は自然数と分数という２種類だけが数だと思ってた。

でも紀元5世紀ころ、インドで「0」という数が誕生します。

「ない」ということを表すゼロが、数のひとつになった。これは数学史上の大事件なんだけど、語ると長くなるからやめます。

知りたいひとは下の本を読んでみてね。

 

つづいて6-7世紀ころ、同じくインドで「負の数」も使われはじめます。

つまりマイナスのことで、\(-3\) とか \(-1000\) とか。

負の数は、会計上の必要から生み出されました。貯金がプラス、じゃ借金はマイナスってぐあいです。

こうして自然数と分数は、０を含めたマイナスの領域にまで拡張されました。

そして分数じゃない数を特別に「整数」と呼ぶようになりました。

時代がくだって15-16世紀ころになると、「小数」という表記方法が登場します。

小数とは分数の代わりになる表し方で、つまり分数の分子÷分母をしたもの。

$$ \frac{2}{5} = 2 \div 5 = 0.4 $$

ってことね。

逆に

$$ 0.4 = \frac{4}{10} = \frac{2}{5} $$

と小数を分数になおすこともできる。

つまり分数と小数って表記方法がちがうだけで、同じ数を表しています。

 

無理数の登場

ついでに言うと、整数もぜんぶ分数で表すことができる。

$$ 1 = \frac{1}{1} \ , \ 0 = \frac{0}{1} \ , \ -3=- \frac{3}{1} $$

じゃ、「数はぜんぶ分数で表せる」と言いたくなるよね？

しかし、分数で表せない数があることを、人類はすでに知っていた。

これが１回目の記事でみたとおり、２の平方根。

\( \sqrt{2}\) が分数で表せないことは、紀元前３世紀ころにエウクレイデス（ユークリッド）というギリシア人が証明してました。

 

ただ人類はそれから1000年以上、２の平方根を数の仲間に入れることを拒んでいた。

はじめてこれを「数のひとつだ」としたのは、中世のイスラーム学者たち。

９世紀のアル・ファーラービー、11世紀のウマル・ハイヤームといった哲学者たちが、分数で表せない数も数の仲間に入れて、これを「無理数」と呼んだ。

こうしたイスラームの知識がヨーロッパに輸入されて、15世紀ころに「根」という意味のラテン語radixの頭文字「r」をとって、ルートという記号が作られた。

[関連記事]
ヨーロッパの歴史の流れを超簡単にまとめてみた

 

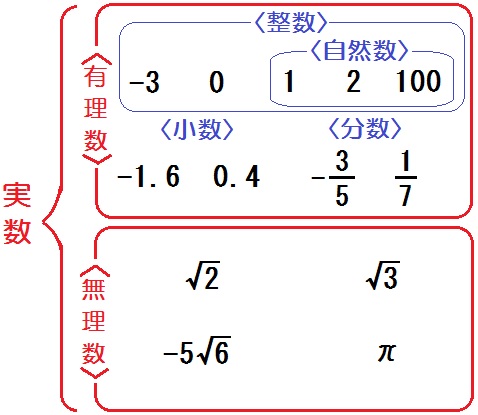
有理数・無理数とは

つまり有理数とは、分数で表すことのできる数。

無理数とは、分数で表すことのできない数。

そして有理数と無理数をあわせて「実数」と呼び、これが数の全体です。

つまり数直線上に切れ目なく並んでいる数すべてです。

（高校数学で「虚数」というのも習うけど、今回は省略）

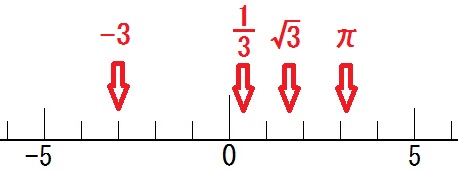
たとえば \(0.33333 \cdots \) は有理数。\( = \frac{1}{3}\) と表せるから。

また \(\sqrt{25}\) も有理数。\(=5=\frac{5}{1}\) だから。

でも \(\sqrt{3}\) は無理数。分数で表せない。

そして \( \pi\) も無理数。円周率もじつは分数で表せないんだ。

以上が有理数と無理数のちがい。

そして人類が数を拡張してきた歴史でした。

＞Amazonプライム・ビデオで「奇蹟がくれた数式(字幕版)」を観る

 

分数を循環小数で表す

つづいて、分数を循環小数で表すやり方を紹介します。

ここは次の「循環小数を分数で表す問題」のイントロダクションなので、さらっといきましょう。

循環小数とは

ところで、分数を小数で表したとき、わり切れずに数字がずっとつづくやつがある。

たとえば \(\frac{3}{5}\) は

$$ \frac{3}{5} = 3 \div 5 = 0.6 $$

とわり切れるけど、\(\frac{1}{7}\) は

$$ \frac{1}{7} = 1 \div 7 = 0.142857142857 \cdots $$

と、無限に「142857」がくりかえす。

このように、きまった数字がくりかえす小数を「循環小数」といいます。

じゃ、無限につづく小数はすべて循環小数かというと、そうじゃない。

無理数の場合は循環小数になりません。

\(\sqrt{3}\) も \(\pi\) も、どこまでいっても次にくる数字は決まっていない。

だから循環小数になるのは有理数の一部、つまり分数の一部だけってこと。

[関連記事]
中学数学「平面図形」のコツ⑤ 円とおうぎ形

 

やり方

循環小数の表し方にはルールがあります。

論より証拠、みてて。

\begin{eqnarray} \frac{5}{9} &=& 5 \div 9 \\ &=& 0.555 \cdots \\ &=& 0.\dot{5} \end{eqnarray}

\begin{eqnarray} \frac{5}{12} &=& 5 \div 12 \\ &=& 0.41666 \cdots \\ &=& 0.41\dot{6} \end{eqnarray}

\begin{eqnarray} \frac{4}{11} &=& 4 \div 11 \\ &=& 0.363636 \cdots \\ &=& 0.\dot{3}\dot{6} \end{eqnarray}

\begin{eqnarray} \frac{1}{7} &=& 4 \div 11 \\ &=& 0.142857142857 \cdots \\ &=& 0.\dot{1}4285\dot{7} \end{eqnarray}

\begin{eqnarray} \frac{3}{14} &=& 3 \div 14 \\ &=& 0.2142857142857 \cdots \\ &=& 0.2\dot{1}4285\dot{7} \end{eqnarray}

くりかえす数字の上に点を打てばいいんだ。

くりかえす部分が２ケタ以上なら、くりかえしの最初と最後に点を打てばいい。

これが分数を循環小数で表すやり方です。

＞Amazonプライム・ビデオで「最高の人生の見つけ方 (字幕版)」を観る

 

循環小数を分数で表す

そしていよいよ、循環小数を分数で表すやり方。

ここは手順を分けて示し、そしていつもの方法で定着をはかるといいでしょう。

やり方（前半）

では、今度は逆に、循環小数を分数で表してみよう。

例題のような問題を解くには、以下４つの手順をふむといい。

≪循環小数を分数で表す手順≫

1. \(x= \mbox{循環小数}\) とおく…①
2. ①の両辺を10倍、100倍などする…②
3. ②－①で小数点以下を消す
4. \(x\) を求める

例題の1.を、じっさいにやってみせます。

 

やり方（後半）

やり方はわかったね。

じゃ、例題の2.を一緒にやってみよう。

まず \(x=0.\dot{2}\dot{3}\) とおく。

点を使わずに循環小数を表したら

$$ x=0.2323 \cdots \ \large{\mbox{…①}} $$

だ。

次に①の両辺を10倍 or 100倍 or 1000倍…するんだけど、ポイントは「あとで引き算したら小数点以下がうまく消えるように」したいんだ。

①の両辺、何倍したらいい？

そう、100倍だね！

$$ 100x = 23.2323 \cdots \ \large{\mbox{…②}} $$

そんで②－①をしたら

\begin{eqnarray} 100x &=& 23.2323 \cdots \\ -) \qquad x &=& \ \ 0.2323 \cdots \\ \hline 99x &=& 23 \\ x &=& \frac{23}{99} \end{eqnarray}

答．\(\frac{23}{99}\)

このように、循環小数を分数で表すには

1. \(x= \mbox{循環小数}\) とおく…①
2. ①の両辺を10倍、100倍などする…②
3. ②－①で小数点以下を消す
4. \(x\) を求める

という手順でやること。

わかったら例題の3.を自力でやってみて。

（答えは \(\frac{437}{333}\) ）

 

練習問題

以上が循環小数→分数の指導例です。

このブログで毎度のように言ってますが、何か新しいことを教えるときには

まず要点をズバッと伝える
↓
じっさいにやってみせる
↓
一緒に解く
↓
させてみて、ほめる

という指導順が有効です。

「丁寧に教えてるんだけど生徒にちゃんと内容が入っていかない」という先生はぜひ参考にしてください。

 

では、やはり毎度のことですが、「わかる」を「できる」にするための練習問題を用意しました。

質問はコメント欄からどうぞ。

[関連記事]
中学数学「平方根」のコツ① 平方根とは／平方根の大小

 

まとめ

有理数とは、分数で表すことのできる数。
（\(0.4\) とか \(\frac{1}{7}\) とか）

無理数とは、分数で表すことのできない数。
（\(\sqrt{3}\) とか \(\pi\) とか）

分数→循環小数の手順は、
分子÷分母をしてくりかえす数字に点を打つだけ。

循環小数→分数の手順は、

1. \(x= \mbox{循環小数}\) とおく…①
2. ①の両辺を10倍、100倍などする…②
3. ②－①で小数点以下を消す
4. \(x\) を求める

という４段階でやること。

 

次回は「ルートを簡単にする計算」のコツを解説します。

このコツを習得すれば、

$$ \frac{3}{\sqrt{18}} = \frac{3}{3\sqrt{2}}= \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2} $$

$$ \sqrt{32} + \sqrt{50} = 4 \sqrt{2} +5 \sqrt{2} = 9 \sqrt{2} $$

といった平方根の計算も一瞬で解くことができるようになります。

NEXT→中学数学「平方根」のコツ③ 素因数分解／ルートを簡単にする計算