前回につづいて、作図のコツです。
今回は「角の二等分線」と「垂線」の応用範囲を整理していきます。
ついでに「正三角形」もやっつけます。
応用範囲はぜんぶで11項目。
これらを頭に入れることで、どんな難問が出ても解けるようになります。
では、前回同様に高校入試過去問をふんだんに使って、みていきましょう。
[中学数学「平面図形」の記事一覧]
- 垂直二等分線を使った作図
- 角の二等分線、垂線、正三角形を使った作図
- 高校入試問題を解いてみよう
- 図形の移動
- 円とおうぎ形
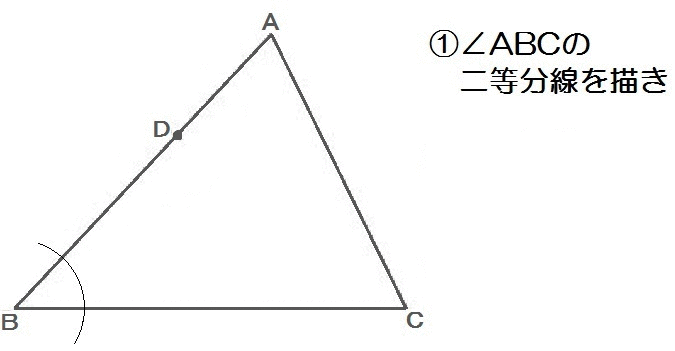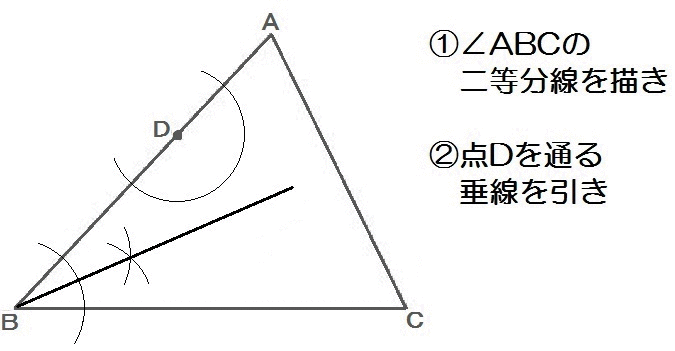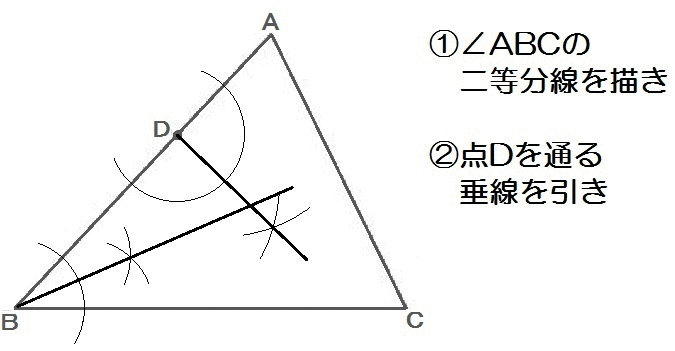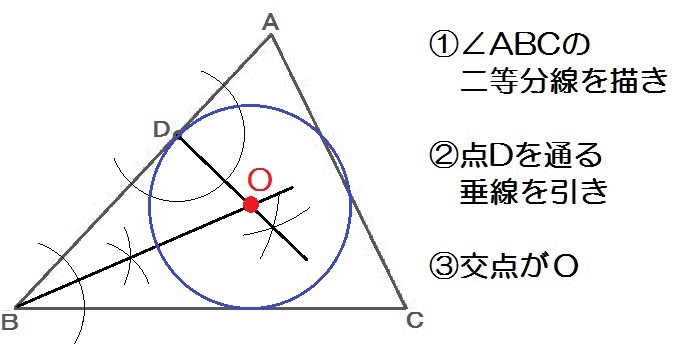
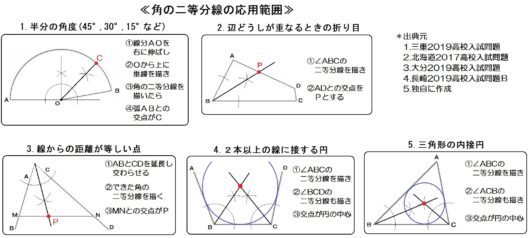
角の二等分線の定義
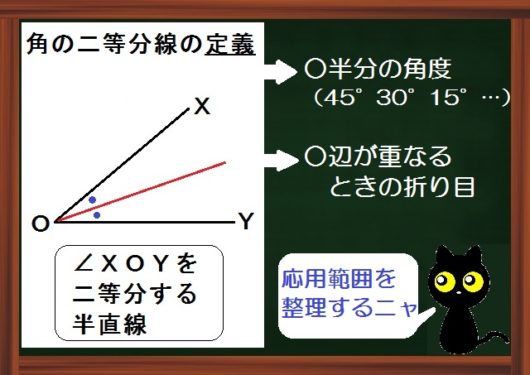
角の二等分線の定義は
角を二等分する半直線。
この定義から、
- 半分の角度
- 辺と辺が重なるときの折り目
という2つの応用範囲が出てきます。
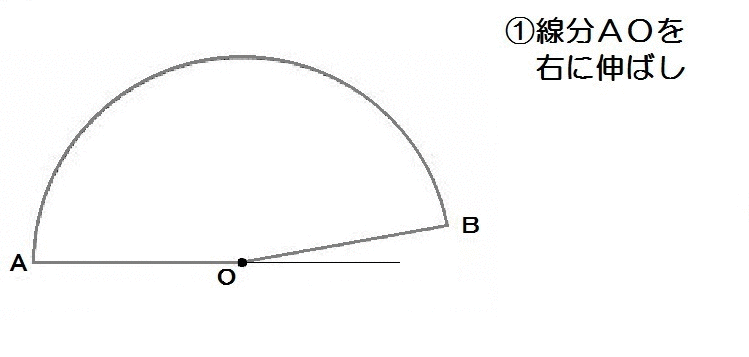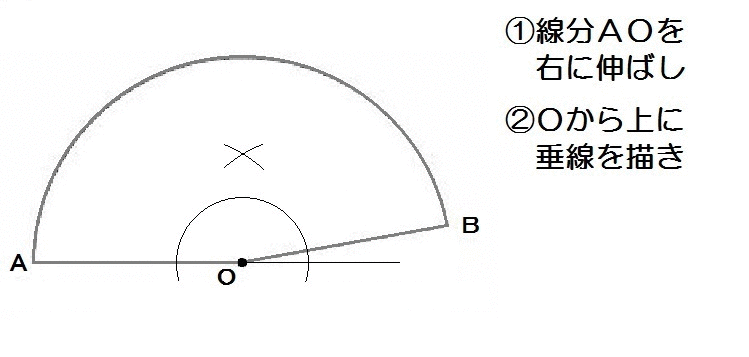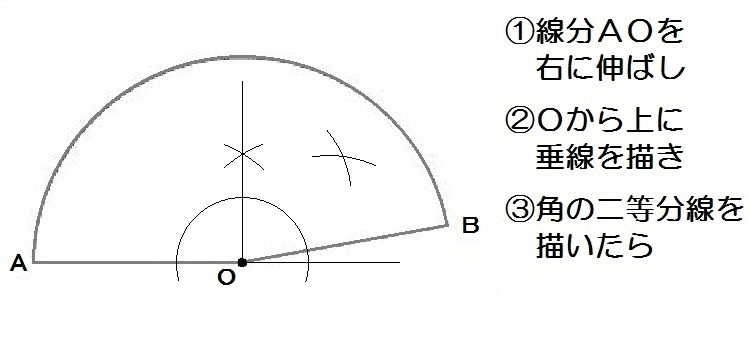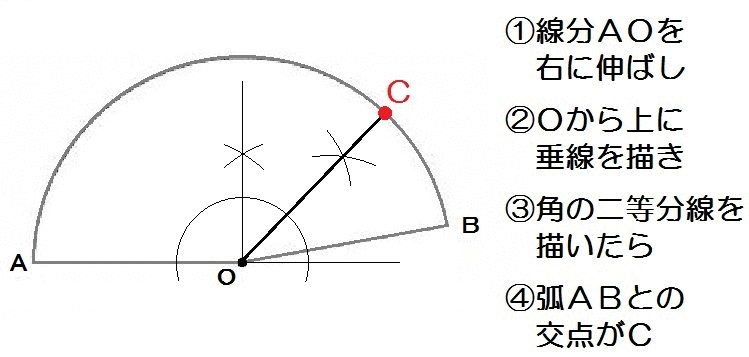
応用1:半分の角度
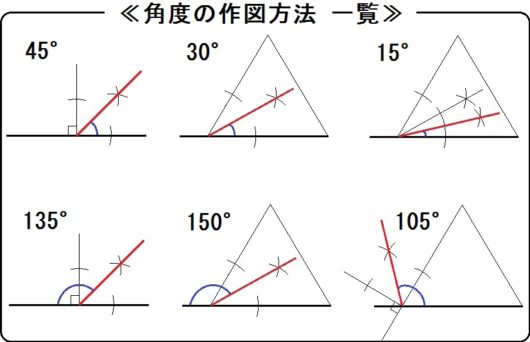
例題を解くまえに、角の二等分線をつかって作図できる角度をまとめます。
- 45° =90°(垂線)の半分
- 30° =60°(正三角形)の半分
- 15° =30°の半分
- 135° =180°-45° など
- 150° =180°-30° など
- 105° =60°+45° など
この6つの方法を押さえれば、角度の作図問題は難しくありません。
上の図をみて、いま理解してください。
必要ならば定規とコンパスで実際に作図して、記憶に残してください。
*90°(垂線)と60°(正三角形)の作図についてはあとで説明します。
OKですか?
では、実際の解き方にいきましょう。
この問題は2019年度の三重県の過去問です。
まずは完成形をイメージしましょう。
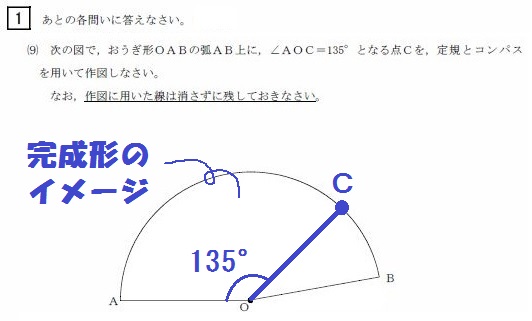
135° =180°-45° でしたね。
んで
45° = 90°(垂線)の半分でしたね。
よって解き方は以下のとおり。
2019三重1-9解答例
このように、角の二等分線なら半分の角度が作れるので、
45°,30°,15°,135°,150°,105°
という角度の作図ができるのです。
応用2:辺どうしが重なるときの折り目
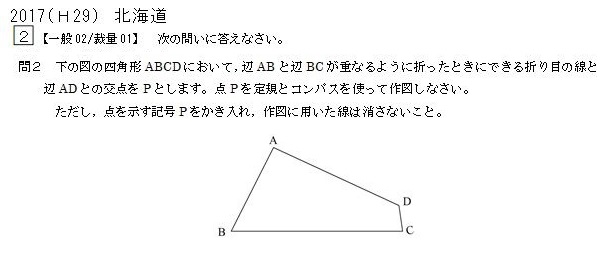
つぎに、2017年度北海道入試から。
辺ABと辺BCが重なるように折ったときの折り目なので、完成イメージはこんな感じ↓
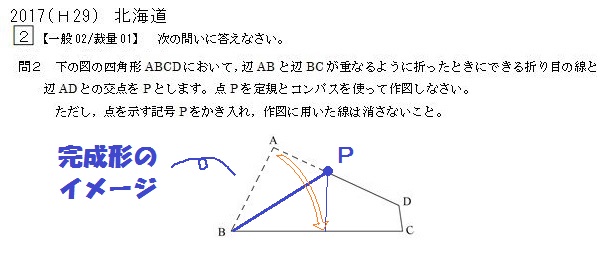
ここで、平面図形を折る問題で重要なコツをひとつ紹介します。
それは
「折る前と折った後の、辺や角は等しい」。
実際に手元に紙があったら折ってみてください。必ずそうなるから。まぁ当たり前ですね。
この問題でいえば、下図において
AB=A’B , AP=A’P
∠ABP=∠A’BP
となります。
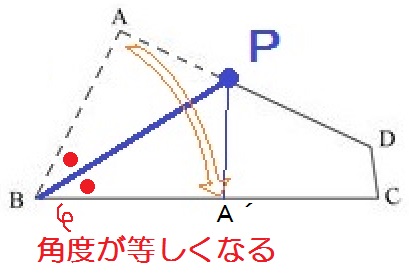
後者はつまり、BPが角の二等分線になるってこと。
なので、解き方は以下のとおり。
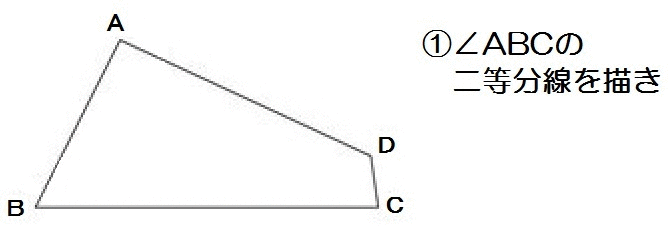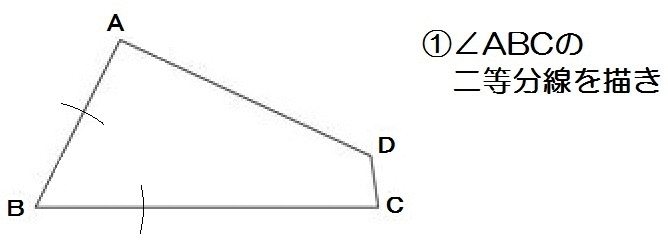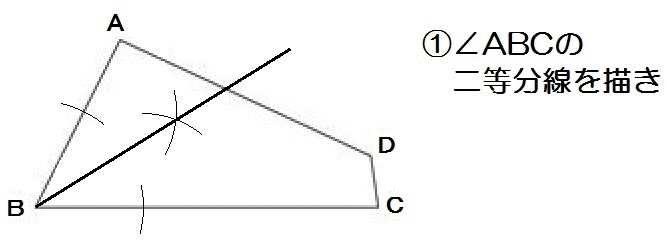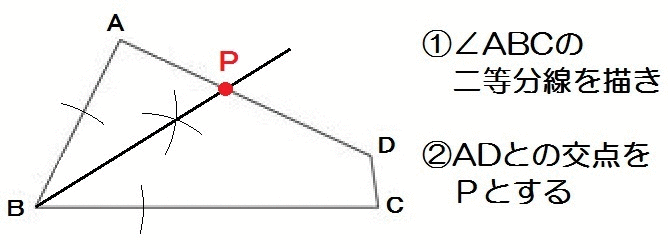
2017北海道2-2解答例
このように、辺どうしが重なるように折ったときの折り目の線にも、角の二等分線が使えるのです。
前回の記事で述べたことと合わせて、
- 点どうしが重なるときの折り目
→垂直二等分線 - 辺どうしが重なるときの折り目
→角の二等分線
と、セットで覚えておきましょう。
角の二等分線の特徴
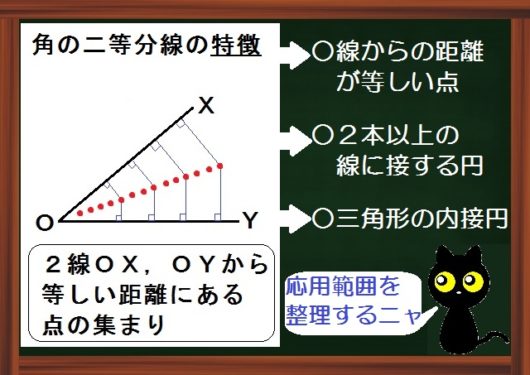
角の二等分線の特徴は
2直線から等しい距離にある点の集まり。
つまり角の二等分線上には、2線から等しい距離にある点が無数に並んでるってことです。
この特徴から、
- 線から等しい距離にある点の作図
- 線に接する円の中心の作図
- 三角形の内接円の作図
という3つの応用範囲が出てきます。
応用1:線からの距離が等しい
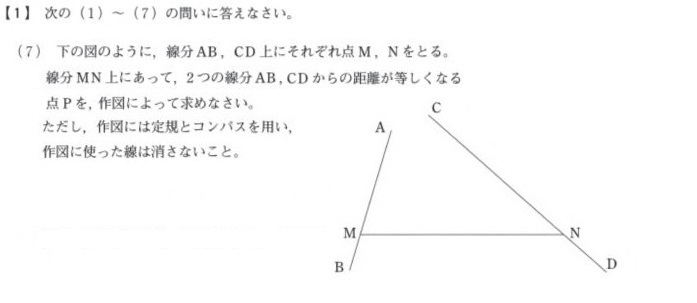
たとえばこの、大分の入試問題。
完成形のイメージはこんな感じですね↓

(点と直線の距離って、最短距離のことだから、図のように垂直になってる2本の青線が「距離」に当たります)
2つの線分ABとCDから等しい距離にあるんだから、やることは角の二等分線。
どこの角の?
ABとCDがつくる角です。
よって、解き方は以下のとおり。
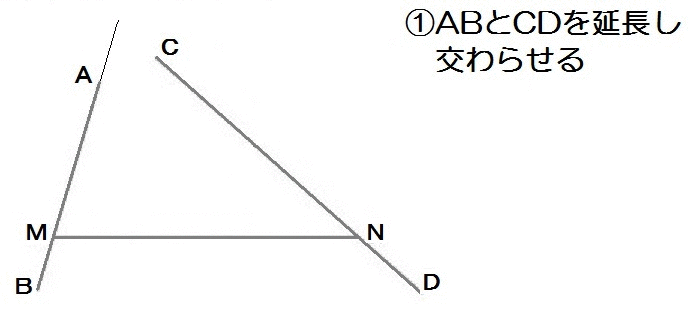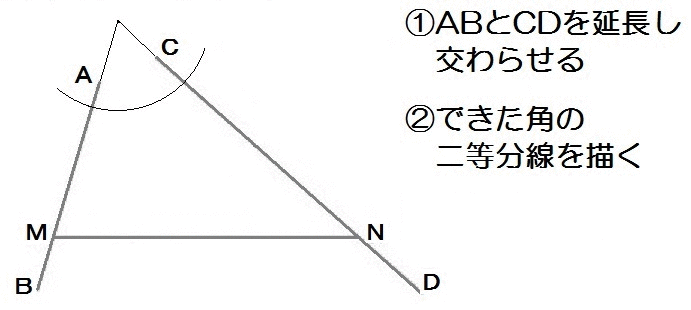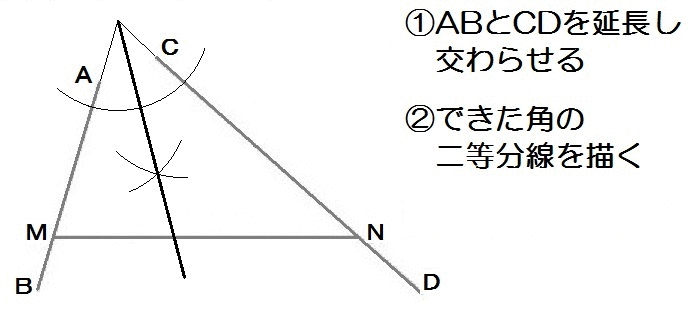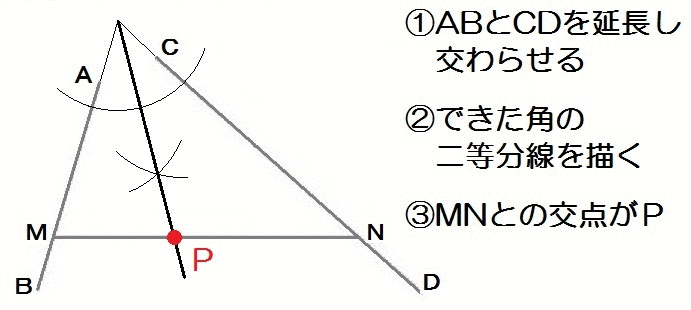
2019大分1-7解答例
このように、線(直線・線分・辺など)からの距離が等しい点の作図に、角の二等分線の特徴が使えます。
この問題は「2つの線分から等しい距離」だったので、角の二等分線は1本でOKでした。
もし「3つの線分から等しい距離にある」と出されたら、角の二等分線は2本書くことになります。
応用2:2本以上の線に接する円
つぎに、長崎のB問題から。
3つの線分すべてに接する円って、完成形はこんなイメージでしょうか↓

この完成イメージ図を見て気づいたと思いますが、
円と直線が接するところは垂直になります。
また、同じく気づきましたね。
円の半径はどれも同じ長さだと。
そして、先ほどの大分入試問題のイメージ図にありましたが、
点と直線の距離とは点からおろした垂線の長さのことです。
何が言いたいかというと、求める円の中心は3つの線分から等しい距離にある点だということ。
つまり、2本以上の線に接している円って、その中心は線からの距離が等しいんです。
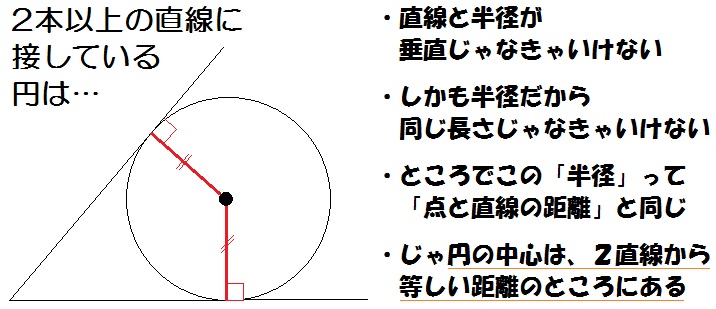
このあたりのことはすぐ後の「垂線」項目でも解説します。
ちょっと複雑だけど、大事な内容なんで、よく読んで理解してください。
さて、3つの線分から等しい距離にある点を作図しましょう。
つまり線分ABとBCからの距離が等しくて、線分BCとCDからの距離も等しいトコロ。
「2線から等しい距離にある点の集まり」という、角の二等分線の特徴が使えますね。
解き方は以下のとおり。
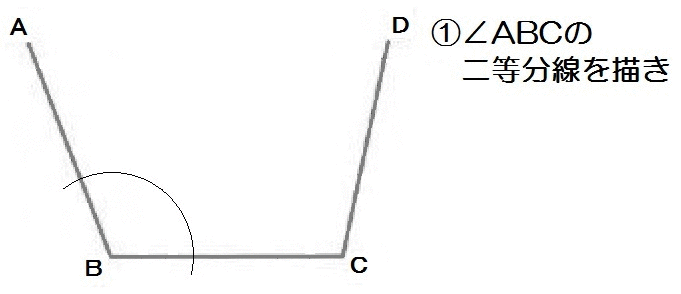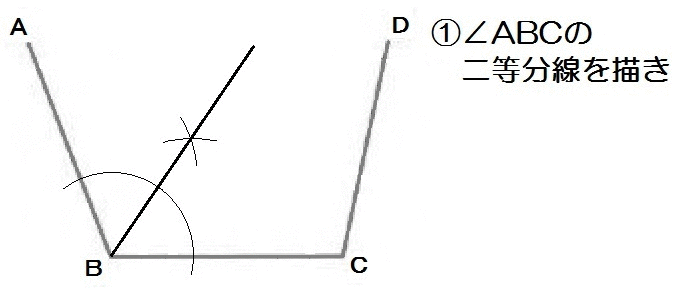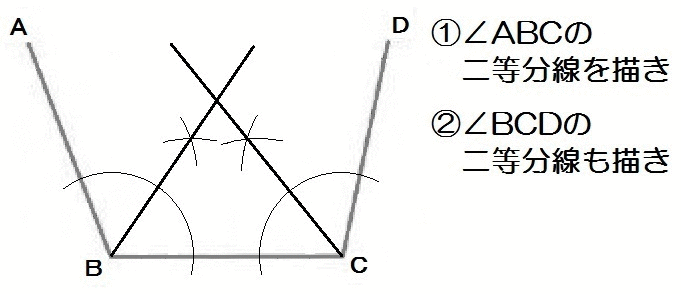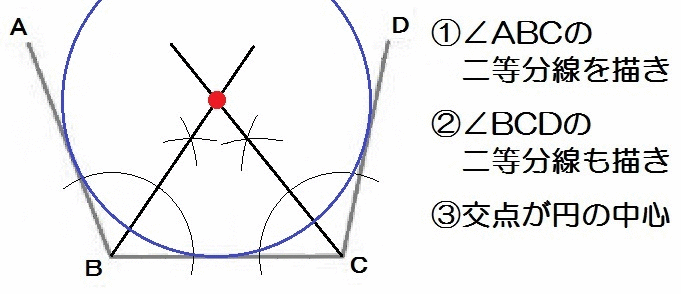
2019長崎B1-8解答例
このように、2本以上の線(直線・線分・辺など)に接する円の中心も、角の二等分線をつかって作図できるのです。
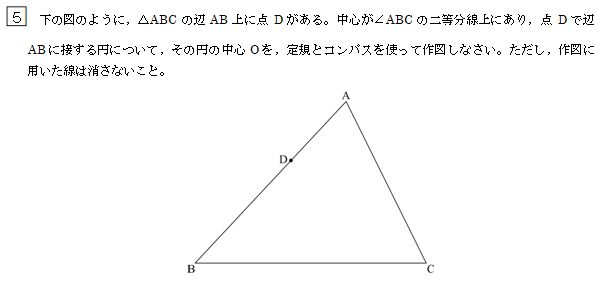
応用3:三角形の内接円
この「応用2:線に接する円」の考え方が理解できたら、以下の問題も解けます。
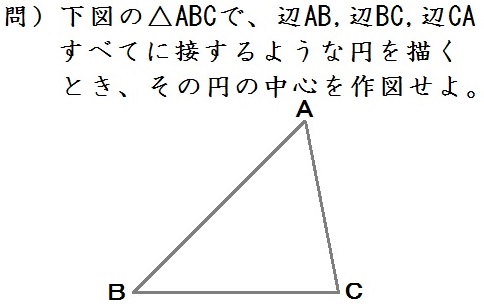
ちょっと入試問題が見当たらなかったんで、作ってみました。
完成形のイメージはこんな感じですね↓
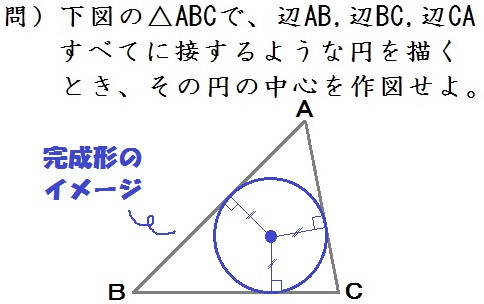
もうわかるでしょう。
角の二等分線を2本描けばいいと。
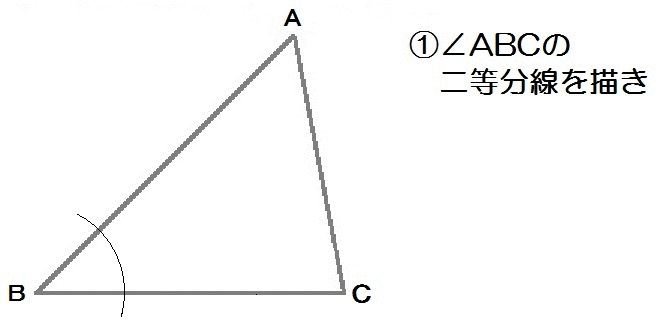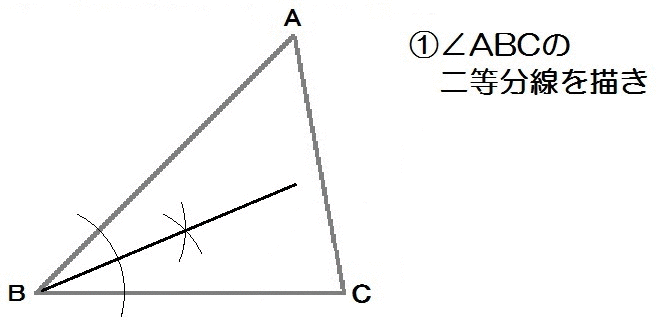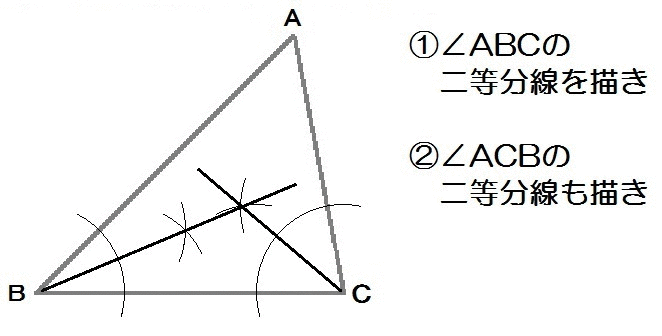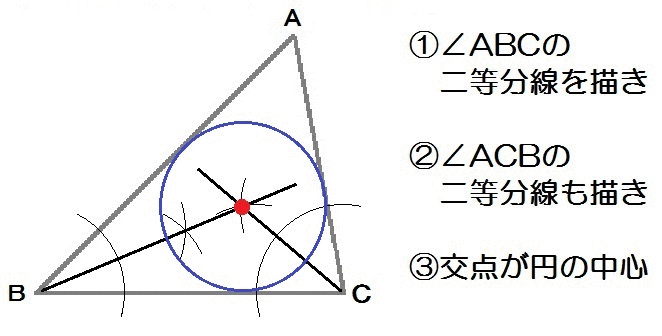
ちなみに。
こんな三角形に囲まれた円を「三角形の内接円」といいます。
なので、たとえば「三角形の内接円の中心を求めよ」と言われても、やることは同じ。
角の二等分線を2本描いて求めましょう。
以上、角の二等分線の応用範囲5つでした。
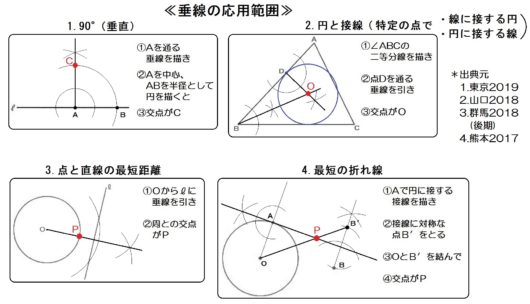
垂線の定義

つづいて、垂線の定義および特徴をおさえて、それぞれの応用範囲も整理します。
まず垂線の定義とは
垂直な線。
当たり前のこの定義から、
- 90°(垂直)の作図
- 円と接線の作図
という2つの応用範囲が出てきます。
応用1:90°の作図
この問題は2019年度の東京都の過去問です。
まず完成形をイメージしましょう。

Aを通る垂線を引いて、AB=ACとなるような点Cを取ればいいですね。
よって解き方は以下のとおり。
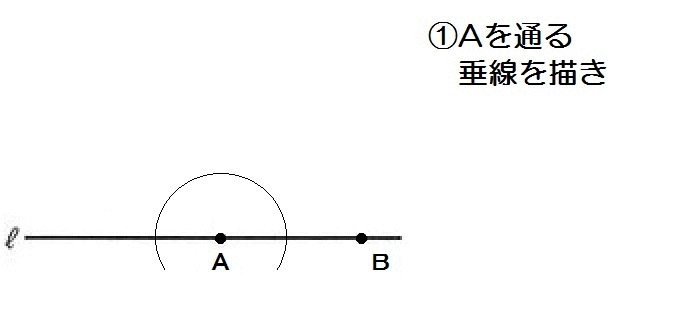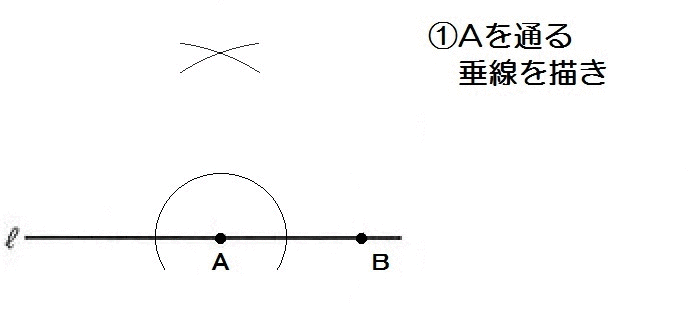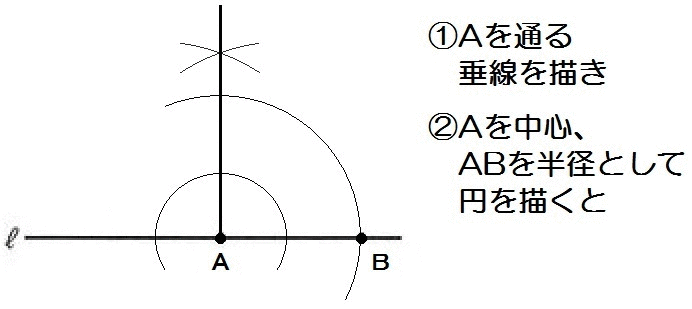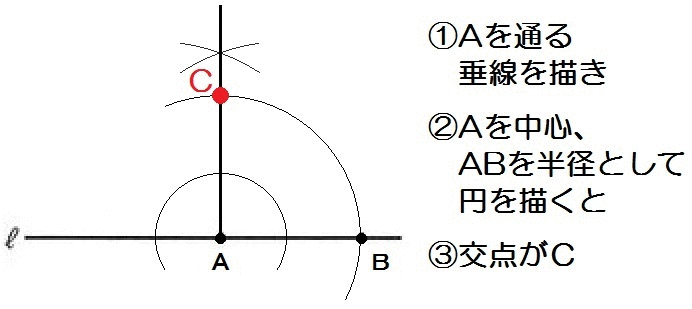
2019東京1-9解答例
このように、90°(垂直)の作図は垂線が使えます。
応用2:特定の点で接する円や線
つづいてこの、2018年度山口の過去問。
問題をよく読んで完成形をイメージすると、こんな感じ↓
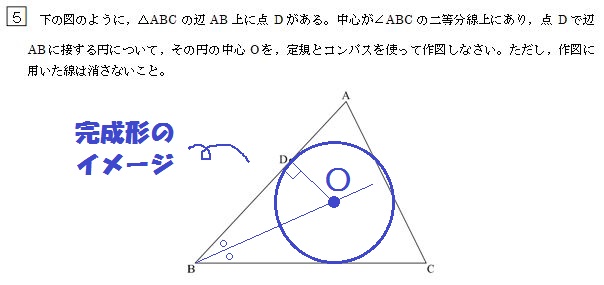
「角の二等分線の特徴:応用2」でも言いましたが、
円と直線が接するところは垂直になります。
つまり上図で、辺ABと半径ODが垂直になるんです。
よって、解き方は以下のとおり。
2018山口5解答例
このように、特定の点で線に接する円を作図するのに、垂線が応用できます。
ところで、上図の円Oにたいして、辺ABを「接線」といいます。
だから逆に、特定の点で円に接する線(=接線)を作図するのにも、垂線は使えます。
角の二等分線の特徴と似ていますが、
- 2本以上の線に接する円=角の二等分線
- 特定の点で線に接する円(または円に接する線)=垂線
というふうに区別して理解しましょう。
垂線の特徴
次に、垂線の特徴を用いた応用範囲です。
たびたび登場していますが、垂線の特徴とは
点と直線の最短距離のこと。
この特徴から、
- 点と直線の最短距離
- 最短の折れ線
という2つの応用問題がよく出題されます。
応用1:点と直線の最短距離
たとえばこの、2018年度の群馬(後期)入試問題。
完成形はこんなイメージですね↓

このイメージをみれば、最短となる点Pは、
中心Oから直線ℓまでの最短距離の途中にある、
ということがわかります。
よって、解き方は以下のとおり。
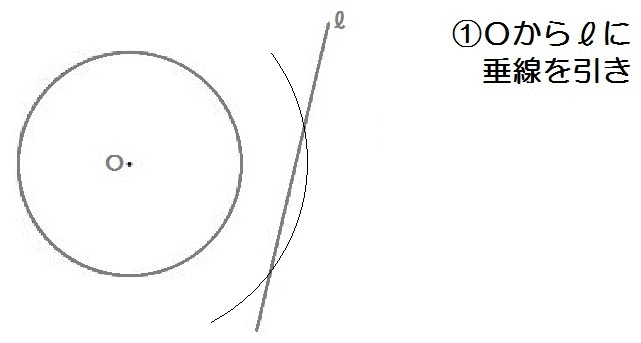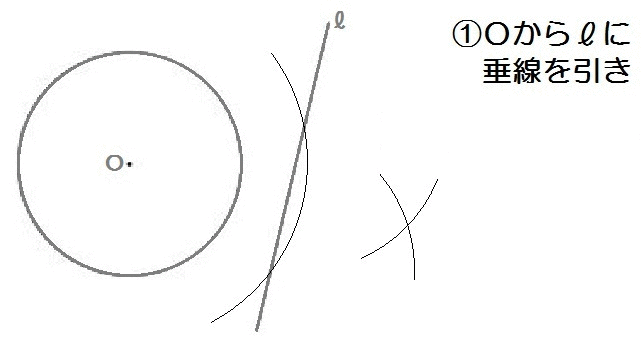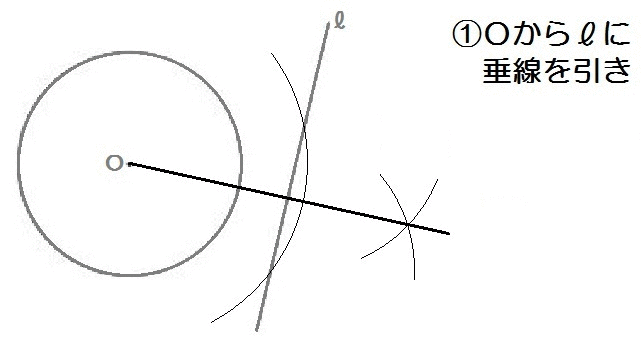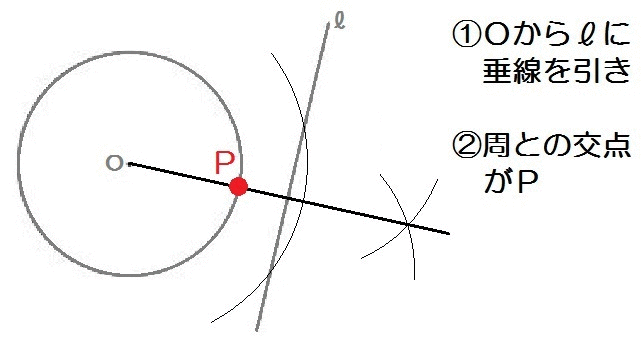
2018群馬1-8解答例
このように、点と直線の最短距離という問題に、垂線の作図が応用できるのです。
応用2:最短の折れ線
つづいて、2017年度の熊本の過去問です。
ちょっと難問ですが、とりあえず問題をよく読んで完成形をイメージしましょう。
「Aを接点とする円Oの接線」上にあって、
「OP+PBが最小となる点P」なので、
こんな感じ↓

接線はもう作図できますね。
特定の点Aで円に接する線なので、垂線を使います。
そのあと、OP+PBという折れ線の長さが最小となる点Pを求めます。
ここでコツ。
「折れ線の長さが最短」と言われたら
- どっちかの点を線対称移動させて
- 2点を結んで
- 線との交点が最短となるトコロ
という手順で作図できます。

「最短の折れ線」作図方法
なぜこれで最短の折れ線となるのか?
上図をみればわかりますね。
PB=PB’ となるので、
AP+PB = AP+PB’ 。
じゃAP+PB’が最短となるのは、まっすぐ結んだトコロだから。
この考え方を使って、2017熊本過去問も解けます。
解答例は以下のとおり。
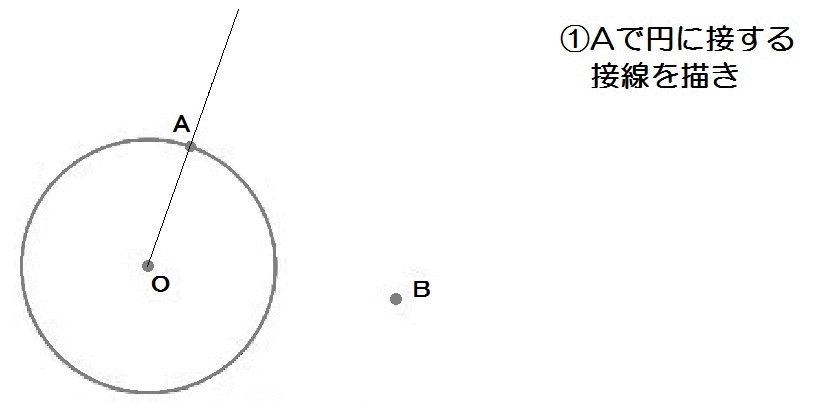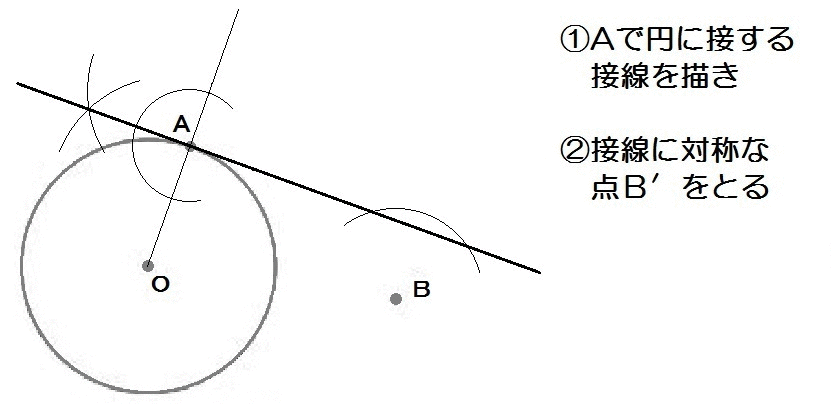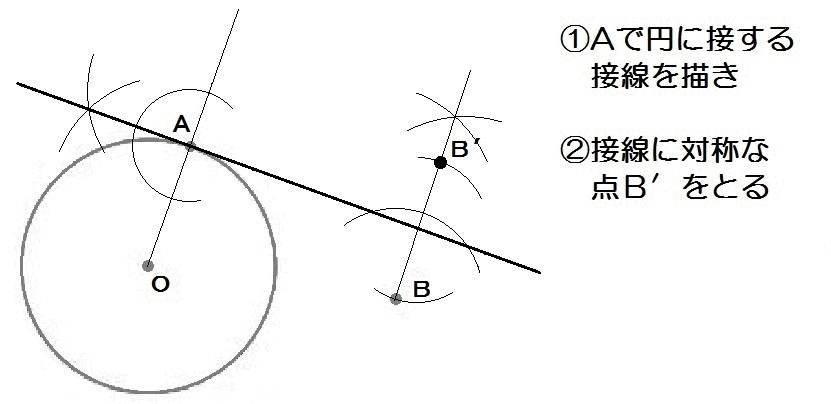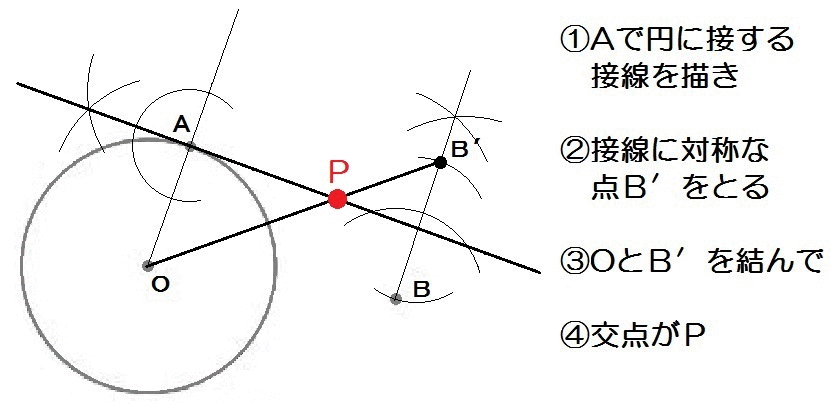
2017熊本2-5解答例
ちなみに点Bの線対称移動は、垂線を描いたあと交点にコンパスの針をおいて同じ長さで上側にピッとやればできます。
詳しくは平面図形④ 図形の移動にて
このように、最短の折れ線を作図するときにも、垂線が利用できるのです。
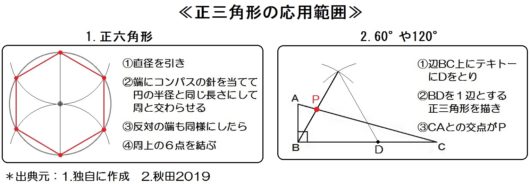
正三角形
ここまで
角の二等分線の定義・特徴から5つ、
垂線の定義・特徴から4つ、
計9つの応用範囲をみてきました。
最後に、正三角形の応用範囲も2つ、まとめときます。
応用1:正六角形
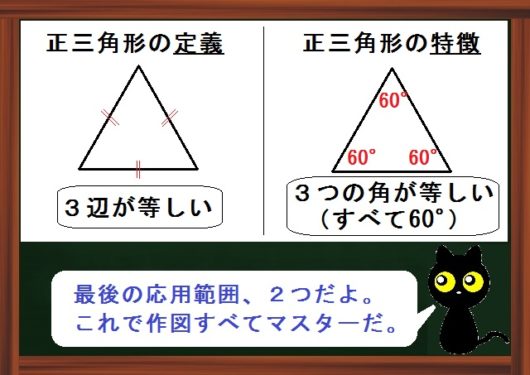
正三角形の定義は
3辺が等しい三角形です。
この定義から、たとえば
などの問題が出されます。
なぜ正六角形か?
完成形をイメージしてみればわかります。
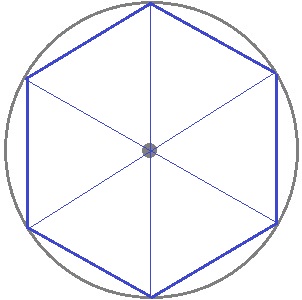
対角線を引くと、正六角形のなかには正三角形が6つあることがわかりますね。
だから、以下のような方法で正六角形を作図することができます。

この方法は、正三角形の「3辺の長さが等しい」という定義を使ったものです。
このように、正三角形の定義から、正六角形を作図することができるのです。
応用2:60°,120°の作図
正三角形の特徴は
3つの角が等しい(すべて60°)。
この特徴から、60°、120°などの作図ができます。
たとえば、2019年度の秋田入試問題。
30°の作図はこの記事の冒頭でやりました。
角の二等分線を使って、正三角形の半分とやってもいいです。
ただこの問題、すでに90°が与えられています。
つまり、∠PBC=90°-30°=60°ってこともわかる。
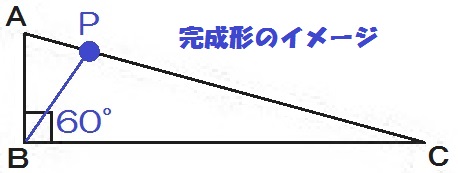
よって、正三角形の特徴を使って、以下のように解くこともできます。

2019秋田1-11解答例
もちろん、BCをそのまま1辺として正三角形を描いてもいいです。
とにかく、60°や120°(=180°-60°)の作図ときたら、正三角形が利用できるということです。
まとめ

以上、2回にわたって
- 垂直二等分線
- 角の二等分線
- 垂線
- 正三角形
という4つの作図から、どんな応用範囲が導かれるのか、みてきました。
まとめると、
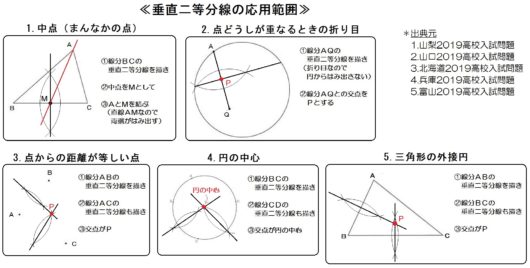
【垂直二等分線の応用範囲】
- 中点(まんなかの点)
- 点どうしが重なるときの折り目
- 点からの距離が等しい点
- 円の中心
- 三角形の外接円
【角の二等分線の応用範囲】
- 半分の角度(45°,30°,15°など)
- 辺どうしが重なるときの折り目
- 線からの距離が等しい点
- 2本以上の線に接する円
- 三角形の内接円
【垂線の応用範囲】
- 90°(垂直)
- 特定の点で線に接する円
(または特定の点で円に接する線) - 点と直線の最短距離
- 最短の折れ線
【正三角形の応用範囲】
- 正六角形
- 60°や120°
これら計16コが、中学一年生で出てくる作図問題のすべてです。
これら16コの知識を持っていれば、どんな難問に出合っても解くことができます。
そのことを証明するために、次回では高校入試過去問から難問をよりすぐって出題します。
一緒に解いていきましょう。
→中学数学「平面図形」のコツ③ 作図の高校入試問題を解いてみよう
[中学数学「平面図形」の記事一覧]
- 垂直二等分線を使った作図
- 角の二等分線、垂線、正三角形を使った作図
- 高校入試問題を解いてみよう
- 図形の移動
- 円とおうぎ形








コメント
返信ありがとうございます。
・また円Oの周上で直線ℓにもっとも近いのは、直線m上にあるP。
ここが、どうもよくわかりません。
当たり前のことかもしれませんが。
2018群馬県(後期)の問題ですが、
どうして、最短となる点Pは、 中心Oから直線ℓまでの最短距離の途中にある、といえるのでしょうか?
(なんとなくはわかりますが、どうしてと聞かれると、うまく説明できません)
たとえば、
・直線ℓに平行な円Oの接線mを引く(ℓとmは同じ側にあるものとする)。
・その接点をPとすると、OP⊥m。
・また円Oの周上で直線ℓにもっとも近いのは、直線m上にあるP。
・よって最短となる点Pは、中心Oから直線ℓまでの距離上の途中にある。
以上の内容を図で示せば説明のひとつになるかと思います。