中学数学のつまずき解消をめざすこの連載。
今回から連立方程式の文章題に入ります。
方程式文章題の解き方についてはすでに「中1 一次方程式の文章題」で9回にわたり詳しく解説しました。
が、ここでもういちど、やり方はわかるけど実際に解こうとするとできないとなるのはなぜか、そして解決策は何か、原因とコツを掘り下げていきます。

1回目は、あらゆる問題に当てはまる基本。
そして最も多くの中学生がつまずく点を取り上げます。
それは「文章を読んでそこから方程式を立てる」という所。
あのごちゃごちゃした日本語を読んで、それを等式っていう数学の形になおす、そこんところが未だによくわからないし、できないんだよね…。
こういう場合の原因と解決方法をまとめます。
連立方程式でつまずいているすべての人にご参考ください。
なお、この記事を最後まで読めば、高校入試で実際に出た問題が解けるようにしてあります。
立式でつまずく原因は3段階ある

文章を読んで方程式を立てる。
これができるためには、じつは3つの段階をすべてクリアしている必要があります。
- 「数量を文字で表す」段階
- 「等しい関係を見つける」段階
- 「日本語の文章を数式になおす」段階
1の「数量を文字で表す」段階でつまずいている中学生というのは、たとえば以下の問題に困る人のことです。
例1)次の数量を表す式を書きなさい。
(1)100円のドーナツを \(x\) 個と、150円のカップケーキを \(y\) 個売ったときの合計の売上
(2)ある動物園の入場者が金曜日は \(x\) 人、土曜日は \(y\) 人、日曜日は金曜の3倍だったとき、3日間の入場者の合計
(3) \(x\)gと \(y\)gを合わせた重さの2倍より10g少ない
(1) \(100x+150y\) (円)
(2) \(x+y+3x\) (人)
(3) \(2(x+y)-10\) (g)
2の「等しい関係を見つける」段階でつまずいている中学生というのは、例えば以下の問題を難しく感じる人のことです。
例2)次の数量の関係を等式で表しなさい。
(1) \(x\) 人と \(y\) 人と5人を合わせると33人である。
(2) \(y\) の3倍は \(x\) の2倍より12大きい。
(3) \(x\) 枚の4倍から \(y\) 枚を引くと \(x\) 枚の半分に等しい。
(1) \(x+y+5=33\)
(2) \(3y=2x+12\)
(3) \(4x-y= \frac{1}{2}x\)
3の「日本語の文章を数式になおす」段階でつまずいている中学生というのは、たとえば以下の問題ができない人のことです。
例3)次の文章を読んで連立方程式を作りなさい。
(1)異なる2つの数があり、その和は18で、一方の数は他方の数の3倍より2大きい。この2つの数を求めよ。
(2)A,B,Cという班がある。3つの班の人数を合わせると33人である。またAの人数は5人で、Bの人数の2倍からCの人数をひくと、Aの人数に等しい。B,Cの班の人数をそれぞれ求めよ。
\begin{eqnarray} \mbox{(1)} \left\{ \begin{array}{l} x+y = 18 \\ x = 3y+2 \end{array} \right.\end{eqnarray}
\begin{eqnarray} \mbox{(2)} \left\{ \begin{array}{l} 5+x+y = 33 \\ 2x-y = 5 \end{array} \right.\end{eqnarray}
あなたのつまずきはどの段階ですか?
それによって、解決策もちがってきます。
以下、段階別に原因と解決方法をくわしく紹介していきますが、まずは自分がどこでつまずいているのかハッキリさせることが重要です。
そのうえで、
1段階目の人は「数量を文字で表す」コツ(すぐ下)へ。
2段階目の人は「等しい関係を見つける」コツへ。
3段階目の人は「文章を数式になおす」コツへ。
それぞれ飛んでください。
そのあと「入試問題を解いてみよう」と、「まとめと4番目の原因」を読みすすめてください。
なお、立式の基本はできてるという人は次の記事へどうぞ。
→中学数学「連立方程式」文章題の解き方②【整数、過不足問題など】
数量を文字で表すコツ

連立方程式文章題の基本問題において、「数量を文字で表す」段階でつまずく原因は、中1の文字と式④ 数量の表し方でも書きましたが、4つあります。
- 国語力の欠如
- 単位を揃えられない
- 割合・速さ・平均・面積の求め方を忘れている
- 文字が入ると式を立てられない
解決方法
このうち
- 国語力の欠如
は、長期間かけて読解力を上げるしか方法がありません。
上記の問題でも「何を言っているのかわからない」という中学生は、まずスマホやタブレット、ゲーム機を手放すこと。
そして絵本やライトノベルなど、自分がスラスラ読めるものから読書を始めましょう。
また、
- 単位を揃えられない
- 割合・速さ・平均・面積の求め方を忘れている
という2つは、単位変換の仕方や割合・速さ・平均・面積の求め方を復習することで解決します。
詳しい復習方法は以前の記事に載っているので、そちらを参照してください。
→中学数学「文字と式」でつまずく原因と解決法④ 数量の表し方
そして、
- 文字が入ると式を立てられない
つまり何を言っているかはわかるけど、文字になると数式を作れない中学生には、
- 図を描いてイメージし
- それでもダメなら文字の代わりに具体的な数字を入れて
- 何算するか考える
これらのコツが有効です。
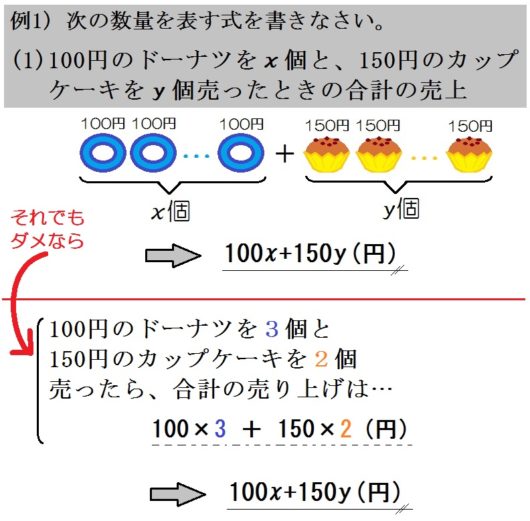
たとえば例1の(1)はこんな感じ↓
とくに大切なのは、 文字の代わりに適当な数字を入れたあと、「300円って何算で出したっけ?」「合計600円って、何算で出したっけ?」などと意識することです。そうすれば \(100 \times 3\) などの式が立つようになるでしょう。
図を描いてイメージし、それでもダメなら文字の代わりに具体的な数字を入れて、何算するか考える。
このコツを使って、数量を文字で表すことに慣れていきましょう。
等しい関係を見つけるコツ

連立方程式文章題の基本問題において、「等しい関係を見つける」段階でつまずく原因は2つあります。
- 基本の3パターンがしっかり頭に入ってない
- 日本語の表現がひねってあると思考停止する
解決方法
等しい関係は基本的に以下の3パターンに集約できます。
①「○と△を合わせると□」
→ ○+△=□
②「○は△より□小さい(大きい)」
→ ○=△ー□
→ ○=△+□
③「○は△と等しい」
→ ○=△
この3パターンを押さえること。
そのうえで、類似の日本語表現をたくさん知ること。
これが「等しい関係を見つける」コツです。
たとえばパターン①なら↓
- \(x\) 個と \(y\) 個と \(3x\) 個の合計は \(17\) 個。
→ \(x+y+3y=17\) - \(5\) と \(x\) の和が \(y\) 。
→ \(5+x=y\) - \(4000\)gの小麦粉をすべて使って、\(40\)gのドーナツを \(x\) 個、\(30\)gのカップケーキを \(y\) 個つくった。
→ \(40x+30y=4000\)
パターン②なら↓
- \(x\) を \(5\) 倍しても \(y\) に \(8\) 足りない。
→ \(5x=y-8\) - \(3776\)mは \(x\)mよりも \(y\)mだけ高い。
→ \(3776=x+y\) - 男子の人数 \(x\) 人は女子の人数 \(y\) 人より \(4\) 人少ない。
→ \(x=y-4\)
パターン③なら↓
- \(x\) と \(y\) の積が \(40\) である。
→ \(xy=40\) - \(x\) から \(y\) を引いた差は \(30\) になる。
→ \(x-y=30\) - \(4\)gの分銅 \(x\) 個は \(7\)gの分銅 \(y\) と釣り合う。
→ \(4x=7y\)
等々、いろんな類似表現があります。
このようにいろいろな表現をされても、すべてどれかのパターンで等式を立てることができるんだ。
ここでつまずいている生徒はそう思って、練習に励みましょう。
文章を数式になおすコツ

連立方程式文章題の基本問題において、「日本語の文章を数式になおす」段階でつまずく原因、これは1つです。
- 文中の未知数を \(x , y\) で読み替えられない
解決方法
つまり何が \(x\) で何が \(y\) なのか明確じゃないまま、文章を読んでうーんと悩んでる。
こういう状態の中学生が実に多いのです。
こうした生徒には、以下2つのコツが有効です。
- 一行目に「~を \(x\) 、~を \(y\) とする」と必ず書く
- 文中のことばを \(x , y\) に書き替える
連立方程式文章題を解く手順は以下のとおりです。
①求めるものを \(x , y\) とする
②文章を読んで連立方程式を立てる
③その連立方程式を解く
④問題に合っているか確かめる
これは一次方程式文章題①で書いた内容とほぼ同じ。
しかし中2になっても、最初の手順を飛ばす生徒をかなり見かけます。
例題3の問題でいえば、
(1)「異なる2つの数を \(x , y\) とする。」
(2)「B班の人数を \(x\) 人、C班の人数を \(y\) 人とする。」
などと、一行目に必ず書くこと。
これを守るだけで、解きやすさがぐっと変わります。
そのうえで、問題文のことばを \(x ,y\) で書き換えてみる。
例題3なら、こんな感じ↓
こうすれば、
\begin{eqnarray} \mbox{(1)} \left\{ \begin{array}{l} x+y = 18 \\ x = 3y+2 \end{array} \right.\end{eqnarray}
\begin{eqnarray} \mbox{(2)} \left\{ \begin{array}{l} 5+x+y = 33 \\ 2x-y = 5 \end{array} \right.\end{eqnarray}
と連立方程式が立つはずです。
- 一行目に「~を \(x\) 、~を \(y\) とする」と必ず書く
- 文中のことばを \(x , y\) に書き替える
この2つのコツで、日本語の文章を方程式になおしていってください。
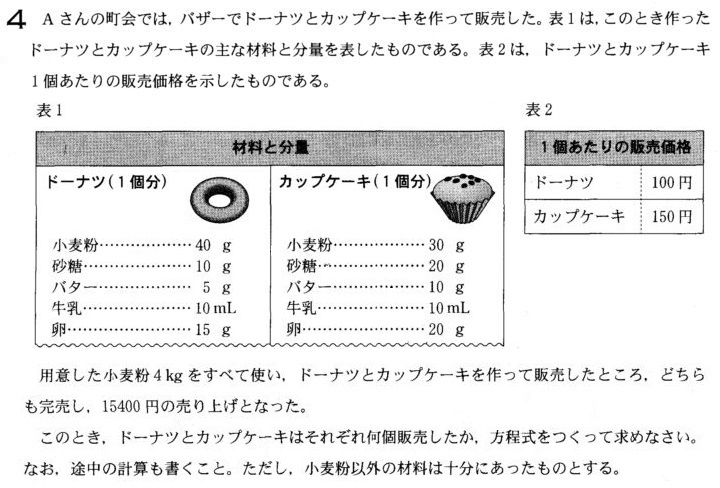
入試問題を解いてみよう

以上、数量を表すコツ、等しい関係を見つけるコツ、文章を数式になおすコツをお伝えしてきました。
ここまで読んだなら、以下に出す高校入試問題すべて解けるはずです。
上から順に、鹿児島県・佐賀県・石川県の2019年度高校入試より、連立方程式文章題部分の抜粋です。
ぜひチャレンジしてみてください。
なお解答は問題の一行下をドラッグ反転、質問はコメント欄からどうぞ。
まとめと4番目の原因

この記事の内容をまとめます。
立式でつまずく原因と解決方法
●中2数学 連立方程式の文章題。
「文章を読んで方程式を立てる」ところでつまずく場合、そのつまずきは3段階ある。
- 「数量を文字で表す」段階
- 「等しい関係を見つける」段階
- 「日本語の文章を数式になおす」段階
●1.でつまずく原因は4つ。
- 国語力の欠如
- 単位を揃えられない
- 割合・速さ・平均・面積の求め方を忘れている
- 文字が入ると式を立てられない
このうち国語力の欠如は読書で読解力を鍛えるしかない。また単位や割合・速さ・平均・面積は求め方を復習する。
そして4番目の場合は
図を描いてイメージし、それでもダメなら文字の代わりに具体的な数字を入れて、何算するか考えるというコツが有効。
●2.でつまずく原因は2つ。
- 基本の3パターンがしっかり頭に入ってない
- 日本語の表現がひねってあると思考停止する
よって、
①「○と△を合わせると□」
→ ○+△=□
②「○は△より□小さい(大きい)」
→ ○=△ー□
→ ○=△+□
③「○は△と等しい」
→ ○=△
この3パターンを押さえること。そのうえで、類似の日本語表現をたくさん知ること。
●3.でつまずく原因は
- 文中の未知数を \(x , y\) で読み替えられない
というもの。よって
- 一行目に「~を \(x\) 、~を \(y\) とする」と必ず書く
- 文中のことばを \(x , y\) に書き替える
というコツが有効。
4番目の原因とは
ただ、連立方程式の文章題で「式が立てられない」となる原因はこれだけじゃありません。
整数や自然数、平均や過不足、道のりや割合といったその問題特有の式の立て方を知らない。
この4番目の原因もあるんです。
そこで次回からは、問題パターン別に解き方を解説していきます。
池の周りを回る問題とか、列車が出てくる文章題になると、できなくなる…。
3桁の整数とか、食塩水の問題とかが苦手…。
こんな場合にお役立てください。
2回目→中学数学「連立方程式」文章題の解き方②【整数、過不足問題など】
















コメント
連立方程式の文章題は、基本的には、一次方程式(一元方程式)の問題に置き換えることができますよね(逆に言えば、1年生のときは、本来連立方程式として扱うべき問題を、工夫して?一次方程式として解いている、ともいえる)。
つまり、文字を1つだけ使うか、2つ使うか、の違いだけで、どちらの解き方でも、答えを出すことは可能です。
(そのことに、多くの生徒は気づいていない)
その点、どのように指導されているのか、よろしければ教えてください。