三角比・三角関数について4回目の記事です。
前回「三角比の拡張」と「ラジアン」を解説したので、今回は三角関数のグラフについて解説します。
数Ⅱで習ったように、三角関数のグラフとは、たとえばこんなのでした↓
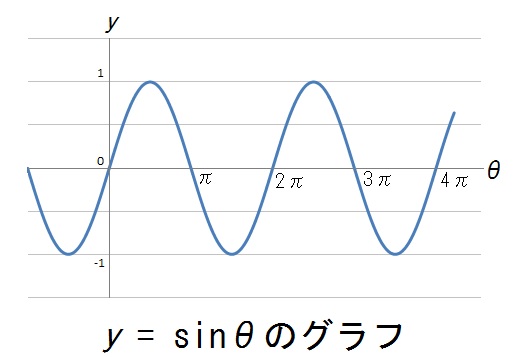
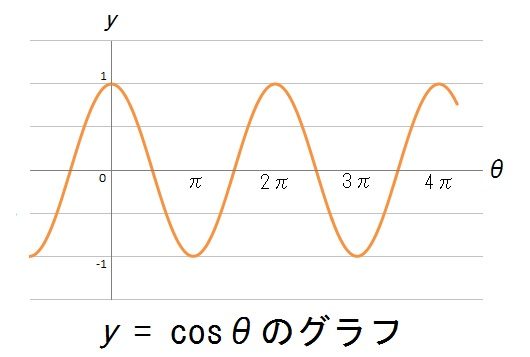
くわしい解説はのちほどするので、とりあえず「波みたいなグラフだな」「おんなじ形の波が周期的にくりかえしてるな」などと感じてもらえればけっこうです。
そんでじつは、このsinとcosのグラフを何回も足し合わせることで、どんな複雑なグラフでも表現できちゃうんです。
たとえばこんなの↓
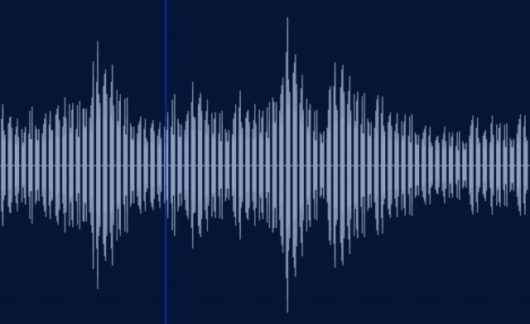
音波
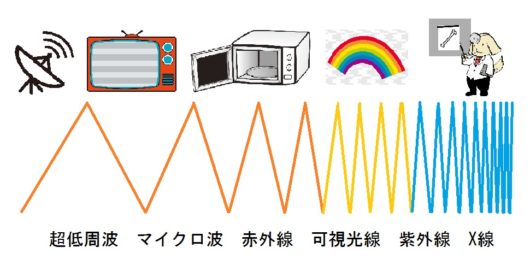
電磁波
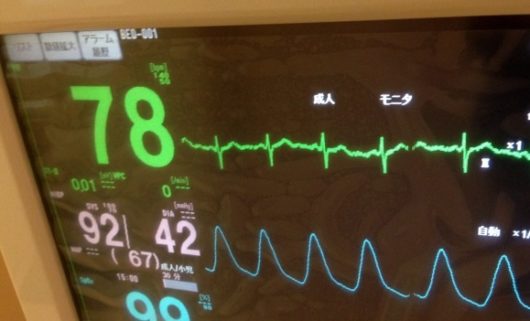
心電図
こうした音、電磁波をはじめとした技術への応用が、三角関数の役に立っている分野なんです。
そしてこの応用を可能にする道具が、「フーリエ級数」という数式なんです。
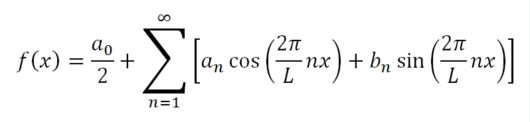
フーリエ級数
このフーリエ級数を、数Ⅱ・数Bまでの知識で理解すること。
これが今回のシリーズの最終目標です。
こまかな数学の話はおいといて、フーリエ級数がどんなものかイメージできれば、三角関数を学ぶ意味も実感できるでしょう。
ってことで、今回はフーリエ級数を理解するための準備として、三角関数のグラフを復習しましょう。
≪連載記事一覧≫
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)
スポンサーリンク
グラフの振幅
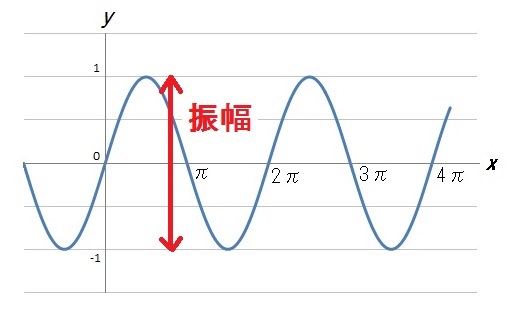
三角関数のグラフには「振幅」「周期」「平行移動」という3つの要素があります。
それぞれ数式とグラフの関係を見ていきましょう。
まずは基本のグラフを描く
まず基本となる \(y = \sin x\)、\(y = \cos x\) のグラフを描きます。
(\(θ\) を \(x\) に変えてますが、たんなる趣味です)。
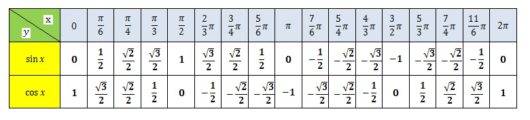
下表のように、代表的な角度をとって、それぞれの値をじっさいに計算します。
んで座標上にそれぞれの値をプロットすると、グラフが描けます。
(じっさいのグラフはエクセルでもっとこまかく値をとっています。エクセルで三角関数のグラフをかく方法はこちら)
できたグラフは、最初に掲げた図のように、波みたいなグラフになります。
このとき、波の最高点と最低点の幅のことを「振幅」といいます。
「しんぷく」と読みますが、まあ「ふれはば」と言ったほうがわかりやすいですね。
ちなみに音波の場合だと、この振幅は「音の大きさ」に相当します。
振幅は\(\sin x\) の係数によって変わる
ここで \(\sin x\) の係数をいろいろと変えてみましょう。
すると、振幅が変化することがわかります。
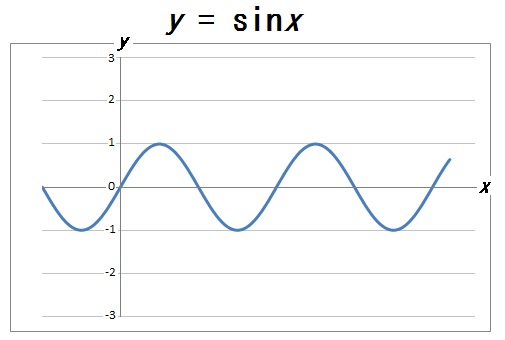
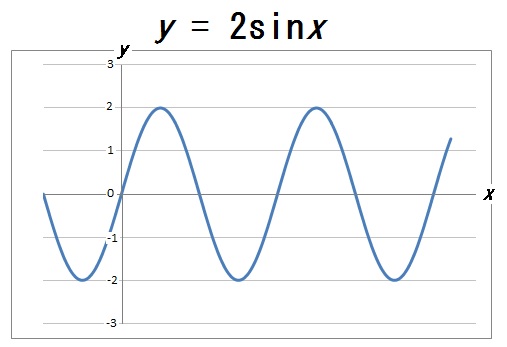


ここから、\(y =a\sin x\) の \(a\) の値をいろいろと変えることで、グラフの振幅を自由に操れることがわかります。
グラフの周期
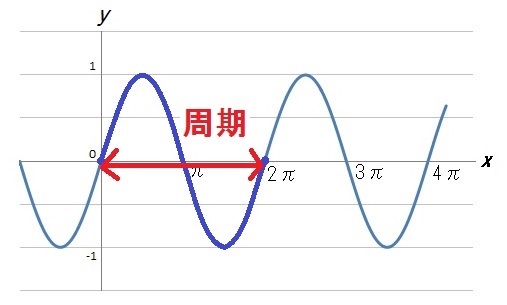
つぎに「周期」を解説します。
三角関数のように、グラフのなかでおなじ形がくりかえし現れるものを「周期関数」と呼びます。
このとき、基本となる形ひとつの横幅を「周期」といいます。
上図のように \(y = \sin x\) であれば、周期は「\(2π\)」です。
周期は \(x\) の係数によって変わる
ここで \(x\) の係数をいろいろと変えてみましょう。
すると、周期が変化することがわかります。
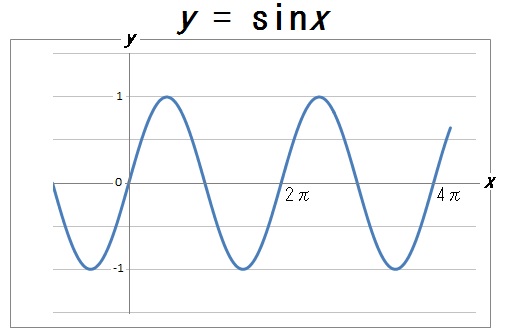
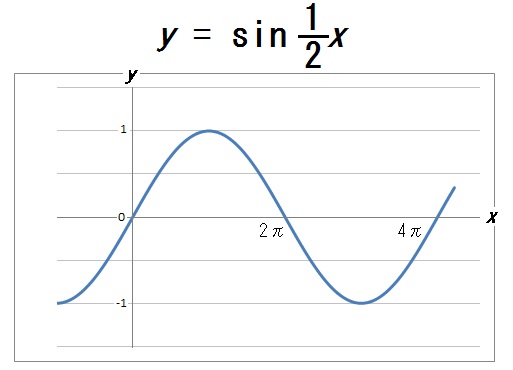
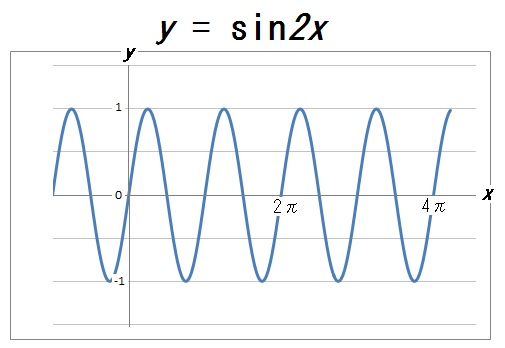
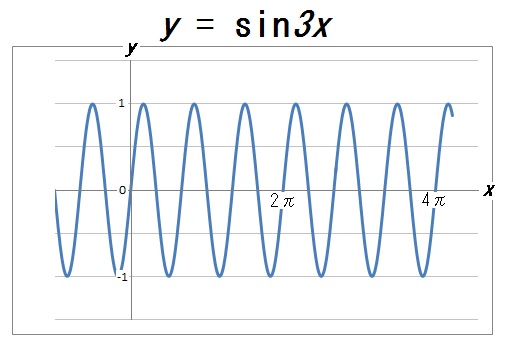
ここから、\(y =a\sin bx\) の \(b\) の値をいろいろと変えることで、グラフの周期も自由に操れることがわかります。
「周波数」と「周期」の関係
周期の長短は、音の場合でいえば「音の高さ」に相当します。
つまり周期が長いときには音が低く、周期が短いときには音が高くきこえます。
また電磁波の場合でいえば、周期の長短は「エネルギーの大きさ」に相当します。
つまり周期が長いときにはエネルギーが小さく、周期が短いときにはエネルギーが大きくなります。
なんでこんな話をするかというと、ここでついでに「周波数」と「周期」の関係も整理しとこうと思うからです。
「周波数」とは、ある一定範囲において周期がいくつあるかという数です。
ようするに、1秒間にグラフの基本の波が何個あるか、それを表した値なんです。
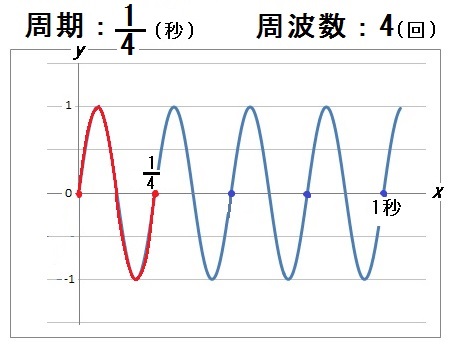
たとえば↑のようなグラフでは、周期は「\( \frac{1}{4}\)」です。
それにたいして周波数は、1秒間に基本の波が4個あるので、「4」になります。
ただ周波数は「Hz(ヘルツ)」という単位を使うので、正確にいえば「4Hz」です。
たとえばニッポン放送の周波数は「1242Hz」ですが(東京の場合)、これは1秒間に1242回の電気の波(電磁波)があるってことです。
そしてその波ひとつぶんの周期は「\(\frac{1}{1242}\) 秒」なんです。
*2020/1/27 ニッポン放送の周波数は「1242kHz」、よって周期は「「\(\frac{1}{1242000}\) 秒」でした、お詫びして訂正します。
以上からわかるとおり、「周期」と「周波数」とは逆数の関係になっています。
数式で表せば、$$(周期)= \frac{1}{(周波数)}、(周波数)= \frac{1}{(周期)}$$という関係です。
だから周期が短い(小さい)ほど、周波数は逆に多く(大きく)なるんです。
よって、周期の代わりに周波数という単位を使えば、周波数が大きくなるほど音も高くなる、エネルギーも大きくなる、となります。
つまり「周波数の大小」と「音の高低」と「エネルギーの大小」がぜんぶおんなじ関係になって、わかりやすいんです。
周波数という単位がよく使われるのも、こういう理由です。
以上、周期ついでに、周波数の話でした。
グラフの平行移動
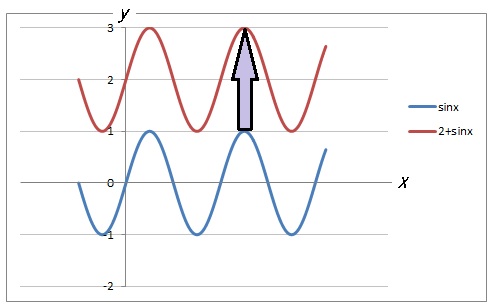
最後に、グラフの「平行移動」を解説します。
まあいままでと似たような話なんで、以下のグラフを見てください。
上下の平行移動は加える定数によって変わる
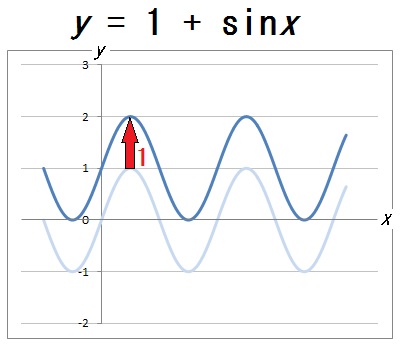
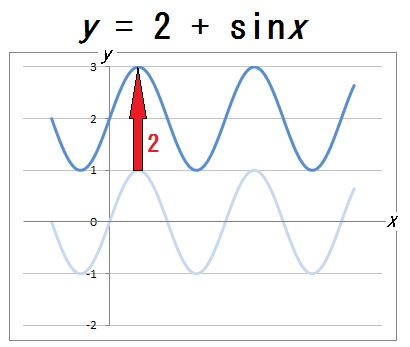
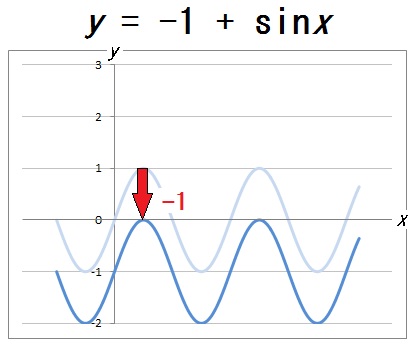
ここから、\(y = c + a\sin bx\) の \(c\) の値をいろいろと変えることで、グラフの上下移動も自由に操れることがわかります。
なお、左右の平行移動についてはフーリエ級数の理解に関係ないので省略します。
![]()
まとめ
$$\large{y = c + a\sin bx}$$
この式において、
\(a\) の値はグラフの振幅を表す
\(b\) の値はグラフの周期を表す
\(c\) の値はグラフの上下平行移動を表す
ということです。
以上の3つは、コサインにおいても当てはまります。
これで三角関数のグラフを自由に変形できるようになりました。
いよいよ次回から、こいつ↓をやっつけていきます。
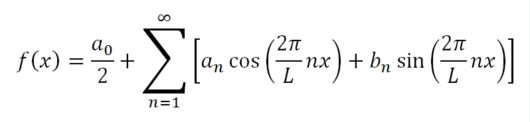
フーリエ級数
乞うご期待!
→三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
≪連載記事一覧≫
- 三角比とはなんだ?何の役に立つ?どんな歴史があるの?
- 三角比はいまどんな職業で役に立っているか?地図製作を例に解説する
- ド文系が「三角比の拡張」と「ラジアン」をわかりやすく解説する
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する①
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する②
- 三角関数は何の役に立つのか?ド文系が「フーリエ級数」まで解説する③(2019/12完結!)



コメント
こんにちは、ニッポン放送は1242kHzです。
したがいまして、今の値より波の数は1000倍、周期は1/1000となります。
ご指摘ありがとうございます。
まちがえてました、記事を訂正しました。